2021-2022学年人教版八年级数学下册 19.2.2 一次函数(1)--图像与性质 课件(共25张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册 19.2.2 一次函数(1)--图像与性质 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 788.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 20:23:13 | ||
图片预览








文档简介
(共25张PPT)
19.2.2 一次函数
学习目标
1.会画一次函数的图象.
2.理解一次函数与正比例函数的概念以及它们的关系.在探究过程中发展抽象思维及概括能力,体验特殊到一般的辩证关系.
3.通过一次函数的图象和性质的研究,体会数形结合在问题解决中的作用,并能应用它们解决相关的问题;
4.能根据一次函数的图象和表达式理解当 k>0 和 k<0 时,图象的变化情况,从而理解一次函数的性质.
学习重难点
重点:
1.了解一次函数、正比例函数的概念及关系,;理解一次函数的图象及性质.
2.会根据已知信息写出一次函数的表达式.
难点:
1.在探索一次函数、正比例函数的过程中发展抽象思维及概括能力.
2.由一次函数的图象归纳出性质以及对性质的理解.
.
复习旧知
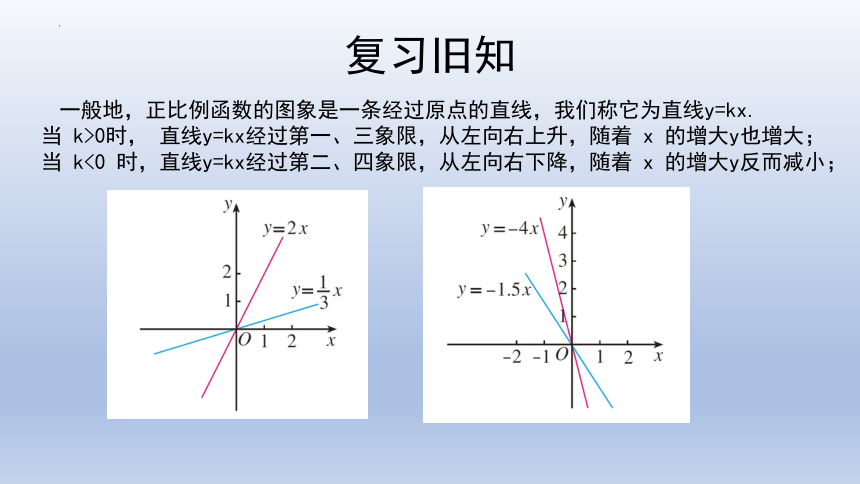
一般地,正比例函数的图象是一条经过原点的直线,我们称它为直线y=kx.
当 k>0时, 直线y=kx经过第一、三象限,从左向右上升,随着 x 的增大y也增大;
当 k<0 时,直线y=kx经过第二、四象限,从左向右下降,随着 x 的增大y反而减小;
情境引入
问题 2:某登山队大本营所在地的气温为5℃,海拔每升高1km气温下降6℃,登山队员由大本营向上登高 x km时,他们所在的位置的气温是y℃,试用解析式表示y与x的关系.
分析:
y随x的变化规律是:从大本营向上当海拔每升高 x km 时,气温从 5℃减少 6x ℃,因此y与x函数解析式为 y=5-6x,这个函数也可以写为 y=-6x+5
当登山队员由大本营向上登高0.5km时,他们所在位置的气温就是当x=0.5时,函数y=-6x+5的值,即y=-6x0.5+5=2(℃)
概念形成
下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式,这些函数解析式有哪些共同特征?
(1)有人发现 ,在 20~25℃时,蟋蟀每分钟鸣叫次数 c 与温度 t(单位: ℃)有关,即 c 的值约是 t 的 7 倍与 35 的差.
(2)一种计算成年人标准体重G(单位:千克)的方法是:以厘米为单位量出身高值 h ,再减常数105,所得差是G的值.
(3)某城市的市内电话的月收费额 y(单位:元)包括月租费 22 元,拨打电话 x min的计时费(按0.1元/min收取).
(4)把一个长10cm、宽5cm的长方形的长减少 x cm,宽不变,长方形的面积 y(单位:cm2)随 x 的变化而变化.
概念形成
正如y=-6x+5一样,上面这些函数都是常数k与自变量的积与常数b的和的形式.
一般地,形如y=kx+b(k、b 是常数,k≠0)的函数,叫做一次函数.当b=0时,y=kx+b即y=kx,所以说正比例函数是一种特殊的一次函数.
(7) ;
1.下列函数中哪些是一次函数,哪些又是正比例函数?
(1) ;
(2) ;
(3) ;
(4) ;
(5) ;
(6) ;
(8) .
应用新知1
一次函数(1)(4)(5)(7)(8)
正比例函数(1)
应用新知1
2.若y=(k﹣2)x|k﹣1|+1表示一次函数,则k等于( )
A.0 B.2 C.0或2 D.﹣2或0
【分析】依据一次函数的定义可知|k﹣1|=1且k﹣2≠0.
【解答】解:∵函数y=(k﹣2)x|k﹣1|+1是一次函数,
∴ |k﹣1|=1
∴ k﹣1=1或k﹣1= ﹣1, k=2或k=0
∵ k﹣2≠0,即k≠2
解得:k=0.
A
正比例函数
解析式 y =kx(k≠0)
性质:k>0,y 随x 的增大而增大;k<0,y 随 x 的增大而减小.
一次函数
解析式 y =kx+b(k≠0)
针对函数 y =kx+b,大家想研究什么?应该怎样研究?
图象:经过原点和
(1,k)的一条直线
y
O
y
O
x
k>0
k<0
x
?
?
知识迁移
研究函数 y =kx+b(k≠0)的性质;
研究方法:
画图象→观察图象→根据变量(坐标)意义分析.
知识迁移
x -2 -1 0 1 2
y=-6x 12 6 0 -6 -12
y=-6x+5 17 11 5 -1 -7
例2 画出函数 y=-6x、y=-6x+5的图象
新知探究
思考:
比较上面两个函数的图象,不难发现,这两个函数的图象形状都是直线,并且倾斜程度相同.函数y=-6x的图象经过原点,函数y=-6x+5的图象与y轴交于点(0,5),即它可以看作由直线y=-6x向上平移5个单位而得到.
小结归纳
比较一次函数y =kx+b(k≠0)与正比例函数y =kx(k≠0)的解析式,容易得出:
一次函数函数y =kx+b(k≠0)的图像可以由直线y =kx平移
个单位长度得到(当b>0时,向上平移;当b<0时,向下平移).一次函数y =kx+b(k≠0)的图像也是一条直线,我们称它为直线y=kx+b.
一次函数性质探究
例3 画出函数y=2x-1与y=-0.5x+1的图象.
一次函数的图象是一条直线→两点确定一条直线→只需取两个点即可
x 0 1
y=2x-1 -1 1
y=-0.5x+1 1 0.5
观察前面一次函数的图象,可以发现规律:
当 k>0 时,y =kx+b.从左到右上升;当 k<0 时,y =kx+b.从左到右下降.
由此可知,一次函数y =kx+b(k,b是常数,k≠0)具有如下性质:
当 k>0 时,y 随 x 的增大而增大;
当 k<0 时,y 随 x 的增大而减小 .
一次函数性质探究
应用新知2
x 0 1
y =x+1 1 2
y =3x+1 1 4
y =-x+1 1 0
y =-3x+1 1 -2
请用简便方法画出下列一次函数的图象:
(1)y =x+1; (2)y =3x+1;
(3)y =-x+1;(4)y =-3x+1
应用新知2
1.请用简便方法画出下列一次函数的图象:
(1)y =x+1; (2)y =3x+1;
(3)y =-x+1;(4)y =-3x+1
思考:
(1)当 k 的符号变化时,函数的增减性怎样变化?
(2)你还从图中发现什么?
应用新知2
2.一次函数y=kx+b的图象如图所示,则一次函数y=bx﹣k的图象所过象限为( )
【分析】根据一次函数y=kx+b的图象经过第一、二、四象限,可以得到k和b的正负,然后根据一次函数的性质,即可得到一次函数y=bx﹣k图象经过哪几个象限,从而可以解答本题.
【解答】解:∵一次函数y=kx+b的图象经过第一、二、四象限,
∴k<0,b>0,
∴b>0,﹣k>0,
∴一次函数y=bx﹣k图象经过第一、二、三象限.
A.一、三、四象限 B.二、三、四象限
C.一、二、三象限 D.一、二、四象限
C
y=kx+b(k≠0)
y=kx(k≠0)
图象
平移
k>0时,直线左低右高,y 随x 的增大而增大;
k<0时,直线左高右低,y 随x 的增大而减小.
两点法画一
次函数图象
研究方法:
画图象→观察图象→根据变量(坐标)意义分析.
课堂小结
课堂小结
x -2 -1 0 1 2
y=-6x 12 6 0 -6 -12
(-2,12) (-1,6) (0,0) (1,6) (2,-12)
y=-6x+5 17 11 5 -1 -7
(-2,17) (-1,11) (0,5) (1,-1) (2,-7)
为什么函数y=-6x+5的图象刚好是由函数y=-6x的图象向上平移5个单位而得到?
问题1
答:若函数y=-6x+5图象上的每一个点都记作(x,y)从列表中可以发现,当x取值相同时,函数y=-6x+5上的对应点可记为(x,y+5),因此y=-6x+5上的每一个点都是由y=-6x图像上的对应点向上平移5个单位得到,所以y=-6x+5的图象可看作由y=-6x的图象向上平移5个单位得到的.同理,y=-6x-5的图象可看作将y=-6x的图象向下平移5个单位.
问题2
一次函数y=kx+b(k≠0),常数k与常数b的取值对函数图象有着怎样的影响?
答:将常数k与常数b的取值对函数图象的影响归纳到表格中.可以看出k值决定着函数图象从左到右是上升还是下降(增减性),b值决定着函数y=kx+b由函数y=kx向上还是向下平移得到(与y轴的交点).
问题3
研究一次函数的性质有什么用?
答:一次函数是一种基本的初等函数,对它性质的研究,在函数解析式与函数图象的相互联系与转化中有着重要作用,这是“数形结合”的思想方法的体现,也是今后进一步研究其它函数的基础.
问题3
研究一次函数的性质有什么用?
生活中的很多现象可以用一次函数模型来刻画,因此,我们通过对一次函数性质的研究,可以对这些现象加以分析、描述,找出其变化规律,还可以帮助人们作出决策来处理其中的问题,把所学的知识应用到生活中去,这也是我们学习数学的目的之一.
问题3
研究一次函数的性质有什么用?
下一节课“一次函数与方程、不等式”从一次函数的角度,对一次方程和不等式进行再认识,揭示函数与之前学习的方程等内容之间的联系.
19.2.2 一次函数
学习目标
1.会画一次函数的图象.
2.理解一次函数与正比例函数的概念以及它们的关系.在探究过程中发展抽象思维及概括能力,体验特殊到一般的辩证关系.
3.通过一次函数的图象和性质的研究,体会数形结合在问题解决中的作用,并能应用它们解决相关的问题;
4.能根据一次函数的图象和表达式理解当 k>0 和 k<0 时,图象的变化情况,从而理解一次函数的性质.
学习重难点
重点:
1.了解一次函数、正比例函数的概念及关系,;理解一次函数的图象及性质.
2.会根据已知信息写出一次函数的表达式.
难点:
1.在探索一次函数、正比例函数的过程中发展抽象思维及概括能力.
2.由一次函数的图象归纳出性质以及对性质的理解.
.
复习旧知
一般地,正比例函数的图象是一条经过原点的直线,我们称它为直线y=kx.
当 k>0时, 直线y=kx经过第一、三象限,从左向右上升,随着 x 的增大y也增大;
当 k<0 时,直线y=kx经过第二、四象限,从左向右下降,随着 x 的增大y反而减小;
情境引入
问题 2:某登山队大本营所在地的气温为5℃,海拔每升高1km气温下降6℃,登山队员由大本营向上登高 x km时,他们所在的位置的气温是y℃,试用解析式表示y与x的关系.
分析:
y随x的变化规律是:从大本营向上当海拔每升高 x km 时,气温从 5℃减少 6x ℃,因此y与x函数解析式为 y=5-6x,这个函数也可以写为 y=-6x+5
当登山队员由大本营向上登高0.5km时,他们所在位置的气温就是当x=0.5时,函数y=-6x+5的值,即y=-6x0.5+5=2(℃)
概念形成
下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式,这些函数解析式有哪些共同特征?
(1)有人发现 ,在 20~25℃时,蟋蟀每分钟鸣叫次数 c 与温度 t(单位: ℃)有关,即 c 的值约是 t 的 7 倍与 35 的差.
(2)一种计算成年人标准体重G(单位:千克)的方法是:以厘米为单位量出身高值 h ,再减常数105,所得差是G的值.
(3)某城市的市内电话的月收费额 y(单位:元)包括月租费 22 元,拨打电话 x min的计时费(按0.1元/min收取).
(4)把一个长10cm、宽5cm的长方形的长减少 x cm,宽不变,长方形的面积 y(单位:cm2)随 x 的变化而变化.
概念形成
正如y=-6x+5一样,上面这些函数都是常数k与自变量的积与常数b的和的形式.
一般地,形如y=kx+b(k、b 是常数,k≠0)的函数,叫做一次函数.当b=0时,y=kx+b即y=kx,所以说正比例函数是一种特殊的一次函数.
(7) ;
1.下列函数中哪些是一次函数,哪些又是正比例函数?
(1) ;
(2) ;
(3) ;
(4) ;
(5) ;
(6) ;
(8) .
应用新知1
一次函数(1)(4)(5)(7)(8)
正比例函数(1)
应用新知1
2.若y=(k﹣2)x|k﹣1|+1表示一次函数,则k等于( )
A.0 B.2 C.0或2 D.﹣2或0
【分析】依据一次函数的定义可知|k﹣1|=1且k﹣2≠0.
【解答】解:∵函数y=(k﹣2)x|k﹣1|+1是一次函数,
∴ |k﹣1|=1
∴ k﹣1=1或k﹣1= ﹣1, k=2或k=0
∵ k﹣2≠0,即k≠2
解得:k=0.
A
正比例函数
解析式 y =kx(k≠0)
性质:k>0,y 随x 的增大而增大;k<0,y 随 x 的增大而减小.
一次函数
解析式 y =kx+b(k≠0)
针对函数 y =kx+b,大家想研究什么?应该怎样研究?
图象:经过原点和
(1,k)的一条直线
y
O
y
O
x
k>0
k<0
x
?
?
知识迁移
研究函数 y =kx+b(k≠0)的性质;
研究方法:
画图象→观察图象→根据变量(坐标)意义分析.
知识迁移
x -2 -1 0 1 2
y=-6x 12 6 0 -6 -12
y=-6x+5 17 11 5 -1 -7
例2 画出函数 y=-6x、y=-6x+5的图象
新知探究
思考:
比较上面两个函数的图象,不难发现,这两个函数的图象形状都是直线,并且倾斜程度相同.函数y=-6x的图象经过原点,函数y=-6x+5的图象与y轴交于点(0,5),即它可以看作由直线y=-6x向上平移5个单位而得到.
小结归纳
比较一次函数y =kx+b(k≠0)与正比例函数y =kx(k≠0)的解析式,容易得出:
一次函数函数y =kx+b(k≠0)的图像可以由直线y =kx平移
个单位长度得到(当b>0时,向上平移;当b<0时,向下平移).一次函数y =kx+b(k≠0)的图像也是一条直线,我们称它为直线y=kx+b.
一次函数性质探究
例3 画出函数y=2x-1与y=-0.5x+1的图象.
一次函数的图象是一条直线→两点确定一条直线→只需取两个点即可
x 0 1
y=2x-1 -1 1
y=-0.5x+1 1 0.5
观察前面一次函数的图象,可以发现规律:
当 k>0 时,y =kx+b.从左到右上升;当 k<0 时,y =kx+b.从左到右下降.
由此可知,一次函数y =kx+b(k,b是常数,k≠0)具有如下性质:
当 k>0 时,y 随 x 的增大而增大;
当 k<0 时,y 随 x 的增大而减小 .
一次函数性质探究
应用新知2
x 0 1
y =x+1 1 2
y =3x+1 1 4
y =-x+1 1 0
y =-3x+1 1 -2
请用简便方法画出下列一次函数的图象:
(1)y =x+1; (2)y =3x+1;
(3)y =-x+1;(4)y =-3x+1
应用新知2
1.请用简便方法画出下列一次函数的图象:
(1)y =x+1; (2)y =3x+1;
(3)y =-x+1;(4)y =-3x+1
思考:
(1)当 k 的符号变化时,函数的增减性怎样变化?
(2)你还从图中发现什么?
应用新知2
2.一次函数y=kx+b的图象如图所示,则一次函数y=bx﹣k的图象所过象限为( )
【分析】根据一次函数y=kx+b的图象经过第一、二、四象限,可以得到k和b的正负,然后根据一次函数的性质,即可得到一次函数y=bx﹣k图象经过哪几个象限,从而可以解答本题.
【解答】解:∵一次函数y=kx+b的图象经过第一、二、四象限,
∴k<0,b>0,
∴b>0,﹣k>0,
∴一次函数y=bx﹣k图象经过第一、二、三象限.
A.一、三、四象限 B.二、三、四象限
C.一、二、三象限 D.一、二、四象限
C
y=kx+b(k≠0)
y=kx(k≠0)
图象
平移
k>0时,直线左低右高,y 随x 的增大而增大;
k<0时,直线左高右低,y 随x 的增大而减小.
两点法画一
次函数图象
研究方法:
画图象→观察图象→根据变量(坐标)意义分析.
课堂小结
课堂小结
x -2 -1 0 1 2
y=-6x 12 6 0 -6 -12
(-2,12) (-1,6) (0,0) (1,6) (2,-12)
y=-6x+5 17 11 5 -1 -7
(-2,17) (-1,11) (0,5) (1,-1) (2,-7)
为什么函数y=-6x+5的图象刚好是由函数y=-6x的图象向上平移5个单位而得到?
问题1
答:若函数y=-6x+5图象上的每一个点都记作(x,y)从列表中可以发现,当x取值相同时,函数y=-6x+5上的对应点可记为(x,y+5),因此y=-6x+5上的每一个点都是由y=-6x图像上的对应点向上平移5个单位得到,所以y=-6x+5的图象可看作由y=-6x的图象向上平移5个单位得到的.同理,y=-6x-5的图象可看作将y=-6x的图象向下平移5个单位.
问题2
一次函数y=kx+b(k≠0),常数k与常数b的取值对函数图象有着怎样的影响?
答:将常数k与常数b的取值对函数图象的影响归纳到表格中.可以看出k值决定着函数图象从左到右是上升还是下降(增减性),b值决定着函数y=kx+b由函数y=kx向上还是向下平移得到(与y轴的交点).
问题3
研究一次函数的性质有什么用?
答:一次函数是一种基本的初等函数,对它性质的研究,在函数解析式与函数图象的相互联系与转化中有着重要作用,这是“数形结合”的思想方法的体现,也是今后进一步研究其它函数的基础.
问题3
研究一次函数的性质有什么用?
生活中的很多现象可以用一次函数模型来刻画,因此,我们通过对一次函数性质的研究,可以对这些现象加以分析、描述,找出其变化规律,还可以帮助人们作出决策来处理其中的问题,把所学的知识应用到生活中去,这也是我们学习数学的目的之一.
问题3
研究一次函数的性质有什么用?
下一节课“一次函数与方程、不等式”从一次函数的角度,对一次方程和不等式进行再认识,揭示函数与之前学习的方程等内容之间的联系.
