2021--2022学年华东师大版七年级数学下册 8.2解一元一次不等式 课件(共23张PPT)
文档属性
| 名称 | 2021--2022学年华东师大版七年级数学下册 8.2解一元一次不等式 课件(共23张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
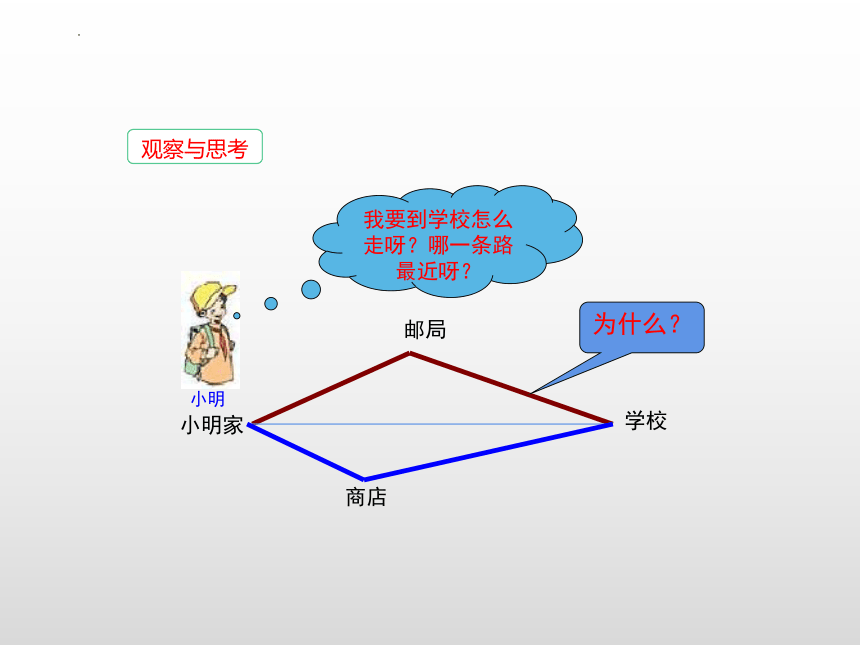
观察与思考
小明
我要到学校怎么走呀?哪一条路最近呀?
为什么?
邮局
学校
商店
小明家
三角形的三边关系
华师大版七年级数学下册
学习目标
1.探索并掌握三角形的三边关系;
2.会运用三角形的三边关系解决实际应用问题;
3.了解三角形的稳定性.
一.探究新知(一)
读一读、画一画
画一个三角形,使它的三条边长分别为4cm、3cm、2.5cm.
作法:1、画线段AB=4cm;
2、以点A为圆心、3cm长为半径画圆弧,再以点B为圆心、2.5CM长为半径画圆弧,两弧相交于点C;
3、连结AC、BC;
则△ABC就是所画的三角形.
(活动一)
(活动二)
现有若干条已知长度的线段:三条长2cm、三条长3cm、两条长4cm、两条长5cm、两条长6cm.
问题
任意选择三条线段画三角形,你能画出来吗?
活动记录
组别 所选的三边长 能否画出三角形
1 2,2,4
2 2,3,6
3 4,5,6
2
2
4
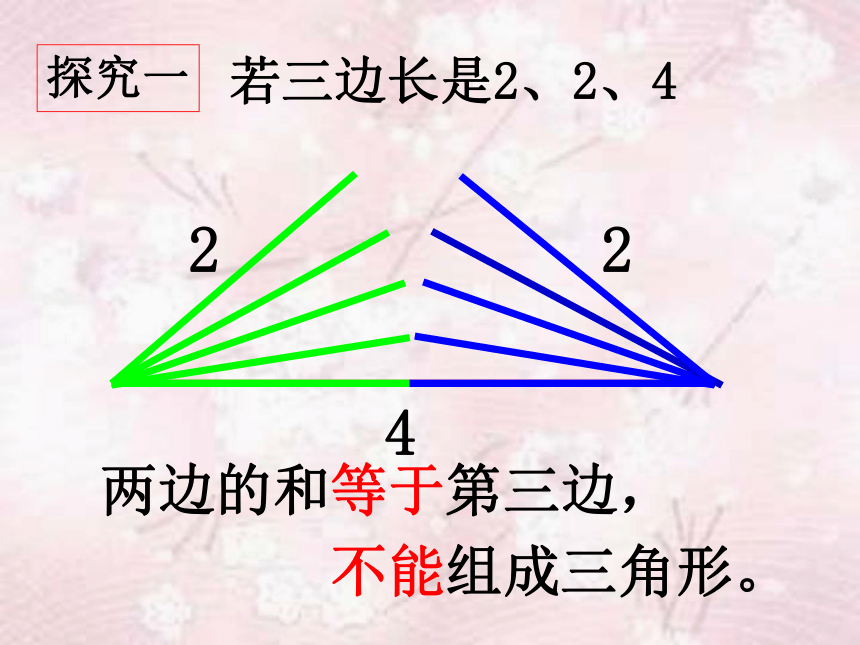
若三边长是2、2、4
探究一
两边的和等于第三边,
不能组成三角形。
两边的和小于第三边,
不能组成三角形。
2
3
6
若三边长是2、3、6
4
5
6
两边的和大于第三边,
能组成三角形。
若三边长是4、5、6
三角形的任何两边的和大于第三边.
三角形的三边关系:
a
b
A
B
C
c
即:△ABC中
a+b>c
b+c>a
c+a>b
探究二
探究三
△ABC中,
a+b>c
b+c>a
c+a>b
a>c-b
b>a-c
c>b-a
三角形的任何两边的差小于第三边.
a
b
A
B
C
c
以长度为6cm、4cm、3cm 的三条线段能否组成一个三角形?
想一想:你有更简便的方法吗?
二.新知应用
若较小的两条线段之和大于第三条线段,便可组成三角形;
若不满足,则不能组成三角形.
如何判断三条已知线段能否组成三角形?
归纳总结
1.下列各组线段能围成三角形吗?
1、4cm ,9cm, 5cm ( )
×
2、8cm ,7cm, 6cm ( )
√
3、3cm ,10cm, 5cm ( )
×
练一练:
2.一木工有两根长分别是40cm和60cm 的木条,要另找一根木条,钉成一个三角木架,问第三根木条的长度应在什么范围内?
60-40< L < 40+60
已知等腰三角形两条边长分别为3cm、5cm,求等腰三角形的周长.
三.拓展练习
解:①若腰长是3cm,
周长是:3+3+5=11cm;
②若腰长是5cm,
周长是:5+5+3=13cm.
∴等腰三角形的周长是11cm或13cm.
探究新知(二)
木工小组的同学在修理桌椅时,常常在桌椅下边斜着钉一根木条。他们这样做是为什么?
利用三角形的稳定性,使桌椅更牢固。
泥阳初中数学组
三角形的稳定性
定义:
如果三角形的三条边固定,那么三角形的形状和大小就完全确定了。
三角形在现实生活中应用:
四.小结深化
通过本节课的学习,
你有哪些收获?
我学会了
1、三角形的三边关系定理:
任何两边之和大于第三边
任何两边的差小于第三边
2、三角形第三边的取值范围:
两边之差<第三边 < 两边之和
3.三角形具有稳定性
五.作业设计
1:教科书习题9.1第2、4题。
2:思考题
从中任选三条,一共有多少组?能组成三角形的有几组?
三条长2cm、三条长3cm、两条长4cm、两条长5cm、两条长6cm.
谢谢指导!
观察与思考
小明
我要到学校怎么走呀?哪一条路最近呀?
为什么?
邮局
学校
商店
小明家
三角形的三边关系
华师大版七年级数学下册
学习目标
1.探索并掌握三角形的三边关系;
2.会运用三角形的三边关系解决实际应用问题;
3.了解三角形的稳定性.
一.探究新知(一)
读一读、画一画
画一个三角形,使它的三条边长分别为4cm、3cm、2.5cm.
作法:1、画线段AB=4cm;
2、以点A为圆心、3cm长为半径画圆弧,再以点B为圆心、2.5CM长为半径画圆弧,两弧相交于点C;
3、连结AC、BC;
则△ABC就是所画的三角形.
(活动一)
(活动二)
现有若干条已知长度的线段:三条长2cm、三条长3cm、两条长4cm、两条长5cm、两条长6cm.
问题
任意选择三条线段画三角形,你能画出来吗?
活动记录
组别 所选的三边长 能否画出三角形
1 2,2,4
2 2,3,6
3 4,5,6
2
2
4
若三边长是2、2、4
探究一
两边的和等于第三边,
不能组成三角形。
两边的和小于第三边,
不能组成三角形。
2
3
6
若三边长是2、3、6
4
5
6
两边的和大于第三边,
能组成三角形。
若三边长是4、5、6
三角形的任何两边的和大于第三边.
三角形的三边关系:
a
b
A
B
C
c
即:△ABC中
a+b>c
b+c>a
c+a>b
探究二
探究三
△ABC中,
a+b>c
b+c>a
c+a>b
a>c-b
b>a-c
c>b-a
三角形的任何两边的差小于第三边.
a
b
A
B
C
c
以长度为6cm、4cm、3cm 的三条线段能否组成一个三角形?
想一想:你有更简便的方法吗?
二.新知应用
若较小的两条线段之和大于第三条线段,便可组成三角形;
若不满足,则不能组成三角形.
如何判断三条已知线段能否组成三角形?
归纳总结
1.下列各组线段能围成三角形吗?
1、4cm ,9cm, 5cm ( )
×
2、8cm ,7cm, 6cm ( )
√
3、3cm ,10cm, 5cm ( )
×
练一练:
2.一木工有两根长分别是40cm和60cm 的木条,要另找一根木条,钉成一个三角木架,问第三根木条的长度应在什么范围内?
60-40< L < 40+60
已知等腰三角形两条边长分别为3cm、5cm,求等腰三角形的周长.
三.拓展练习
解:①若腰长是3cm,
周长是:3+3+5=11cm;
②若腰长是5cm,
周长是:5+5+3=13cm.
∴等腰三角形的周长是11cm或13cm.
探究新知(二)
木工小组的同学在修理桌椅时,常常在桌椅下边斜着钉一根木条。他们这样做是为什么?
利用三角形的稳定性,使桌椅更牢固。
泥阳初中数学组
三角形的稳定性
定义:
如果三角形的三条边固定,那么三角形的形状和大小就完全确定了。
三角形在现实生活中应用:
四.小结深化
通过本节课的学习,
你有哪些收获?
我学会了
1、三角形的三边关系定理:
任何两边之和大于第三边
任何两边的差小于第三边
2、三角形第三边的取值范围:
两边之差<第三边 < 两边之和
3.三角形具有稳定性
五.作业设计
1:教科书习题9.1第2、4题。
2:思考题
从中任选三条,一共有多少组?能组成三角形的有几组?
三条长2cm、三条长3cm、两条长4cm、两条长5cm、两条长6cm.
谢谢指导!
