2021-2022学年青岛版八年级数学下册 11.1 图形的平移 课件(共23张PPT)
文档属性
| 名称 | 2021-2022学年青岛版八年级数学下册 11.1 图形的平移 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 19.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
11.1 图形的平移
八年级数学
第11章 图形的平移与旋转
1、理解平移的概念及决定因素.
2、会找出平移前后图形中对应点、对应角
和对应线段.
3、掌握平移的性质及其运用.
学习目标:
课堂导入:
公路上奔驰的汽车
天上飞着的飞机
想一想:这些图形的形状、大小在运动前后是否发生了改变
知识点1: 平移的相关概念
新知探究
在平面内,把一个图形整体沿某一直线方向移动,会得到一个新的图形,图形的这种移动,叫做平移.
平移前后能重合的点叫对应点
注意:图形的平移是一种位置变换,平移只改变图形的位置,不改变图形的形状和大小.
观察以下几种移动,想一想平移有什么要素?
平移的要素:1. 平移的方向;2. 平移的距离.
注意:图形平移的方向可以是任意指定的方向,不限于是水平的或竖直的,但必须是直线方向.
平移后的位置由平移的方向和平移的距离确定。
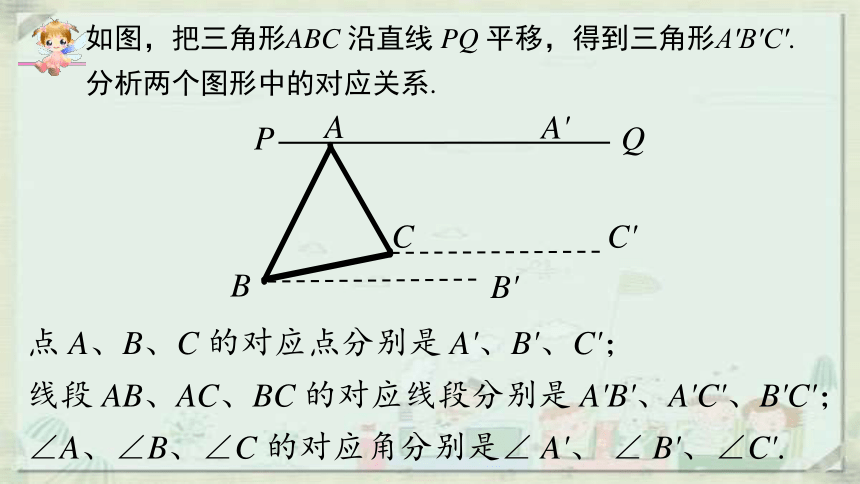
点 A、B、C 的对应点分别是 A'、B'、C';
线段 AB、AC、BC 的对应线段分别是 A'B'、A'C'、B'C';
∠A、∠B、∠C 的对应角分别是∠ A'、 ∠ B'、∠C'.
如图,把三角形ABC 沿直线 PQ 平移,得到三角形A′B′C′. 分析两个图形中的对应关系.
B'
C'
A'
A
B
C
P
Q
图形的平移是整个图形都在移动,即图形中所有点、线平移的方向和平移的距离都相同,所以确定一个图形平移的方向和距离,只需确定图形上一个点平移的方向和距离即可.
A(A`)
C`
A`
B`
L(L`)
B(B`)
C(C`)
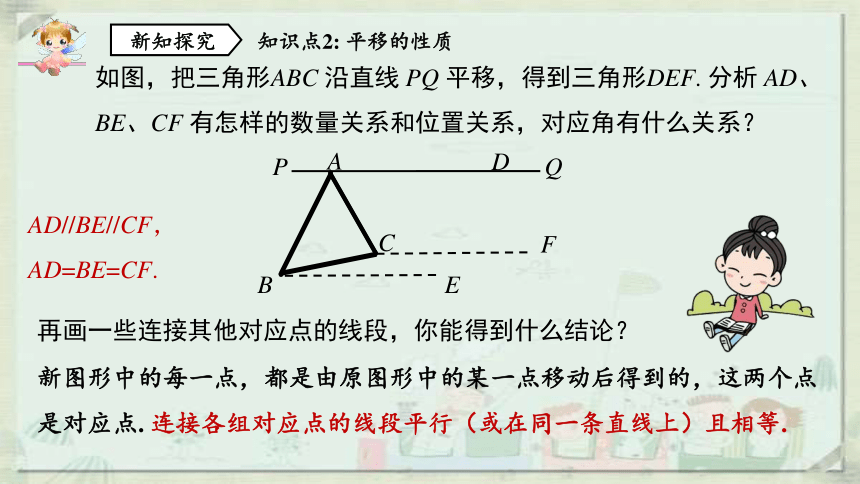
如图,把三角形ABC 沿直线 PQ 平移,得到三角形DEF. 分析 AD、BE、CF 有怎样的数量关系和位置关系,对应角有什么关系?
F
D
A
B
C
P
Q
E
AD//BE//CF, AD=BE=CF.
再画一些连接其他对应点的线段,你能得到什么结论?
知识点2: 平移的性质
新知探究
新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点. 连接各组对应点的线段平行(或在同一条直线上)且相等.
F
D
A
B
C
P
Q
E
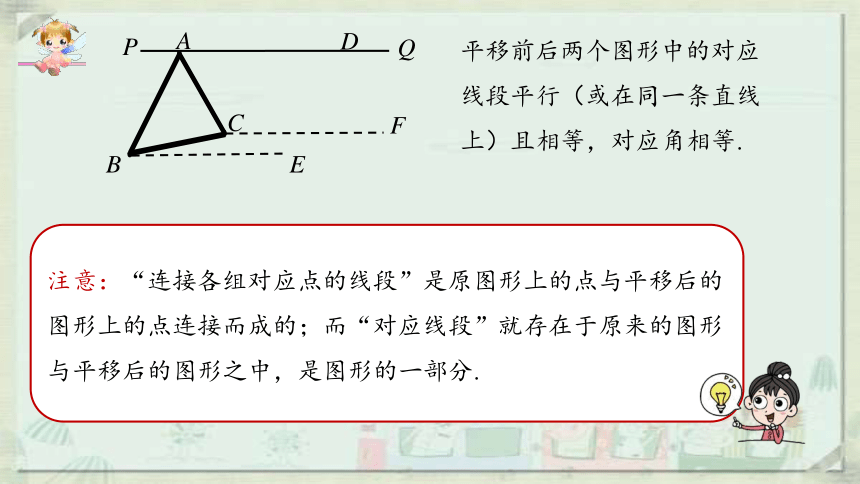
平移前后两个图形中的对应线段平行(或在同一条直线上)且相等,对应角相等.
注意:“连接各组对应点的线段”是原图形上的点与平移后的图形上的点连接而成的;而“对应线段”就存在于原来的图形与平移后的图形之中,是图形的一部分.
平移的性质
1. 平移后得到的新图形与原图形的形状、大小完全相同;
2. 连接各组对应点的线段平行(或在同一条直线上)且相等.
3. 平移前后两个图形中的对应线段平行(或在同一条直线上)且相等,对应角相等.
归纳总结:
如图所示,平移三角形 ABC ,使点 C 移动到点 C'. 画出平移后的三角形 A'B'C' .
A
B
C
(1) 连接 CC';
(2) 分别过点 A,B 按射线 CC' 的方向作线段 BB',AA',使得它们与线段 CC' 平行且相等;
(3) 连接 A'C',A'B',B'C',三角形 A'B'C' 为所求.
知识点3: 平移作图
新知探究
要正确画出一个图形按要求平移后的新图形,只要先画出关键点的对应点,如线段的端点、三角形的顶点、圆的圆心等等,就很容易画出新图形了
1. 定:确定平移的方向和距离;
2. 找:找出确定图形形状的关键点;
3. 移:按平移的方向和距离平移各个关键点,得到各个关键点的对应点;
4. 连:按原图形的顺序依次连接各对应点;
5. 写:写出结论.
平移作图的基本步骤
例1 画出点A沿着线段PQ的方向平移到点A′的位置,平移的距离是线段PQ的长度;
P
Q
A
A′
归纳总结:
例2 画出线段AB沿着线段MN的方向平移到A′B′的位置,平移的距离是3cm;
M
N
A
B
A′
B′
例3 画出△ABC沿着线段MN的方向平移后的位置,平移的距离是线段MN的长度;
N
M
B
A
C
1. 平移的性质是平移作图的依据.
2. 确定一个图形平移后的位置需三个条件:
① 图形原来的位置;
② 平移的方向;
③ 平移的距离.
这三个条件缺一不可,只有这样,平移后的图形才唯一确定.
归纳总结:
1.将点A分别向上、向下、向左、向右平移5个单位长度,所得到的点的坐标分
别是( ,)( , )( ,)( , )
阅读课本169—171页交流与发现,完成下列问题
y
1 2 3 4 5 6
-6
7
6
5
4
2
3
1
-1
-2
-3
-4
-5
-6
-7
-5
-4
-3
-2
-1
x
6
7
6
7
6
7
6
7
-1
-1
-1
-5
-1
0
●
A(-2,1)
●
A1(-2,6)
●
A2(-2,-4)
●
A4(3,1)
●
A3(-7,1)
-7
2.将点A向右平移5个单位长度,再向上平移3个单位长度得到点B,请你在坐标系中标出点B的位置,它坐标是( , )
y
1 2 3 4 5 6
-6
7
6
5
4
2
3
1
-1
-2
-3
-4
-5
-6
-7
-5
-4
-3
-2
-1
x
6
7
6
7
6
7
6
7
-1
-1
-1
-5
-1
0
●
A(-2,1)
●
B(3,4)
●
(3,1)
-7
●
●
●
3.将点A向右平移2个单位长度,再向下平移4个单位长度得到点C,请你在坐标系中标出点C的位置,它坐标是( , )
y
1 2 3 4 5 6
-6
7
6
5
4
2
3
1
-1
-2
-3
-4
-5
-6
-7
-5
-4
-3
-2
-1
x
6
7
6
7
6
7
6
7
-1
-1
-1
-5
-1
0
●
A(-2,1)
C(0,-3)
(0,1)
-7
5.如果将点A向左平移h个单位长度,再向下平移k个单位长度得到点D,那么点D坐标是( , )
4.把点A(-2,1)进行怎样的平移可以得到点E ( , )
E ( 5 , -4 )
●
向右平移
a个单位
向左平移
a个单位
归纳
P(x, y)
P(x-a, y)
P(x+a, y)
向上平移
个单位
b
P(x, y+b)
向下平移
个单位
b
P(x, y-b)
左减
右加
上加
下减
1.下面各组图形中,能由其中一个图形经过平移得到另一个图形的是( )
A
跟踪训练
大小不同
旋转
轴对称
2.如图,将面积为 3 的三角形 ABC 沿 BC 方向平移到三角形 DEF 的位置,CE =5,EF =2,∠B=40°,则
(1) BC = ,∠DEF = .
(2) 平移的距离是______,三角形 DEF 的面积是 .
2
40°
7
3
EF
∠B
CF
CE+EF=7
3.如图,将三角形ABC 向右平移得到三角形DEF,已知 A,D 两点的距离为 1,CE=2,则 BF 的长为( )
A.5 B.4 C.3 D.2
B
B
E
C
F
A
D
平移距离BE=CF=1
BF=BE+EC+CF=4
4.(2021 鞍山中考)如图,三角形 ABC 沿 BC 所在直线向右平移得到三角形 DEF,已知 EC=2,BF=8,则平移的距离为 .
3
B
E
C
F
A
D
BE+CF=82=6
BE=CF
BE=CF=3
5.如图,将直角三角形 ABC 沿 CB 方向平移得到直角三角形 DEF,已知∠ABC =90°,AG =2,BE =4,DE =6,求阴影部分的面积.
解:由平移得:AB =DE =6,S三角形DEF=S三角形ABC,
∴ BG =ABAG=62=4,
∴ S阴影部分=S梯形BEDG= (BG+DE)·BE= ×(4+6)×4=20.
6.如图,在网格中,每个小正方形的边长均为 1 个单位长度.我们将小正方形的顶点叫做格点,三角形 ABC 的三个顶点均在格点上.将三角形 ABC 先向右平移 6 个单位长度,再向上平移 3 个
单位长度,得到三角形
A1B1C1,画出平移后的
三角形A1B1C1.
A
B
C
A1
B1
C1
平移
概念
两要素
性质
作图
平移的方向、平移的距离
平移前后图形的形状和大小完全相同
对应线段平行(或在同一直线上)且相等
对应点所连线段平行(或在同一直线上)且相等
课堂小结
一定、二找、三移、四连、五写
11.1 图形的平移
八年级数学
第11章 图形的平移与旋转
1、理解平移的概念及决定因素.
2、会找出平移前后图形中对应点、对应角
和对应线段.
3、掌握平移的性质及其运用.
学习目标:
课堂导入:
公路上奔驰的汽车
天上飞着的飞机
想一想:这些图形的形状、大小在运动前后是否发生了改变
知识点1: 平移的相关概念
新知探究
在平面内,把一个图形整体沿某一直线方向移动,会得到一个新的图形,图形的这种移动,叫做平移.
平移前后能重合的点叫对应点
注意:图形的平移是一种位置变换,平移只改变图形的位置,不改变图形的形状和大小.
观察以下几种移动,想一想平移有什么要素?
平移的要素:1. 平移的方向;2. 平移的距离.
注意:图形平移的方向可以是任意指定的方向,不限于是水平的或竖直的,但必须是直线方向.
平移后的位置由平移的方向和平移的距离确定。
点 A、B、C 的对应点分别是 A'、B'、C';
线段 AB、AC、BC 的对应线段分别是 A'B'、A'C'、B'C';
∠A、∠B、∠C 的对应角分别是∠ A'、 ∠ B'、∠C'.
如图,把三角形ABC 沿直线 PQ 平移,得到三角形A′B′C′. 分析两个图形中的对应关系.
B'
C'
A'
A
B
C
P
Q
图形的平移是整个图形都在移动,即图形中所有点、线平移的方向和平移的距离都相同,所以确定一个图形平移的方向和距离,只需确定图形上一个点平移的方向和距离即可.
A(A`)
C`
A`
B`
L(L`)
B(B`)
C(C`)
如图,把三角形ABC 沿直线 PQ 平移,得到三角形DEF. 分析 AD、BE、CF 有怎样的数量关系和位置关系,对应角有什么关系?
F
D
A
B
C
P
Q
E
AD//BE//CF, AD=BE=CF.
再画一些连接其他对应点的线段,你能得到什么结论?
知识点2: 平移的性质
新知探究
新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点. 连接各组对应点的线段平行(或在同一条直线上)且相等.
F
D
A
B
C
P
Q
E
平移前后两个图形中的对应线段平行(或在同一条直线上)且相等,对应角相等.
注意:“连接各组对应点的线段”是原图形上的点与平移后的图形上的点连接而成的;而“对应线段”就存在于原来的图形与平移后的图形之中,是图形的一部分.
平移的性质
1. 平移后得到的新图形与原图形的形状、大小完全相同;
2. 连接各组对应点的线段平行(或在同一条直线上)且相等.
3. 平移前后两个图形中的对应线段平行(或在同一条直线上)且相等,对应角相等.
归纳总结:
如图所示,平移三角形 ABC ,使点 C 移动到点 C'. 画出平移后的三角形 A'B'C' .
A
B
C
(1) 连接 CC';
(2) 分别过点 A,B 按射线 CC' 的方向作线段 BB',AA',使得它们与线段 CC' 平行且相等;
(3) 连接 A'C',A'B',B'C',三角形 A'B'C' 为所求.
知识点3: 平移作图
新知探究
要正确画出一个图形按要求平移后的新图形,只要先画出关键点的对应点,如线段的端点、三角形的顶点、圆的圆心等等,就很容易画出新图形了
1. 定:确定平移的方向和距离;
2. 找:找出确定图形形状的关键点;
3. 移:按平移的方向和距离平移各个关键点,得到各个关键点的对应点;
4. 连:按原图形的顺序依次连接各对应点;
5. 写:写出结论.
平移作图的基本步骤
例1 画出点A沿着线段PQ的方向平移到点A′的位置,平移的距离是线段PQ的长度;
P
Q
A
A′
归纳总结:
例2 画出线段AB沿着线段MN的方向平移到A′B′的位置,平移的距离是3cm;
M
N
A
B
A′
B′
例3 画出△ABC沿着线段MN的方向平移后的位置,平移的距离是线段MN的长度;
N
M
B
A
C
1. 平移的性质是平移作图的依据.
2. 确定一个图形平移后的位置需三个条件:
① 图形原来的位置;
② 平移的方向;
③ 平移的距离.
这三个条件缺一不可,只有这样,平移后的图形才唯一确定.
归纳总结:
1.将点A分别向上、向下、向左、向右平移5个单位长度,所得到的点的坐标分
别是( ,)( , )( ,)( , )
阅读课本169—171页交流与发现,完成下列问题
y
1 2 3 4 5 6
-6
7
6
5
4
2
3
1
-1
-2
-3
-4
-5
-6
-7
-5
-4
-3
-2
-1
x
6
7
6
7
6
7
6
7
-1
-1
-1
-5
-1
0
●
A(-2,1)
●
A1(-2,6)
●
A2(-2,-4)
●
A4(3,1)
●
A3(-7,1)
-7
2.将点A向右平移5个单位长度,再向上平移3个单位长度得到点B,请你在坐标系中标出点B的位置,它坐标是( , )
y
1 2 3 4 5 6
-6
7
6
5
4
2
3
1
-1
-2
-3
-4
-5
-6
-7
-5
-4
-3
-2
-1
x
6
7
6
7
6
7
6
7
-1
-1
-1
-5
-1
0
●
A(-2,1)
●
B(3,4)
●
(3,1)
-7
●
●
●
3.将点A向右平移2个单位长度,再向下平移4个单位长度得到点C,请你在坐标系中标出点C的位置,它坐标是( , )
y
1 2 3 4 5 6
-6
7
6
5
4
2
3
1
-1
-2
-3
-4
-5
-6
-7
-5
-4
-3
-2
-1
x
6
7
6
7
6
7
6
7
-1
-1
-1
-5
-1
0
●
A(-2,1)
C(0,-3)
(0,1)
-7
5.如果将点A向左平移h个单位长度,再向下平移k个单位长度得到点D,那么点D坐标是( , )
4.把点A(-2,1)进行怎样的平移可以得到点E ( , )
E ( 5 , -4 )
●
向右平移
a个单位
向左平移
a个单位
归纳
P(x, y)
P(x-a, y)
P(x+a, y)
向上平移
个单位
b
P(x, y+b)
向下平移
个单位
b
P(x, y-b)
左减
右加
上加
下减
1.下面各组图形中,能由其中一个图形经过平移得到另一个图形的是( )
A
跟踪训练
大小不同
旋转
轴对称
2.如图,将面积为 3 的三角形 ABC 沿 BC 方向平移到三角形 DEF 的位置,CE =5,EF =2,∠B=40°,则
(1) BC = ,∠DEF = .
(2) 平移的距离是______,三角形 DEF 的面积是 .
2
40°
7
3
EF
∠B
CF
CE+EF=7
3.如图,将三角形ABC 向右平移得到三角形DEF,已知 A,D 两点的距离为 1,CE=2,则 BF 的长为( )
A.5 B.4 C.3 D.2
B
B
E
C
F
A
D
平移距离BE=CF=1
BF=BE+EC+CF=4
4.(2021 鞍山中考)如图,三角形 ABC 沿 BC 所在直线向右平移得到三角形 DEF,已知 EC=2,BF=8,则平移的距离为 .
3
B
E
C
F
A
D
BE+CF=82=6
BE=CF
BE=CF=3
5.如图,将直角三角形 ABC 沿 CB 方向平移得到直角三角形 DEF,已知∠ABC =90°,AG =2,BE =4,DE =6,求阴影部分的面积.
解:由平移得:AB =DE =6,S三角形DEF=S三角形ABC,
∴ BG =ABAG=62=4,
∴ S阴影部分=S梯形BEDG= (BG+DE)·BE= ×(4+6)×4=20.
6.如图,在网格中,每个小正方形的边长均为 1 个单位长度.我们将小正方形的顶点叫做格点,三角形 ABC 的三个顶点均在格点上.将三角形 ABC 先向右平移 6 个单位长度,再向上平移 3 个
单位长度,得到三角形
A1B1C1,画出平移后的
三角形A1B1C1.
A
B
C
A1
B1
C1
平移
概念
两要素
性质
作图
平移的方向、平移的距离
平移前后图形的形状和大小完全相同
对应线段平行(或在同一直线上)且相等
对应点所连线段平行(或在同一直线上)且相等
课堂小结
一定、二找、三移、四连、五写
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
