第三讲 整数、小数、分数、百分数的运算
图片预览


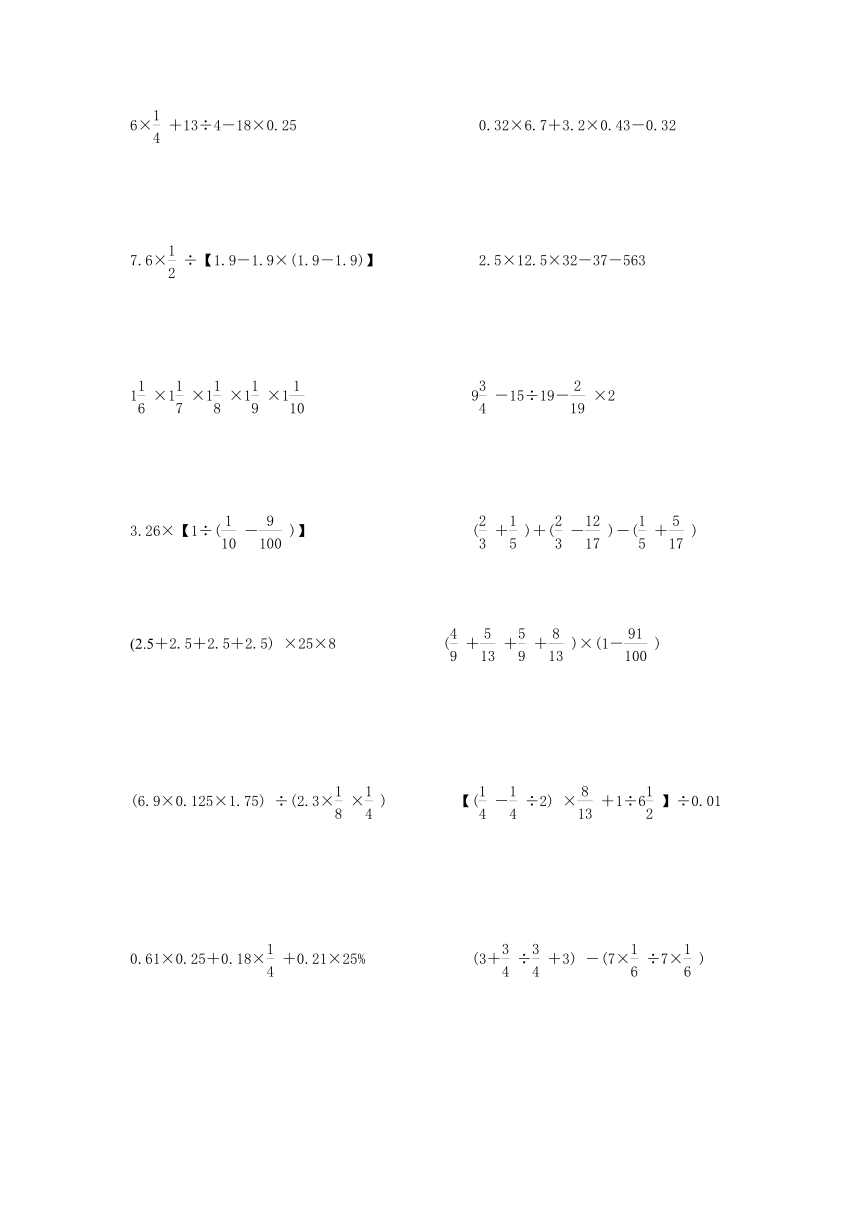


文档简介
第三讲 整数、小数、分数、百分数的运算
知识点一 四则运算的意义
整数加法、小数加法、分数加法的意义:把两个数合成一个数的运算
整数减法、小数减法、分数减法的意义:已知两个数的和与其中的一个加数,求另一个加数的运算
整数乘法的意义:求几个相同加数的和的简便运算
小数乘法的意义:小数乘整数与整数乘法的意义相同;一个数乘小数,就是求这个数的十分之几、百分之几……是多少。
整数乘分数的意义:一个数乘分数,就是求这个数的几分之几是多少
分数乘整数的意义:分数乘整数,就是求几个相同分数的和的简便运算
整数除法、小数除法、分数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。
知识点二 四则运算的计算方法
1、加减法的计算方法
(1)整数的加法:相同数位对齐,从低位加起,哪一位上的数相加满十,就要向前一位进一。
(2)整数的减法:相同数位对齐,从低位减起,哪一位上的数不够减要从前一位上退一,在本位上加上10再减。
(3)小数的加减法:计算小数加减法时,先把小数点对齐(也就是相同的数位对齐),再按照整数加减法的法则进行计算,最后在得数里对齐横线上的小数点,点上小数点
(4)分数的加减法:同分母的分数相加减,分母不变,只把分子相加减;异分母的分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
2、乘法的计算方法
(1)整数的乘法:从低位到高位分别用因数的每一位去乘另一个因数;用一个因数的哪一位去乘,求得的数的末位就要和那一位对齐;然后把几次求得的积加起来
(2)小数乘法:先按照整数乘法的法则算出积,再看因数中一共有几位小数,就从积的右边起数出几位点上小数点
(3)分数乘法:分数乘整数,用分数的分子和整数相乘的积作分子,分母不变;分数乘分数,用分子相乘的积作分子,分母相乘的积作分母。
3、除法的计算方法
(1)整数的除法:从被除数的高位除起,除数有几位就先看被除数的前几位,如果前几位比除数小,就多取一位再除,除到哪一位,商就写在那一位的上面;每次除得的余数必须比除数小;在求出商的最高位以后,如果被除数的哪一位上不够商1,就在那一位上写0
(2)小数除法:除数是整数时,按照整数除法进行计算,商的小数点要与被除数的小数点对齐。除数是小数时,要先把除数转化成整数,同时把被除数扩大相同的倍数,然后按照除数是整数的除法进行计算。
(3)分数的除法:甲数除以乙数(0除外),等于甲数乘乙数的倒数。
知识点三 整数四则运算中各部分间的关系
1、加法:和=加数+加数 加数=和-另一个加数
2、减法:差=被减数-减数 减数=被减数-差 被减数=减数+差
3、乘法:积=因数×因数 一个因数=积÷另一个因数
4、除法:商=被除数÷除数 除数=被除数÷商 被除数=除数×商
知识点四 四则运算的估算方法
根据算式中各数的特点,估算时一般是将其中的大数看作整十、整百、整千……的数,使原式通过口算便可求出得数。由于得数是近似值,所以计算时要用≈连接
知识点五 四则运算定律、运算性质
1、运算定律
(1)加法结合律:两个数相加,交换加数的位置,它们的和不变 a+b=b+a
(2)加法结合律:三个数相加,先把前两个数相加,再加上第三个数,或者先把后面两个数相加,再和第一个相加,它们的和不变。a+b+c=(a+b)+c=a+(b+c)
(3)乘法交换律: 两个数相乘,交换因数的位置,它们的积不变。a×b=b×a
(4)乘法结合律:三个数相乘,先把前两个数相乘,再乘第三个数,或者先把后面两个数相乘,再和第一个数相乘,它们的积不变。a×b×c=(a×b) ×c=a×(b×c)
(5)乘法分配律:两个数的和与一个数相乘,等于把这两个数分别与这个数相乘,再把两个积加起来。(a+b) ×c=a×c+b×c a×(b+c)=a×b+a×c
2、运算性质
(1)减法的运算性质:a-(b+c)=a-b-c a-(b-c)=a-b+c
(2)除法的运算性质(除数不为0):
a÷(b×c)=a÷b÷c a÷(b÷c)=a÷b×c
(a+b)÷c=a÷c+b÷c (a-b) ÷c=a÷c-b÷c
知识点六 四则混合运算的顺序
四则运算分为两级:加法和减法叫做第一级运算;乘法和除法叫做第二级运算。
(1)在没有括号的算式里,如果只含有同一级运算,要从左往右依次计算;如果含有两级运算,要先做第二级运算,再做第一级运算。
(2)在有括号的算式里,要先算小括号里面的,再算中括号里面的,最后算括号外面的。
疯狂操练一
(8+3)-( - ) 13.76-(+1.76+1)
(×)×(13×18) 19.98×37-199.8×1.9+1998×0.82
35.2÷9+35.2÷ 0.25×1.25×320
6×+13÷4-18×0.25 0.32×6.7+3.2×0.43-0.32
7.6×÷【1.9-1.9×(1.9-1.9)】 2.5×12.5×32-37-563
1×1×1×1×1 9-15÷19-×2
3.26×【1÷(-)】 (+)+(-)-(+)
(2.5+2.5+2.5+2.5) ×25×8 (+++)×(1-)
(6.9×0.125×1.75) ÷(2.3××) 【(-÷2) ×+1÷6】÷0.01
0.61×0.25+0.18×+0.21×25% (3+÷+3) -(7×÷7×)
【5-(0.5×9+×)】÷ (12+) ×2.5+(9+10)× 2
1×【7+(4.125-)-4】 5-【1-(2.5-1)】÷0.125
1000÷32÷0.25÷1.25
知识点七 简便运算一
专题简析:
根据算式的结构和数的特征,灵活运用运算法则、定律、性质和某些公式,可以把一些较复杂的四则混合运算化繁为简,化难为易。
例题1
计算:4.75-9.63+(8.25-1.37)
疯狂操练1
计算下面各题:
1、6.73-2+(3.27-1) 2、
3、14.15-()-2.125 4、
例题2
计算:36×1.09+1.2×67.3
疯狂操练2
计算:
1、45×2.08+1.5×37.6 2、52×11.1+2.6×778
3、48×1.08+1.2×56.8 4、72×2.09-1.8×73.6
例题3
计算:333387
疯狂操练3
计算下面各题:
1、 2、
3、 4、
例题4
计算:
疯狂操练4
计算下面各题:
1、 2、
3、
例题5
计算:81.5×15.8+81.5×51.8+67.6×18.5
疯狂操练5
1、53.5×35.3+53.5×43.2+78.5×46.5
2、235×12.1+235×42.2-135×54.3
3、3.75×735-×5730+16.2×62.5
例题6
计算:
疯狂操练6
计算下面各题:
1、99999×77778+33333×66666 2、34.5×76.5-345×6.42-123×1.45
3、77×13+255×999+510
知识点八 简便运算二
专题简析:
在进行分数运算时,除了牢记运算定律、性质外,还要仔细审题,仔细观察运算符号和数字特点,合理地把参加运算的数拆开或者合并进行重新组合,使其变成符合运算定律的模式,以便于口算,从而简化运算。
在后面的四个例题中,将着重向同学们介绍怎样用拆分法(也叫裂项法、拆项法)进行分数的简便运算。运用拆分法解题主要是使拆开后的一些分数互相抵消,达到简化运算的目的。一般地,形如的分数可以拆成;形如的分数可以拆成;形如的分数可以拆成等等。同学们可以结合例题思考其中的规律。
例题1
计算:(1) (2)
疯狂操练1
用简便方法计算下面各题:
1、×8 2、×126 3、35×
4、73× 5、×1999
例题2
计算:73×
疯狂操练2
计算下面各题:
1、64× 2、22×
3、×57 4、41×+51×
例题3
计算:
疯狂操练3
计算下面各题:
1、×39+×27 2、×35+×17
3、×5+×5+×10
例题4
计算:
疯狂操练4
计算下面各题:
1、 2、
3、 4、
例题5
计算:
疯狂操练5
计算下面各题:
1、
2、
3、
4、
例题6
计算
疯狂操练6
计算下面各题:
1、
2、+++……+
3、
4、++++
例题7
计算:
疯狂操练7
计算下面各题:
1、
2、
3、
4、
例题8
计算:
疯狂操练8
计算下面各题:
1、……
2、
3、9.6+99.6+999.6+9999.6+99999.6
知识点九 转化为单位“1”
专题简析:
解答较复杂的分数应用题时,我们往往从题目中找出不变的量,把不变的量看作单位“1”,将已知条件进行转化,找出所求数量相当于单位“1”的几分之几,再列式解答。
.
例题1
有两筐梨。乙筐是甲筐的,从甲筐取出5千克梨放入乙筐后,乙筐的梨是甲筐的。
甲、乙两筐梨共重多少千克?
.
疯狂操练1
1、某小学低年级原有少先队员是非少先队员的,后来又有39名同学加入少先队组织。这样,少先队员的人数是非少先队员的。低年级有学生多少人?答 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
2、王师傅生产一批零件,不合格产品是合格产品的,后来从合格产品中又发现2个不合格产品,这时算出产品的合格率是94%。合格产品共有多少个?答 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
例题2
某学校原有长跳绳的根数占长、短跳绳总数的。后来又买进20根长跳绳,这时长跳绳的根数占长、短跳绳总数的。这个学校现有长、短跳绳的总数是多少根?
.
疯狂操练2
1、阅览室看书的同学中,女同学占,从阅览室走出5位女同学后,看书的同学中,女同学占,原来阅览室一共有多少名同学在看书?答 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
2、一堆什锦糖,其中奶糖占45%,再放入16千克其他糖后,奶糖只占25%,这堆糖中有奶糖多少千克?答 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
.
例题3
有两段布,一段布长40米,另一段布长30米,把两段布都用去同样长的一部分后,发现
短的一段布剩下的长度是长的一段布所剩长度的,每段布用去多少米?
疯狂操练3
1、有两根塑料绳,一根长80米,另一根长40米,如果从两根绳上各剪去同样长的一段后,短绳剩下的长度是长绳剩下的,两根绳各剪去多少米?答 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
2、今年父亲40岁,儿子12岁,当儿子的年龄是父亲的时,儿子多少岁?答 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
.
例题4
某商店原有黑白、彩色电视机共630台,其中黑白电视机占,后来又运进一些黑白电视机。这时黑白电视机占两种电视机总台数的30%,问:又运进黑白电视机多少台?
.
疯狂操练4
1、书店运来科技书和文艺书共240包,科技书占。后来又运来一批科技书,这时科技书占两种书总和的,现在两种书各有多少包?答 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
2、某市派出60名选手参加田径比赛,其中女选手占,正式比赛时,有几名女选手因故缺席,这样女选手人数占参赛选手总数的。问:正式参赛的女选手有多少人?
例题5
甲数是乙数、丙数、丁数之和的,乙数是甲数、丙数、丁数之和的,丙数是甲数、乙数、丁数之和的。已知丁数是260,求甲、乙、丙、丁四数之和。
疯狂操练5
1、甲、乙、丙、丁四个筑路队共筑1200米长的一段公路,甲队筑的路是其它三个队的,乙队筑的路是其它三个队的,丙队筑的路是其它三个队的,丁队筑路多少米?
甲、乙、丙三人共同购买一艘游艇,甲支付的钱是其余两人的,乙支付的钱是其余两人的,丙支付的钱恰好是5000元。这艘游艇的单价是多少元?
知识点十 牛吃草问题
专题简析:
牛吃草问题是牛顿问题,因牛顿提出而得名的。“一堆草可供10头牛吃3天,供6头牛吃几天?”这题很简单,用3×10÷6=5(天),如果把“一堆草”换成“一片正在生长的草地”,问题就不那么简单了。因为草每天走在生长,草的数量在不断变化。这类工作总量不固定(均匀变化)的问题就是“牛吃草”问题。
解答这类题的关键是要想办法从变化中找到不变的量。牧场上原有的草是不变的,新长出的草虽然在变化,因为是匀速生长,所以每天新长出的草是不变的。正确计算草地上原有的草及每天长出的草,问题就容易解决了。
例题1
一片青草地,每天都匀速长出青草,这片青草可供27头牛吃6周或23头牛吃9周。那么这片草地可供21头牛吃几周?
疯狂操练1
1、一片草地,每天都匀速长出青草,如果可供24头牛吃6天,20头牛吃10天吃完。那么可供19头牛吃几天?
2、牧场上一片草地,每天牧草都匀速生长。这片牧草可供10头牛吃20天,或者可供15头牛吃10天。问可供25头牛吃几天?
例题2
由于天气逐渐冷起来,牧场上的草不仅不长大,反而以固定的速度在减少。已知某块草地上的草可供20头牛吃5天或可供15头牛吃6天。照此计算,可供多少头牛吃10天?
疯狂操练2
1、由于天气逐渐变冷,牧场上的草每天以均匀的速度在减少。经计算,牧场上的草可供20头牛吃5天,或可供16头牛吃6天。那么可供11头牛吃几天?
2、经测算,地球上的资源可供100亿人生活100年,或可供80亿人生活300年。假设地球新生成的资源增长速度是一样的,那么,为满足人类不断发展的需要,地球最多能养活多少亿人?
例题3
自动扶梯以均匀速度由下往上行驶着,两位性急的孩子要从扶梯上楼。已知男孩每分钟走20级台阶,女孩每分钟15级台阶,结果男孩用5分钟到达楼上,女孩用了6分钟到达楼上。问:该扶梯共有多少级台阶?
疯狂操练3
1、自动扶梯以均匀速度行驶着,小明和小红要从扶梯上楼。已知小明每分钟走了25级台阶,小红每分钟走20级台阶,结果小明用5分钟、小红用了6分钟分别到达楼上。该扶梯共多少级台阶?
2、两个顽皮的孩子逆着自动扶梯的方向行走。在20秒钟里,男孩可走27级台阶,女孩可走24级台阶,男孩走了2分钟到达另一端,女孩走了3分钟到达另一端,该扶梯共多少级台阶?
例题4
一只船有一个漏洞,水以均匀的速度进入船内,发现漏洞时已经进了一些水。如果用12人舀水,3小时舀完。如果只有5个人舀水,要10小时才能舀完。现在要想2小时舀完,需要多少人?
疯狂操练4
1、有一水池,池底有泉水不断涌出。用10部抽水机20小时可以把水抽干,用15部相同的抽水机10小时可以把水抽干。那么用25部这样的抽水机多少小时可以把水抽干?
2、有一个长方形的水箱,上面有一个注水孔,底面有个出水孔,两孔同时打开后,如果每小时注水30立方分米,7小时可以注满水箱;如果每小时注水45立方分米,注满水箱可少用2.5小时。那么每小时由底面小孔排出多少立方分米的水(设每小时排水量相同)?
例题5
有三块草地,面积分别为5,6和8公顷。草地上的草一样厚,而且长得一样快。第一块草地可供11头牛吃10天,第二块草地可供12头牛吃14天。问第三块草地可供19头牛吃多少天?
疯狂操练5
1、某车站在检票前若干分钟就开始排队,每分钟来的旅客人数一样多。从开始检票到等候检票的队伍消失,同时开4个检票口需30分钟,同时开5个检票口需20分钟。如果同时打开7个检票口,那么需要多少分钟?
2、快、中、慢三车同时从A地出发,追赶一辆正在行驶的自行车,三车的速度分别是每小时24千米、20千米、19千米。快车追上自行车用了6小时,中车追上自行车用了10小时,慢车追上自行车用多少小时?
知识点一 四则运算的意义
整数加法、小数加法、分数加法的意义:把两个数合成一个数的运算
整数减法、小数减法、分数减法的意义:已知两个数的和与其中的一个加数,求另一个加数的运算
整数乘法的意义:求几个相同加数的和的简便运算
小数乘法的意义:小数乘整数与整数乘法的意义相同;一个数乘小数,就是求这个数的十分之几、百分之几……是多少。
整数乘分数的意义:一个数乘分数,就是求这个数的几分之几是多少
分数乘整数的意义:分数乘整数,就是求几个相同分数的和的简便运算
整数除法、小数除法、分数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。
知识点二 四则运算的计算方法
1、加减法的计算方法
(1)整数的加法:相同数位对齐,从低位加起,哪一位上的数相加满十,就要向前一位进一。
(2)整数的减法:相同数位对齐,从低位减起,哪一位上的数不够减要从前一位上退一,在本位上加上10再减。
(3)小数的加减法:计算小数加减法时,先把小数点对齐(也就是相同的数位对齐),再按照整数加减法的法则进行计算,最后在得数里对齐横线上的小数点,点上小数点
(4)分数的加减法:同分母的分数相加减,分母不变,只把分子相加减;异分母的分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
2、乘法的计算方法
(1)整数的乘法:从低位到高位分别用因数的每一位去乘另一个因数;用一个因数的哪一位去乘,求得的数的末位就要和那一位对齐;然后把几次求得的积加起来
(2)小数乘法:先按照整数乘法的法则算出积,再看因数中一共有几位小数,就从积的右边起数出几位点上小数点
(3)分数乘法:分数乘整数,用分数的分子和整数相乘的积作分子,分母不变;分数乘分数,用分子相乘的积作分子,分母相乘的积作分母。
3、除法的计算方法
(1)整数的除法:从被除数的高位除起,除数有几位就先看被除数的前几位,如果前几位比除数小,就多取一位再除,除到哪一位,商就写在那一位的上面;每次除得的余数必须比除数小;在求出商的最高位以后,如果被除数的哪一位上不够商1,就在那一位上写0
(2)小数除法:除数是整数时,按照整数除法进行计算,商的小数点要与被除数的小数点对齐。除数是小数时,要先把除数转化成整数,同时把被除数扩大相同的倍数,然后按照除数是整数的除法进行计算。
(3)分数的除法:甲数除以乙数(0除外),等于甲数乘乙数的倒数。
知识点三 整数四则运算中各部分间的关系
1、加法:和=加数+加数 加数=和-另一个加数
2、减法:差=被减数-减数 减数=被减数-差 被减数=减数+差
3、乘法:积=因数×因数 一个因数=积÷另一个因数
4、除法:商=被除数÷除数 除数=被除数÷商 被除数=除数×商
知识点四 四则运算的估算方法
根据算式中各数的特点,估算时一般是将其中的大数看作整十、整百、整千……的数,使原式通过口算便可求出得数。由于得数是近似值,所以计算时要用≈连接
知识点五 四则运算定律、运算性质
1、运算定律
(1)加法结合律:两个数相加,交换加数的位置,它们的和不变 a+b=b+a
(2)加法结合律:三个数相加,先把前两个数相加,再加上第三个数,或者先把后面两个数相加,再和第一个相加,它们的和不变。a+b+c=(a+b)+c=a+(b+c)
(3)乘法交换律: 两个数相乘,交换因数的位置,它们的积不变。a×b=b×a
(4)乘法结合律:三个数相乘,先把前两个数相乘,再乘第三个数,或者先把后面两个数相乘,再和第一个数相乘,它们的积不变。a×b×c=(a×b) ×c=a×(b×c)
(5)乘法分配律:两个数的和与一个数相乘,等于把这两个数分别与这个数相乘,再把两个积加起来。(a+b) ×c=a×c+b×c a×(b+c)=a×b+a×c
2、运算性质
(1)减法的运算性质:a-(b+c)=a-b-c a-(b-c)=a-b+c
(2)除法的运算性质(除数不为0):
a÷(b×c)=a÷b÷c a÷(b÷c)=a÷b×c
(a+b)÷c=a÷c+b÷c (a-b) ÷c=a÷c-b÷c
知识点六 四则混合运算的顺序
四则运算分为两级:加法和减法叫做第一级运算;乘法和除法叫做第二级运算。
(1)在没有括号的算式里,如果只含有同一级运算,要从左往右依次计算;如果含有两级运算,要先做第二级运算,再做第一级运算。
(2)在有括号的算式里,要先算小括号里面的,再算中括号里面的,最后算括号外面的。
疯狂操练一
(8+3)-( - ) 13.76-(+1.76+1)
(×)×(13×18) 19.98×37-199.8×1.9+1998×0.82
35.2÷9+35.2÷ 0.25×1.25×320
6×+13÷4-18×0.25 0.32×6.7+3.2×0.43-0.32
7.6×÷【1.9-1.9×(1.9-1.9)】 2.5×12.5×32-37-563
1×1×1×1×1 9-15÷19-×2
3.26×【1÷(-)】 (+)+(-)-(+)
(2.5+2.5+2.5+2.5) ×25×8 (+++)×(1-)
(6.9×0.125×1.75) ÷(2.3××) 【(-÷2) ×+1÷6】÷0.01
0.61×0.25+0.18×+0.21×25% (3+÷+3) -(7×÷7×)
【5-(0.5×9+×)】÷ (12+) ×2.5+(9+10)× 2
1×【7+(4.125-)-4】 5-【1-(2.5-1)】÷0.125
1000÷32÷0.25÷1.25
知识点七 简便运算一
专题简析:
根据算式的结构和数的特征,灵活运用运算法则、定律、性质和某些公式,可以把一些较复杂的四则混合运算化繁为简,化难为易。
例题1
计算:4.75-9.63+(8.25-1.37)
疯狂操练1
计算下面各题:
1、6.73-2+(3.27-1) 2、
3、14.15-()-2.125 4、
例题2
计算:36×1.09+1.2×67.3
疯狂操练2
计算:
1、45×2.08+1.5×37.6 2、52×11.1+2.6×778
3、48×1.08+1.2×56.8 4、72×2.09-1.8×73.6
例题3
计算:333387
疯狂操练3
计算下面各题:
1、 2、
3、 4、
例题4
计算:
疯狂操练4
计算下面各题:
1、 2、
3、
例题5
计算:81.5×15.8+81.5×51.8+67.6×18.5
疯狂操练5
1、53.5×35.3+53.5×43.2+78.5×46.5
2、235×12.1+235×42.2-135×54.3
3、3.75×735-×5730+16.2×62.5
例题6
计算:
疯狂操练6
计算下面各题:
1、99999×77778+33333×66666 2、34.5×76.5-345×6.42-123×1.45
3、77×13+255×999+510
知识点八 简便运算二
专题简析:
在进行分数运算时,除了牢记运算定律、性质外,还要仔细审题,仔细观察运算符号和数字特点,合理地把参加运算的数拆开或者合并进行重新组合,使其变成符合运算定律的模式,以便于口算,从而简化运算。
在后面的四个例题中,将着重向同学们介绍怎样用拆分法(也叫裂项法、拆项法)进行分数的简便运算。运用拆分法解题主要是使拆开后的一些分数互相抵消,达到简化运算的目的。一般地,形如的分数可以拆成;形如的分数可以拆成;形如的分数可以拆成等等。同学们可以结合例题思考其中的规律。
例题1
计算:(1) (2)
疯狂操练1
用简便方法计算下面各题:
1、×8 2、×126 3、35×
4、73× 5、×1999
例题2
计算:73×
疯狂操练2
计算下面各题:
1、64× 2、22×
3、×57 4、41×+51×
例题3
计算:
疯狂操练3
计算下面各题:
1、×39+×27 2、×35+×17
3、×5+×5+×10
例题4
计算:
疯狂操练4
计算下面各题:
1、 2、
3、 4、
例题5
计算:
疯狂操练5
计算下面各题:
1、
2、
3、
4、
例题6
计算
疯狂操练6
计算下面各题:
1、
2、+++……+
3、
4、++++
例题7
计算:
疯狂操练7
计算下面各题:
1、
2、
3、
4、
例题8
计算:
疯狂操练8
计算下面各题:
1、……
2、
3、9.6+99.6+999.6+9999.6+99999.6
知识点九 转化为单位“1”
专题简析:
解答较复杂的分数应用题时,我们往往从题目中找出不变的量,把不变的量看作单位“1”,将已知条件进行转化,找出所求数量相当于单位“1”的几分之几,再列式解答。
.
例题1
有两筐梨。乙筐是甲筐的,从甲筐取出5千克梨放入乙筐后,乙筐的梨是甲筐的。
甲、乙两筐梨共重多少千克?
.
疯狂操练1
1、某小学低年级原有少先队员是非少先队员的,后来又有39名同学加入少先队组织。这样,少先队员的人数是非少先队员的。低年级有学生多少人?答 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
2、王师傅生产一批零件,不合格产品是合格产品的,后来从合格产品中又发现2个不合格产品,这时算出产品的合格率是94%。合格产品共有多少个?答 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
例题2
某学校原有长跳绳的根数占长、短跳绳总数的。后来又买进20根长跳绳,这时长跳绳的根数占长、短跳绳总数的。这个学校现有长、短跳绳的总数是多少根?
.
疯狂操练2
1、阅览室看书的同学中,女同学占,从阅览室走出5位女同学后,看书的同学中,女同学占,原来阅览室一共有多少名同学在看书?答 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
2、一堆什锦糖,其中奶糖占45%,再放入16千克其他糖后,奶糖只占25%,这堆糖中有奶糖多少千克?答 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
.
例题3
有两段布,一段布长40米,另一段布长30米,把两段布都用去同样长的一部分后,发现
短的一段布剩下的长度是长的一段布所剩长度的,每段布用去多少米?
疯狂操练3
1、有两根塑料绳,一根长80米,另一根长40米,如果从两根绳上各剪去同样长的一段后,短绳剩下的长度是长绳剩下的,两根绳各剪去多少米?答 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
2、今年父亲40岁,儿子12岁,当儿子的年龄是父亲的时,儿子多少岁?答 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
.
例题4
某商店原有黑白、彩色电视机共630台,其中黑白电视机占,后来又运进一些黑白电视机。这时黑白电视机占两种电视机总台数的30%,问:又运进黑白电视机多少台?
.
疯狂操练4
1、书店运来科技书和文艺书共240包,科技书占。后来又运来一批科技书,这时科技书占两种书总和的,现在两种书各有多少包?答 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
2、某市派出60名选手参加田径比赛,其中女选手占,正式比赛时,有几名女选手因故缺席,这样女选手人数占参赛选手总数的。问:正式参赛的女选手有多少人?
例题5
甲数是乙数、丙数、丁数之和的,乙数是甲数、丙数、丁数之和的,丙数是甲数、乙数、丁数之和的。已知丁数是260,求甲、乙、丙、丁四数之和。
疯狂操练5
1、甲、乙、丙、丁四个筑路队共筑1200米长的一段公路,甲队筑的路是其它三个队的,乙队筑的路是其它三个队的,丙队筑的路是其它三个队的,丁队筑路多少米?
甲、乙、丙三人共同购买一艘游艇,甲支付的钱是其余两人的,乙支付的钱是其余两人的,丙支付的钱恰好是5000元。这艘游艇的单价是多少元?
知识点十 牛吃草问题
专题简析:
牛吃草问题是牛顿问题,因牛顿提出而得名的。“一堆草可供10头牛吃3天,供6头牛吃几天?”这题很简单,用3×10÷6=5(天),如果把“一堆草”换成“一片正在生长的草地”,问题就不那么简单了。因为草每天走在生长,草的数量在不断变化。这类工作总量不固定(均匀变化)的问题就是“牛吃草”问题。
解答这类题的关键是要想办法从变化中找到不变的量。牧场上原有的草是不变的,新长出的草虽然在变化,因为是匀速生长,所以每天新长出的草是不变的。正确计算草地上原有的草及每天长出的草,问题就容易解决了。
例题1
一片青草地,每天都匀速长出青草,这片青草可供27头牛吃6周或23头牛吃9周。那么这片草地可供21头牛吃几周?
疯狂操练1
1、一片草地,每天都匀速长出青草,如果可供24头牛吃6天,20头牛吃10天吃完。那么可供19头牛吃几天?
2、牧场上一片草地,每天牧草都匀速生长。这片牧草可供10头牛吃20天,或者可供15头牛吃10天。问可供25头牛吃几天?
例题2
由于天气逐渐冷起来,牧场上的草不仅不长大,反而以固定的速度在减少。已知某块草地上的草可供20头牛吃5天或可供15头牛吃6天。照此计算,可供多少头牛吃10天?
疯狂操练2
1、由于天气逐渐变冷,牧场上的草每天以均匀的速度在减少。经计算,牧场上的草可供20头牛吃5天,或可供16头牛吃6天。那么可供11头牛吃几天?
2、经测算,地球上的资源可供100亿人生活100年,或可供80亿人生活300年。假设地球新生成的资源增长速度是一样的,那么,为满足人类不断发展的需要,地球最多能养活多少亿人?
例题3
自动扶梯以均匀速度由下往上行驶着,两位性急的孩子要从扶梯上楼。已知男孩每分钟走20级台阶,女孩每分钟15级台阶,结果男孩用5分钟到达楼上,女孩用了6分钟到达楼上。问:该扶梯共有多少级台阶?
疯狂操练3
1、自动扶梯以均匀速度行驶着,小明和小红要从扶梯上楼。已知小明每分钟走了25级台阶,小红每分钟走20级台阶,结果小明用5分钟、小红用了6分钟分别到达楼上。该扶梯共多少级台阶?
2、两个顽皮的孩子逆着自动扶梯的方向行走。在20秒钟里,男孩可走27级台阶,女孩可走24级台阶,男孩走了2分钟到达另一端,女孩走了3分钟到达另一端,该扶梯共多少级台阶?
例题4
一只船有一个漏洞,水以均匀的速度进入船内,发现漏洞时已经进了一些水。如果用12人舀水,3小时舀完。如果只有5个人舀水,要10小时才能舀完。现在要想2小时舀完,需要多少人?
疯狂操练4
1、有一水池,池底有泉水不断涌出。用10部抽水机20小时可以把水抽干,用15部相同的抽水机10小时可以把水抽干。那么用25部这样的抽水机多少小时可以把水抽干?
2、有一个长方形的水箱,上面有一个注水孔,底面有个出水孔,两孔同时打开后,如果每小时注水30立方分米,7小时可以注满水箱;如果每小时注水45立方分米,注满水箱可少用2.5小时。那么每小时由底面小孔排出多少立方分米的水(设每小时排水量相同)?
例题5
有三块草地,面积分别为5,6和8公顷。草地上的草一样厚,而且长得一样快。第一块草地可供11头牛吃10天,第二块草地可供12头牛吃14天。问第三块草地可供19头牛吃多少天?
疯狂操练5
1、某车站在检票前若干分钟就开始排队,每分钟来的旅客人数一样多。从开始检票到等候检票的队伍消失,同时开4个检票口需30分钟,同时开5个检票口需20分钟。如果同时打开7个检票口,那么需要多少分钟?
2、快、中、慢三车同时从A地出发,追赶一辆正在行驶的自行车,三车的速度分别是每小时24千米、20千米、19千米。快车追上自行车用了6小时,中车追上自行车用了10小时,慢车追上自行车用多少小时?
同课章节目录
