人教版数学八年级下册 19.1.2 函数的图像 课件(共21张PPT)
文档属性
| 名称 | 人教版数学八年级下册 19.1.2 函数的图像 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 895.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 21:07:45 | ||
图片预览






文档简介
(共21张PPT)
函数的图像
“产油之王” —广299-1
创设情景
新知导入
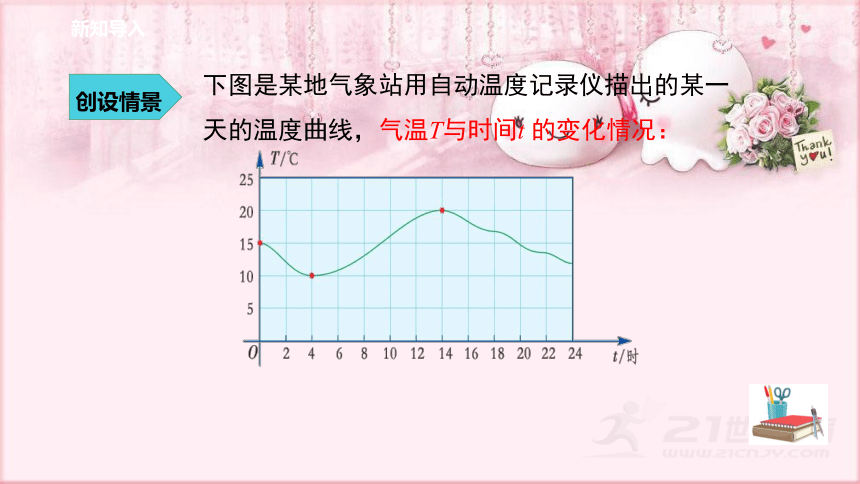
下图是某地气象站用自动温度记录仪描出的某一天的温度曲线,气温T与时间t 的变化情况:
练一练
问题1:表示函数有哪三种方法?
列表法、解析式法和图象法.
问题2:这三种表示的方法各有什么优点?
1.列表法比较直观、准确地表示出函数中两个变量之间的关系;
2.解析式法比较准确、全面地表示出函数中两个变量之间的关系;
3.图象法比较形象、直观地表示出函数中两个变量之间的关系.
注意:在遇到实际问题时,就要要根据具体情况选择适当的方法,有时为全面地认识问题,需要几种方法同时使用,即具体问题具体分析。
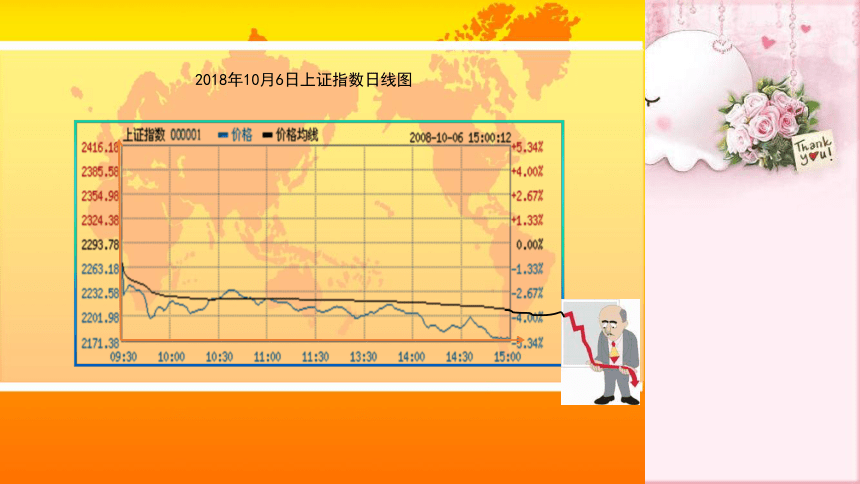
2018年10月6日上证指数日线图
想一想
新知讲解
问题2 怎样获得组成图形的点?
先确定点的坐标.
取一些自变量的值,计算出相应的函数值.
问题3 怎样确定满足函数关系的点的坐标?
问题1 在平面直角坐标系中,平面内的点与有序数对有怎样的关系?
点与有序数对一一对应
练一练
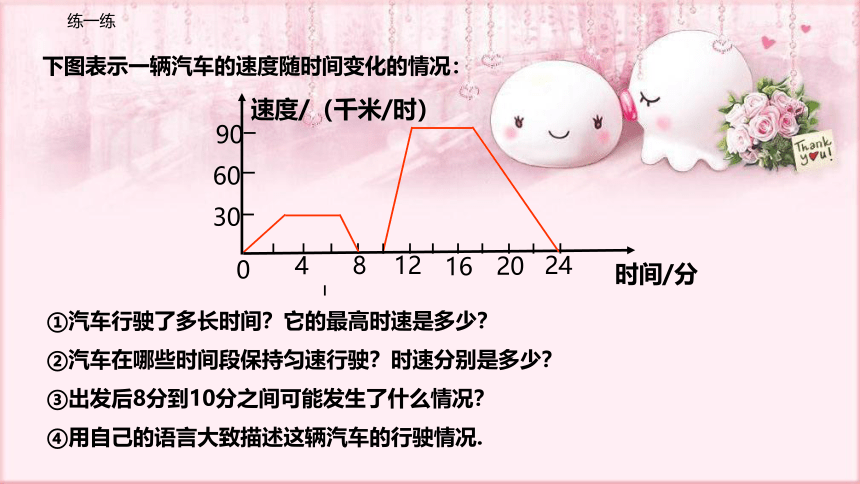
下图表示一辆汽车的速度随时间变化的情况:
①汽车行驶了多长时间?它的最高时速是多少?
②汽车在哪些时间段保持匀速行驶?时速分别是多少?
③出发后8分到10分之间可能发生了什么情况?
④用自己的语言大致描述这辆汽车的行驶情况.
0
4
8
20
12
16
时间/分
24
30
60
90
速度/(千米/时)
如何画函数 的图象?
分析:
在直角坐标系中描点
1.函数图象是由点组成的图形.
2.把自变量与函数的每对对应值分别作为点的横纵坐标.
函数的自变量x的值为横坐标相应的函数值y的值为纵坐标
列出一些由函数的自变量及其对应值组成的有序实数对
形成概念
新知讲解
O
S
x
1
2
3
4
1
4
9
16
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
函数S=x2 (x>0)的图象.
练一练
一水库的水位在最近5 h内持续上涨,下表记录了这5 h内6个时间点的水位高度,其中t表示时间,y表示水温高度.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
问题一 在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律吗?
是,水位越来越高
1、作函数 的图象.
解:
所得图象即为所求.
y
2
1
-1
-2
x
-1
-0.5
0
0
0.5
1
…
…
…
…
练习
典型例题
新知讲解
例1 如图1,小明家、食堂、图书馆在同一条直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.图2反映了这个过程中,小明离家的距离y与时间x之间的对应关系.
图 1
图 2
从图像中获取信息解题
甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(米)与时间(秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
A.乙队率先到达终点
B.甲队比乙队多走了米
C.在秒时,两队所走路程相等
D.从出发到秒的时间段内,乙队的速度慢
【答案】C
【详解】
解:、由函数图象可知,甲走完全程需要秒,乙走完全程需要秒,甲队率先到达终点,本选项错误;
、由函数图象可知,甲、乙两队都走了米,路程相同,本选项错误;
、由函数图象可知,在秒时,两队所走路程相等,均为米,本选项正确;
、由函数图象可知,从出发到秒的时间段内,甲队的速度慢,本选项错误;
故选.
2、作函数 (x>0)图象
解:
练习
y
…
5
4
3
2
1
x
-6
-3
-2
-1.5
-1.2
…
…
…
解析式法
列表法
图象法
(x>0)
6
5
4
3
2
1
0
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
从图像中获取信息解题
已知动点P以每秒2 cm的速度沿图(1)的边框按从B C D E F A的路径移动,相应的△ABP的面积S与时间t之间的关系如图(2)中的图象表示.若AB=6 cm,试回答下列问题:
(1)图(1)中的BC长是多少 (2)图(2)中的a是多少
(3)图(1)中的图形面积是多少 (4)图(2)中的b是多少
【分析】(1)根据题意得:动点P在BC上运动的时间是4秒,又由动点的速度,可得BC的长;
(2)由(1)可得BC的长,又由AB=6cm,可以计算出△ABP的面积,计算可得a的值;
(3)分析图形可得,甲中的图形面积等于AB×AF-CD×DE,根据图象求出CD和DE的长,代入数据计算可得答案,
(4)计算BC+CD+DE+EF+FA的长度,又由P的速度,计算可得b的值.
【详解】(1)由图象知,当t由0增大到4时,点P由B C,∴BC==4×2=8(㎝) ;
(2) a=S△ABC=×6×8=24(㎝2) ;
(3) 同理,由图象知 CD=4㎝,DE=6㎝,则EF=2㎝,AF=14㎝
∴图1中的图象面积为6×14-4×6=60㎝2 ;
(4) 图1中的多边形的周长为(14+6)×2=40㎝ b=(40-6)÷2=17秒.
典型例题
新知讲解
例1 如图1,小明家、食堂、图书馆在同一条直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.图2反映了这个过程中,小明离家的距离y与时间x之间的对应关系.
根据图象回答下列问题:
(4)小明读报用了多长时间?
58-28=30,小明读报用了30min.
(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
图书馆离小明家0.8km,小明从图书馆回家用了68-58=10(min),由此算出的平均速度是0.08km/min.
b
c
d
e
a
y/千米
x/分钟
问题1:小新从家走到书店用了多少时间?
小新从家里出发去书店看书,又去运动场打球,然后回家,其中x表示时间,y表示小新离他家的距离.(注:小新的家,书店,运动场依次在同一直线上)
从横坐标看出我去书店用了15分钟.
小新妈妈的困惑
实践
(2) (x>0)
从函数图象可以看出,曲线从左向右下降,即当x由小变大时,
随之减小.
(x>0)
x … 0.5 1 1.5 2 2.5 3 3.5 4 5 6 …
y … 6 3 2 1.5 …
12
4
2.4
1.2
1
y
6
2
1
3
4
5
1
2
3
4
5
6
(x>0)
列表:
描点:
连线:
典型例题
新知讲解
在一次实验中,小明把一根弹簧的上端固定、在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体质量x的一组对应值.
①上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
②当所挂物体重量为3千克时,弹簧多长?不挂重物时呢?
③若所挂重物为7千克时(在允许范围内),你能说出此时的弹簧长度吗?
函数的三种表示方法
【解析】
(1)上表反映了弹簧长度与所挂物体质量之间的关系;
其中所挂物体质量是自变量;
(2)当所挂物体重量为3千克时,弹簧长24厘米;
当不挂重物时,弹簧长18厘米;
(3)根据上表可知所挂重物为7千克时(在允许范围内)时的弹簧长度=18+2×7=32(厘米).
1、认识了什么是函数的图象
2、学会了如何去画函数的图象
3、探索了函数图象的实际应用
快乐总结
请谈谈你的收获!与大家分享.
聪明出于勤奋,天才在于积累。
函数的图像
“产油之王” —广299-1
创设情景
新知导入
下图是某地气象站用自动温度记录仪描出的某一天的温度曲线,气温T与时间t 的变化情况:
练一练
问题1:表示函数有哪三种方法?
列表法、解析式法和图象法.
问题2:这三种表示的方法各有什么优点?
1.列表法比较直观、准确地表示出函数中两个变量之间的关系;
2.解析式法比较准确、全面地表示出函数中两个变量之间的关系;
3.图象法比较形象、直观地表示出函数中两个变量之间的关系.
注意:在遇到实际问题时,就要要根据具体情况选择适当的方法,有时为全面地认识问题,需要几种方法同时使用,即具体问题具体分析。
2018年10月6日上证指数日线图
想一想
新知讲解
问题2 怎样获得组成图形的点?
先确定点的坐标.
取一些自变量的值,计算出相应的函数值.
问题3 怎样确定满足函数关系的点的坐标?
问题1 在平面直角坐标系中,平面内的点与有序数对有怎样的关系?
点与有序数对一一对应
练一练
下图表示一辆汽车的速度随时间变化的情况:
①汽车行驶了多长时间?它的最高时速是多少?
②汽车在哪些时间段保持匀速行驶?时速分别是多少?
③出发后8分到10分之间可能发生了什么情况?
④用自己的语言大致描述这辆汽车的行驶情况.
0
4
8
20
12
16
时间/分
24
30
60
90
速度/(千米/时)
如何画函数 的图象?
分析:
在直角坐标系中描点
1.函数图象是由点组成的图形.
2.把自变量与函数的每对对应值分别作为点的横纵坐标.
函数的自变量x的值为横坐标相应的函数值y的值为纵坐标
列出一些由函数的自变量及其对应值组成的有序实数对
形成概念
新知讲解
O
S
x
1
2
3
4
1
4
9
16
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
函数S=x2 (x>0)的图象.
练一练
一水库的水位在最近5 h内持续上涨,下表记录了这5 h内6个时间点的水位高度,其中t表示时间,y表示水温高度.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
问题一 在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律吗?
是,水位越来越高
1、作函数 的图象.
解:
所得图象即为所求.
y
2
1
-1
-2
x
-1
-0.5
0
0
0.5
1
…
…
…
…
练习
典型例题
新知讲解
例1 如图1,小明家、食堂、图书馆在同一条直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.图2反映了这个过程中,小明离家的距离y与时间x之间的对应关系.
图 1
图 2
从图像中获取信息解题
甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(米)与时间(秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
A.乙队率先到达终点
B.甲队比乙队多走了米
C.在秒时,两队所走路程相等
D.从出发到秒的时间段内,乙队的速度慢
【答案】C
【详解】
解:、由函数图象可知,甲走完全程需要秒,乙走完全程需要秒,甲队率先到达终点,本选项错误;
、由函数图象可知,甲、乙两队都走了米,路程相同,本选项错误;
、由函数图象可知,在秒时,两队所走路程相等,均为米,本选项正确;
、由函数图象可知,从出发到秒的时间段内,甲队的速度慢,本选项错误;
故选.
2、作函数 (x>0)图象
解:
练习
y
…
5
4
3
2
1
x
-6
-3
-2
-1.5
-1.2
…
…
…
解析式法
列表法
图象法
(x>0)
6
5
4
3
2
1
0
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
从图像中获取信息解题
已知动点P以每秒2 cm的速度沿图(1)的边框按从B C D E F A的路径移动,相应的△ABP的面积S与时间t之间的关系如图(2)中的图象表示.若AB=6 cm,试回答下列问题:
(1)图(1)中的BC长是多少 (2)图(2)中的a是多少
(3)图(1)中的图形面积是多少 (4)图(2)中的b是多少
【分析】(1)根据题意得:动点P在BC上运动的时间是4秒,又由动点的速度,可得BC的长;
(2)由(1)可得BC的长,又由AB=6cm,可以计算出△ABP的面积,计算可得a的值;
(3)分析图形可得,甲中的图形面积等于AB×AF-CD×DE,根据图象求出CD和DE的长,代入数据计算可得答案,
(4)计算BC+CD+DE+EF+FA的长度,又由P的速度,计算可得b的值.
【详解】(1)由图象知,当t由0增大到4时,点P由B C,∴BC==4×2=8(㎝) ;
(2) a=S△ABC=×6×8=24(㎝2) ;
(3) 同理,由图象知 CD=4㎝,DE=6㎝,则EF=2㎝,AF=14㎝
∴图1中的图象面积为6×14-4×6=60㎝2 ;
(4) 图1中的多边形的周长为(14+6)×2=40㎝ b=(40-6)÷2=17秒.
典型例题
新知讲解
例1 如图1,小明家、食堂、图书馆在同一条直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.图2反映了这个过程中,小明离家的距离y与时间x之间的对应关系.
根据图象回答下列问题:
(4)小明读报用了多长时间?
58-28=30,小明读报用了30min.
(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
图书馆离小明家0.8km,小明从图书馆回家用了68-58=10(min),由此算出的平均速度是0.08km/min.
b
c
d
e
a
y/千米
x/分钟
问题1:小新从家走到书店用了多少时间?
小新从家里出发去书店看书,又去运动场打球,然后回家,其中x表示时间,y表示小新离他家的距离.(注:小新的家,书店,运动场依次在同一直线上)
从横坐标看出我去书店用了15分钟.
小新妈妈的困惑
实践
(2) (x>0)
从函数图象可以看出,曲线从左向右下降,即当x由小变大时,
随之减小.
(x>0)
x … 0.5 1 1.5 2 2.5 3 3.5 4 5 6 …
y … 6 3 2 1.5 …
12
4
2.4
1.2
1
y
6
2
1
3
4
5
1
2
3
4
5
6
(x>0)
列表:
描点:
连线:
典型例题
新知讲解
在一次实验中,小明把一根弹簧的上端固定、在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体质量x的一组对应值.
①上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
②当所挂物体重量为3千克时,弹簧多长?不挂重物时呢?
③若所挂重物为7千克时(在允许范围内),你能说出此时的弹簧长度吗?
函数的三种表示方法
【解析】
(1)上表反映了弹簧长度与所挂物体质量之间的关系;
其中所挂物体质量是自变量;
(2)当所挂物体重量为3千克时,弹簧长24厘米;
当不挂重物时,弹簧长18厘米;
(3)根据上表可知所挂重物为7千克时(在允许范围内)时的弹簧长度=18+2×7=32(厘米).
1、认识了什么是函数的图象
2、学会了如何去画函数的图象
3、探索了函数图象的实际应用
快乐总结
请谈谈你的收获!与大家分享.
聪明出于勤奋,天才在于积累。
