人教版数学八年级下册 19.2.1 正比列函数 课件(共21张PPT)
文档属性
| 名称 | 人教版数学八年级下册 19.2.1 正比列函数 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 389.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 21:17:49 | ||
图片预览








文档简介
(共21张PPT)
正比列函数
正比例函数的概念
温故
一般地,在一个变化过程中,如果有两个变量
x和y,并且对于x的每一个确定的值,y都有
唯一确定的值与其对应,那么我们就说x是
自变量,y是x的函数.
函数的概念
表示自变量与函数之间的关系的数学式子,叫做函数的解析式。
情景引入
2011年开始运营的京沪高速铁路全长1318km.设列车平均速度为300km/h。考虑以下问题:
3)京沪高铁列车从北京南站出发2.5h后,是否已经过了距
始发站1100km的南京站?
从北京南站出发2.5h的行程,即当t=2.5h时y的值
y=300t=2.5*300=750km
因为750km<1100km
所以这事列车尚未到达距始发站1100km的南京站。
一般地,形如 y=kx(k是常数,k≠0)的函数,叫做正比例函数, 其中k叫做比例系数.
注: 正比例函数解析式y=kx(k≠0)的结构特征:
①k≠0
②x的次数是1
自变量x的取值范围为一切实数
互助探究(感知概念)
引入新知
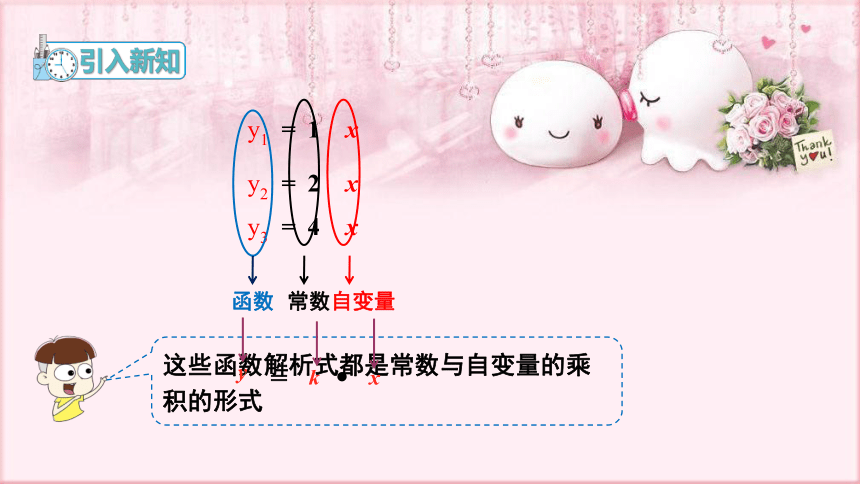
y1 = 1 x
y2 = 2 x
y3 = 4 x
自变量
这些函数解析式都是常数与自变量的乘积的形式
函数
常数
y
k
x
=
正比例函数
【问题】在正比例函数y=kx(k为常数,k≠0)中关键是确定哪个量?比例系数k一经确定,正比例函数确定了吗?怎样确定k呢?
从函数关系看,关键是比例系数k,比例系数k一确定,正比例函数就确了;只需知道两个变量x、y的一对对应值即可确定k值。
从方程角度看,如果三个量x、y、k中已知其中两个量,则一定可以求出第三个量。
一般地,形如 y=kx(k 是常数,k≠0)的函数,叫做正比例函数,其中k 叫做比例系数.
解:(1)因为y是x的正比例函数,所以设解析
式为y=kx(k≠0)
把 x =-4, y =2 代入上式,得
2 = -4k
解得
(2)当 x=6 时, y = -3.
已知y是x的正比例函数,且当x=-4时,y=2。
(1)求y与x之间的函数解析式。
(2)当x=6时,求函数y的值。
设
代
求
写
待定系数法
所以y与x之间的函数解析式为 y= - x
例
2
1
k= -
探究(二)
例2.列式表示下列问题中变量之间的函数关系,并判断是不是正比例函数.
(1)圆的周长l 随半径r的变化而变化.
典例分析
(2)冷冻一个0℃的物体,使它每分钟下降2℃,物体温度T(单位:℃)随冷冻时间t(单位:min)的变化而变化.
是正比例函数,比例系数为2π
T=-2t
是正比例函数,比例系数为-2
(r>0)
(t≥0)
课堂测试
下列说法正确的打“√”,错误的打“×”
(1)若y=kx,则y是x的正比例函数( )
(2)若y=3x2,则y是x的正比例函数( )
(3)若y=2(x-2)+4,则y是x的正比例函数( )
(4)若y=7(x-1) ,则y是x-1的正比例函数( )
这节课我学会(懂得)了……
总结归纳
正比例函数解析式y=kx(k≠0)的结构特征:
k是常数,k≠0
自变量x的次数是1
k与x是乘积关系 y=kx,称y与x成正比例,反之,
若y与x成正比例,可以设 y=kx
正比例函数解析式的一般式:
(k是常数,k≠0)
y = k · x
x的指数是1。
所以自变量 x 的次数为 1,即 a-2=1.
解得:a=3.
探索与思考
画出下列正比例函数的图像
1)y=2x,y=x
2)y=-1.5x,y=-4x
提示:列表—描点—连线
x -2 -1 0 1 2
y 3 1.5 0 -1.5 -3
2)函数y=-1.5x
函数y=-4x
x -2 -1 0 1 2
y 8 4 0 -4 -8
y=-1.5x
y=-4x
观察与思考
y=-1.5x
y=-4x
对一般正比例函数y =kx,当k < 0时,
(1)它的图象形状是什么?
(2)经过哪个象限?
(3)变化趋势怎样
(4)经过哪些特殊点
(5)哪个陡,哪个平缓
直线
二、四象限
y随x的增加而减小
经过原点(0,0)
k越大越缓
探究新知
(一)请画出下列函数的图像
x
1
2
3
4
-1
-2
-3
-4
y
1
2
3
4
-1
-2
-3
-4
1、图像是一条直线;
2、图像经过一、三象限;
3、图像从左往右依次上升;
4、y随x的增大而增大。
3. 点P(-1,3)在正比例函数y=kx的图像上,
则k的 值为_________.
K=-3
例题精讲
例1、已知正比例函数y=(1-2a)x
(1)若函数的图像经过原点和第一、三象限,则a的取值范围是多少?
理解正比例函数的性质
已知y=(k﹣3)是关于x的正比例函数,
(1)写出y与x之间的函数解析式:
(2)求当x=﹣4时,y的值.
【详解】
(1)当k2﹣8=1,且k﹣3≠0时,y是x的正比例函数,
故k=﹣3时,y是x的正比例函数,
∴y=﹣6x;
(2)当x=﹣4时,y=﹣6×(﹣4)=24.
理解正比例函数的概念
在 y=5x+2-a 中,若是 的正比例函数,则常数 _____.
【详解】解:因为是 的正比例函数,则a-2=0,a=2
小结
正比例函数
定义
注意
一般地,形如y=kx(k是常数, k≠0)的函数,叫做正比例函数, 其中 k 叫做比例系数.
①比例系数 k 是常数,且 k≠0;
②两个变量 x、y 的次数都是1.
待定系数法求解析式
一设
二列
三解
四写
聪明出于勤奋,天才在于积累。
正比列函数
正比例函数的概念
温故
一般地,在一个变化过程中,如果有两个变量
x和y,并且对于x的每一个确定的值,y都有
唯一确定的值与其对应,那么我们就说x是
自变量,y是x的函数.
函数的概念
表示自变量与函数之间的关系的数学式子,叫做函数的解析式。
情景引入
2011年开始运营的京沪高速铁路全长1318km.设列车平均速度为300km/h。考虑以下问题:
3)京沪高铁列车从北京南站出发2.5h后,是否已经过了距
始发站1100km的南京站?
从北京南站出发2.5h的行程,即当t=2.5h时y的值
y=300t=2.5*300=750km
因为750km<1100km
所以这事列车尚未到达距始发站1100km的南京站。
一般地,形如 y=kx(k是常数,k≠0)的函数,叫做正比例函数, 其中k叫做比例系数.
注: 正比例函数解析式y=kx(k≠0)的结构特征:
①k≠0
②x的次数是1
自变量x的取值范围为一切实数
互助探究(感知概念)
引入新知
y1 = 1 x
y2 = 2 x
y3 = 4 x
自变量
这些函数解析式都是常数与自变量的乘积的形式
函数
常数
y
k
x
=
正比例函数
【问题】在正比例函数y=kx(k为常数,k≠0)中关键是确定哪个量?比例系数k一经确定,正比例函数确定了吗?怎样确定k呢?
从函数关系看,关键是比例系数k,比例系数k一确定,正比例函数就确了;只需知道两个变量x、y的一对对应值即可确定k值。
从方程角度看,如果三个量x、y、k中已知其中两个量,则一定可以求出第三个量。
一般地,形如 y=kx(k 是常数,k≠0)的函数,叫做正比例函数,其中k 叫做比例系数.
解:(1)因为y是x的正比例函数,所以设解析
式为y=kx(k≠0)
把 x =-4, y =2 代入上式,得
2 = -4k
解得
(2)当 x=6 时, y = -3.
已知y是x的正比例函数,且当x=-4时,y=2。
(1)求y与x之间的函数解析式。
(2)当x=6时,求函数y的值。
设
代
求
写
待定系数法
所以y与x之间的函数解析式为 y= - x
例
2
1
k= -
探究(二)
例2.列式表示下列问题中变量之间的函数关系,并判断是不是正比例函数.
(1)圆的周长l 随半径r的变化而变化.
典例分析
(2)冷冻一个0℃的物体,使它每分钟下降2℃,物体温度T(单位:℃)随冷冻时间t(单位:min)的变化而变化.
是正比例函数,比例系数为2π
T=-2t
是正比例函数,比例系数为-2
(r>0)
(t≥0)
课堂测试
下列说法正确的打“√”,错误的打“×”
(1)若y=kx,则y是x的正比例函数( )
(2)若y=3x2,则y是x的正比例函数( )
(3)若y=2(x-2)+4,则y是x的正比例函数( )
(4)若y=7(x-1) ,则y是x-1的正比例函数( )
这节课我学会(懂得)了……
总结归纳
正比例函数解析式y=kx(k≠0)的结构特征:
k是常数,k≠0
自变量x的次数是1
k与x是乘积关系 y=kx,称y与x成正比例,反之,
若y与x成正比例,可以设 y=kx
正比例函数解析式的一般式:
(k是常数,k≠0)
y = k · x
x的指数是1。
所以自变量 x 的次数为 1,即 a-2=1.
解得:a=3.
探索与思考
画出下列正比例函数的图像
1)y=2x,y=x
2)y=-1.5x,y=-4x
提示:列表—描点—连线
x -2 -1 0 1 2
y 3 1.5 0 -1.5 -3
2)函数y=-1.5x
函数y=-4x
x -2 -1 0 1 2
y 8 4 0 -4 -8
y=-1.5x
y=-4x
观察与思考
y=-1.5x
y=-4x
对一般正比例函数y =kx,当k < 0时,
(1)它的图象形状是什么?
(2)经过哪个象限?
(3)变化趋势怎样
(4)经过哪些特殊点
(5)哪个陡,哪个平缓
直线
二、四象限
y随x的增加而减小
经过原点(0,0)
k越大越缓
探究新知
(一)请画出下列函数的图像
x
1
2
3
4
-1
-2
-3
-4
y
1
2
3
4
-1
-2
-3
-4
1、图像是一条直线;
2、图像经过一、三象限;
3、图像从左往右依次上升;
4、y随x的增大而增大。
3. 点P(-1,3)在正比例函数y=kx的图像上,
则k的 值为_________.
K=-3
例题精讲
例1、已知正比例函数y=(1-2a)x
(1)若函数的图像经过原点和第一、三象限,则a的取值范围是多少?
理解正比例函数的性质
已知y=(k﹣3)是关于x的正比例函数,
(1)写出y与x之间的函数解析式:
(2)求当x=﹣4时,y的值.
【详解】
(1)当k2﹣8=1,且k﹣3≠0时,y是x的正比例函数,
故k=﹣3时,y是x的正比例函数,
∴y=﹣6x;
(2)当x=﹣4时,y=﹣6×(﹣4)=24.
理解正比例函数的概念
在 y=5x+2-a 中,若是 的正比例函数,则常数 _____.
【详解】解:因为是 的正比例函数,则a-2=0,a=2
小结
正比例函数
定义
注意
一般地,形如y=kx(k是常数, k≠0)的函数,叫做正比例函数, 其中 k 叫做比例系数.
①比例系数 k 是常数,且 k≠0;
②两个变量 x、y 的次数都是1.
待定系数法求解析式
一设
二列
三解
四写
聪明出于勤奋,天才在于积累。
