人教版数学八年级下册 20 复习与测试 课件(共22张PPT)
文档属性
| 名称 | 人教版数学八年级下册 20 复习与测试 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 07:16:25 | ||
图片预览







文档简介
(共22张PPT)
复习与测试
目录
01
教学目标
02
知识点框架
03
例题练习
04
作业布置
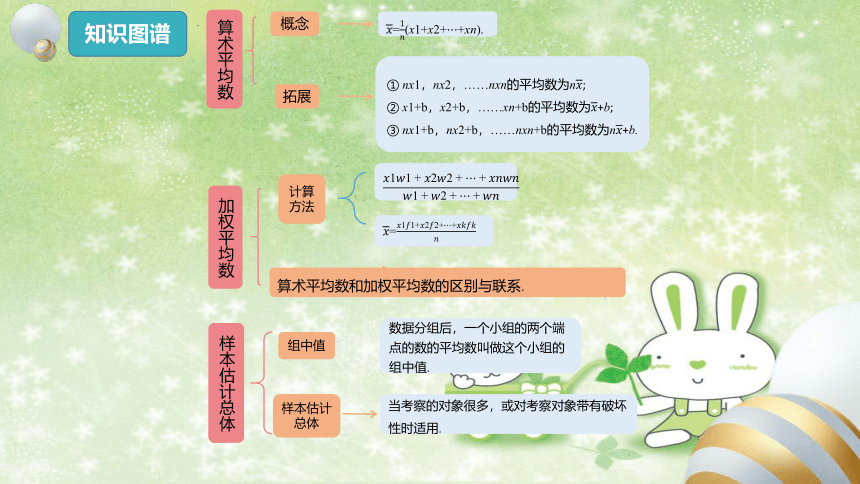
算术平均数
概念
拓展
=(x1+x2+ +xn).
① nx1,nx2,……nxn的平均数为n;
② x1+b,x2+b,……xn+b的平均数为+b;
③ nx1+b,nx2+b,……nxn+b的平均数为n+b.
知识图谱
加权平均数
计算
方法
算术平均数和加权平均数的区别与联系.
=
样本估计总体
组中值
样本估计总体
数据分组后,一个小组的两个端点的数的平均数叫做这个小组的组中值.
当考察的对象很多,或对考察对象带有破坏性时适用.
知识图谱
方差
估算
意义
用样本的方差估计总体的方差.
根据方差的大小来判断总体的稳定情况.
例题练习
03
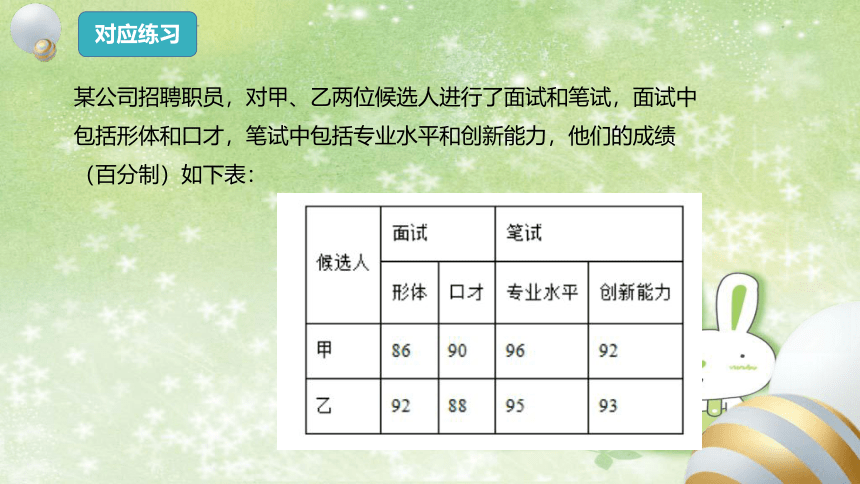
某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力,他们的成绩(百分制)如下表:
对应练习
例题
例7某教师就中学生对课外数阅读状况进行了一次问卷调查,并根据调查结果绘制了中学生每学期阅读课外书籍数量的统计图(不完整).设x表示阅读书籍的数量(x为正整数,单位:本),其中A:1≤x≤2;B:3≤x≤4;C:5≤x≤6;D:x≥7.请你根据两幅图提供的信息解答下列问题:
(1)本次共调查了多少名学生?
(2)补全条形统计图,并判断中位数在哪一组;
(3)计算扇形统计图中扇形D的圆心角的度数.
知识梳理
用样本平均数估计总体平均数
(1)组中值:数据分组后,一个小组的两个端点的数的平均数叫做这个小组的组中值.
(2)用样本的平均数估计总体的平均数:当要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.
练习
为了倡导“节约用水,从我做起”,黄冈市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果制成了如图所示的条形统计图.
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数;
(3)根据样本数据,估计黄冈市直机关500户家庭中月平均
用水量不超过12吨的约有多少户?
知识梳理
中位数
将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
对应练习
1.某课外学习小组有5人,在一次数学测验中的成绩分别是:120,100,135,100,125,则他们的成绩的平均数和众数分别是( )
A.116和100 B.116和125 C.106和120 D.106和135
A
2.某校对部分参加研学活动的中学生的年龄(单位:岁)进行统计,结果如表:
则这些学生年龄的众数和中位数分别是( )
A.15,15 B.15,13 C.15,14 D.14,15
A
知识梳理
用样本方差估计总体方差
用样本估计总体是统计的基本思想,类似于用样本的平均数估计总体的平均数,考察总体方差的时候,如果考察的总体包含很多个体,或者考察本身带有破坏性,实际中常常会用样本的方差来估计总体的方差.
作业布置
某老师为了了解学生周末利用网络进行学习的时间,在所任教班级随机调查了10名学生,其统计数据如表:
则这10名学生周末利用网络进行学均时间是 小时.
如图,四边形ABCD是等腰梯形,∠ABC=60°,若其四边满足长度的众数为5,平均数为6.25,上、下底之比为1:2,则BD= .
时间(单位:小时) 4 3 2 1 0
人数 2 4 2 1 1
感谢您的聆听
复习与测试
目录
01
教学目标
02
知识点框架
03
例题练习
04
作业布置
算术平均数
概念
拓展
=(x1+x2+ +xn).
① nx1,nx2,……nxn的平均数为n;
② x1+b,x2+b,……xn+b的平均数为+b;
③ nx1+b,nx2+b,……nxn+b的平均数为n+b.
知识图谱
加权平均数
计算
方法
算术平均数和加权平均数的区别与联系.
=
样本估计总体
组中值
样本估计总体
数据分组后,一个小组的两个端点的数的平均数叫做这个小组的组中值.
当考察的对象很多,或对考察对象带有破坏性时适用.
知识图谱
方差
估算
意义
用样本的方差估计总体的方差.
根据方差的大小来判断总体的稳定情况.
例题练习
03
某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力,他们的成绩(百分制)如下表:
对应练习
例题
例7某教师就中学生对课外数阅读状况进行了一次问卷调查,并根据调查结果绘制了中学生每学期阅读课外书籍数量的统计图(不完整).设x表示阅读书籍的数量(x为正整数,单位:本),其中A:1≤x≤2;B:3≤x≤4;C:5≤x≤6;D:x≥7.请你根据两幅图提供的信息解答下列问题:
(1)本次共调查了多少名学生?
(2)补全条形统计图,并判断中位数在哪一组;
(3)计算扇形统计图中扇形D的圆心角的度数.
知识梳理
用样本平均数估计总体平均数
(1)组中值:数据分组后,一个小组的两个端点的数的平均数叫做这个小组的组中值.
(2)用样本的平均数估计总体的平均数:当要考察的对象很多,或者对考察对象带有破坏性时,统计中常常通过用样本估计总体的方法来获得对总体的认识.
练习
为了倡导“节约用水,从我做起”,黄冈市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果制成了如图所示的条形统计图.
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数;
(3)根据样本数据,估计黄冈市直机关500户家庭中月平均
用水量不超过12吨的约有多少户?
知识梳理
中位数
将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
对应练习
1.某课外学习小组有5人,在一次数学测验中的成绩分别是:120,100,135,100,125,则他们的成绩的平均数和众数分别是( )
A.116和100 B.116和125 C.106和120 D.106和135
A
2.某校对部分参加研学活动的中学生的年龄(单位:岁)进行统计,结果如表:
则这些学生年龄的众数和中位数分别是( )
A.15,15 B.15,13 C.15,14 D.14,15
A
知识梳理
用样本方差估计总体方差
用样本估计总体是统计的基本思想,类似于用样本的平均数估计总体的平均数,考察总体方差的时候,如果考察的总体包含很多个体,或者考察本身带有破坏性,实际中常常会用样本的方差来估计总体的方差.
作业布置
某老师为了了解学生周末利用网络进行学习的时间,在所任教班级随机调查了10名学生,其统计数据如表:
则这10名学生周末利用网络进行学均时间是 小时.
如图,四边形ABCD是等腰梯形,∠ABC=60°,若其四边满足长度的众数为5,平均数为6.25,上、下底之比为1:2,则BD= .
时间(单位:小时) 4 3 2 1 0
人数 2 4 2 1 1
感谢您的聆听
