2.5《实验:用单摆测量重力加速度》(共43张ppt)
文档属性
| 名称 | 2.5《实验:用单摆测量重力加速度》(共43张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-27 09:27:38 | ||
图片预览









文档简介
(共43张PPT)
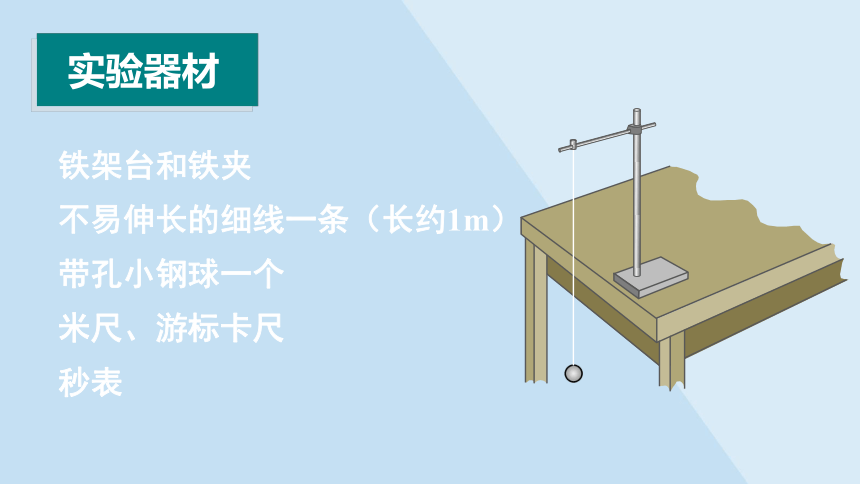
实验器材
铁架台和铁夹
不易伸长的细线一条(长约1m)
带孔小钢球一个
米尺、游标卡尺
秒表
1. 做单摆:取约1米长的线绳穿过带孔的小钢球,并打一个比小孔大一些的结,然后用夹子固定在桌边的铁架台上。
2. 测摆长:用米尺量出悬线长l,准确到毫米,用游标卡尺测摆球直径,算出半径r,也准确到毫米,则摆长为l+r 。
实验步骤
3. 测周期:把单摆从平衡位置拉开一个角度(<10 )放开它,用秒表测量单摆完成30次全振动(或50次)所用的时间t,求出完成一次全振动所需要的时间,这个平均时间就是单摆的周期。T= t / n
4. 求重力加速度:把测得的周期和摆长的数值代入公式,求出重力加速度g的值来。
5. 多次测量求平均值:改变摆长,重做几次实验。计算出每次实验的重力加速度。最后求出几次实验得到的重力加速度的平均值,即可看作本地区的重力加速度。
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
2分7.6秒
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
1分51.4秒
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
数据处理
1. 公式法(平均值法)
2. 图像法
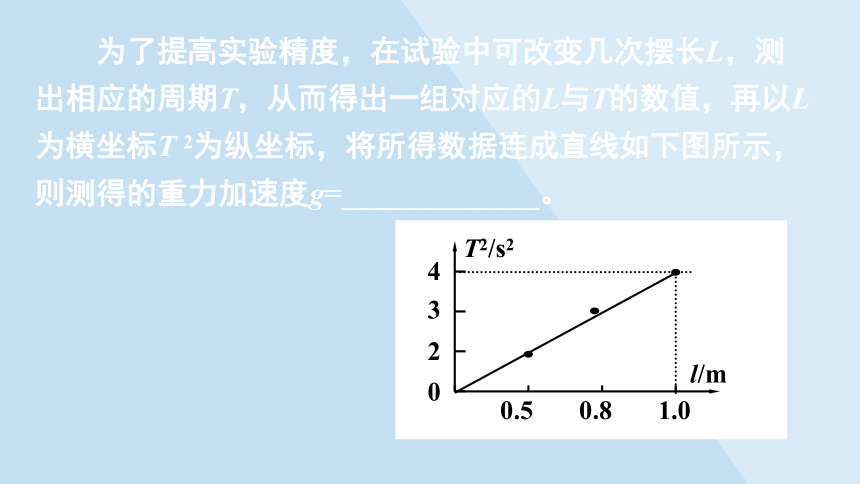
为了提高实验精度,在试验中可改变几次摆长L,测出相应的周期T,从而得出一组对应的L与T的数值,再以L为横坐标T 2为纵坐标,将所得数据连成直线如下图所示,则测得的重力加速度g=_____________。
l/m
1.0
0.8
0.5
T2/s2
4
3
2
0
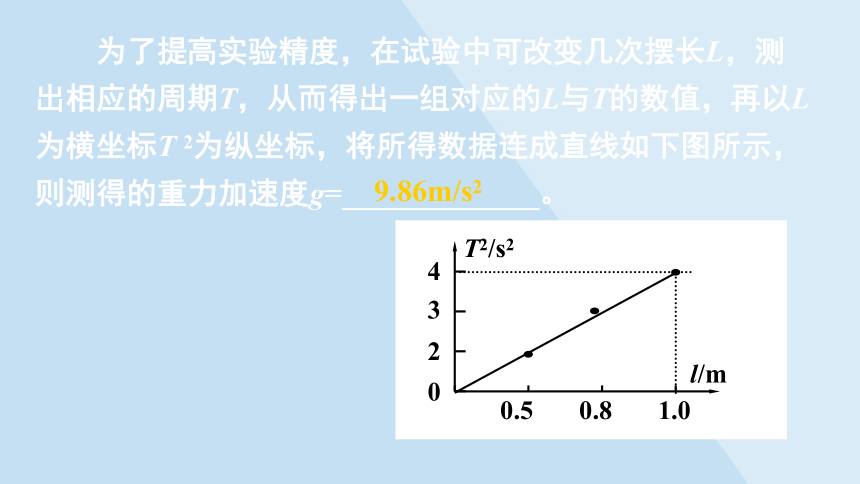
为了提高实验精度,在试验中可改变几次摆长L,测出相应的周期T,从而得出一组对应的L与T的数值,再以L为横坐标T 2为纵坐标,将所得数据连成直线如下图所示,则测得的重力加速度g=_____________。
9.86m/s2
l/m
1.0
0.8
0.5
T2/s2
4
3
2
0
1. 选择材料时应选择细轻又不易伸长的线,长度一般在1m左右,小球应选用密度较大的金属球,直径应较小,最好不超过2cm;
2. 单摆悬线的上端不可随意卷在铁夹的杆上,应夹紧在铁夹中,以免摆动时发生摆线下滑或悬点不固定,摆长改变的现象;
注意事项
3. 注意摆动时摆角不易过大,不能超过10 ,以保证单摆做简谐运动;
4. 摆球摆动时,要使之保持在同一个竖直平面内,不要形成圆锥摆;
5. 测量从球通过平衡位置时开始计时,因为在此位置摆球速度最大,易于分辨小球过此位置的时刻。
6. 为了减少偶然误差改变摆长,多次测量求平均值。
反思改进
在用单摆测量重力加速度时,若所用的摆球质量分布不均匀,不能用摆线长加球半径得到单摆的摆长。我们采用如下方法解决这个问题:
反思改进
在用单摆测量重力加速度时,若所用的摆球质量分布不均匀,不能用摆线长加球半径得到单摆的摆长。我们采用如下方法解决这个问题:
由①②两式可求得当地的重力加速度
【例题1】某同学用实验的方法探究影响单摆周期的因素。
(2) 他组装好单摆后在摆球自然悬垂的情况下,用毫米刻度尺从悬点量到摆球的最低端的长度L=0.9990m,再用游标卡尺测量摆球直径,结果如图所示,则该摆球的直径为_________mm,单摆摆长为_________m。
【例题1】某同学用实验的方法探究影响单摆周期的因素。
(2) 他组装好单摆后在摆球自然悬垂的情况下,用毫米刻度尺从悬点量到摆球的最低端的长度L=0.9990m,再用游标卡尺测量摆球直径,结果如图所示,则该摆球的直径为_________mm,单摆摆长为_________m。
12.0
【例题1】某同学用实验的方法探究影响单摆周期的因素。
(2) 他组装好单摆后在摆球自然悬垂的情况下,用毫米刻度尺从悬点量到摆球的最低端的长度L=0.9990m,再用游标卡尺测量摆球直径,结果如图所示,则该摆球的直径为_________mm,单摆摆长为_________m。
12.0
0.9930
【例题1】某同学用实验的方法探究影响单摆周期的因素。
(3) 下列振动图像真实地描述了对摆长约为1m的单摆进行周期测量的四种操作过程,图中横坐标原点表示计时开始,A、B、C均为30次全振动的图像,已知sin5°=0.087,sin15°=0.26,这四种操作过程合乎实验要求且误差最小的是______。(选填字母代号)
【例题1】某同学用实验的方法探究影响单摆周期的因素。
(3) 下列振动图像真实地描述了对摆长约为1m的单摆进行周期测量的四种操作过程,图中横坐标原点表示计时开始,A、B、C均为30次全振动的图像,已知sin5°=0.087,sin15°=0.26,这四种操作过程合乎实验要求且误差最小的是______。(选填字母代号)
A
变式训练1 在“探究单摆周期 与摆长的关系”实验中:
(1) 图1操作中正确的是________ (选填选项前的字母).
A. 甲图:小球从偏离平衡位置60°开始摆动
B. 乙图:细线上端用铁夹固定住
C. 丙图:小球到达最高点时作为计时开始与终止位置
D. 丁图:小球自由下垂时测量摆长
变式训练1 在“探究单摆周期 与摆长的关系”实验中:
(1) 图1操作中正确的是________ (选填选项前的字母).
A. 甲图:小球从偏离平衡位置60°开始摆动
B. 乙图:细线上端用铁夹固定住
C. 丙图:小球到达最高点时作为计时开始与终止位置
D. 丁图:小球自由下垂时测量摆长
BD
(2) 实验过程中,改变摆长,测量多组不同摆长情况下单摆的周期,以摆长为横坐标,周期的平方T2为纵坐标,作出了T2-l图像,理论上T2-l图线是一条过坐标原点的直线,但小周同学根据实验数据作出的图线如图2所示,则造成图线不过坐标原点的原因可能是________________________;由图像求出的重力加速度g=________m/s2.(取π2=9.86)
(2) 实验过程中,改变摆长,测量多组不同摆长情况下单摆的周期,以摆长为横坐标,周期的平方T2为纵坐标,作出了T2-l图像,理论上T2-l图线是一条过坐标原点的直线,但小周同学根据实验数据作出的图线如图2所示,则造成图线不过坐标原点的原因可能是________________________;由图像求出的重力加速度g=________m/s2.(取π2=9.86)
计算摆长时漏加小球半径
(2) 实验过程中,改变摆长,测量多组不同摆长情况下单摆的周期,以摆长为横坐标,周期的平方T2为纵坐标,作出了T2-l图像,理论上T2-l图线是一条过坐标原点的直线,但小周同学根据实验数据作出的图线如图2所示,则造成图线不过坐标原点的原因可能是________________________;由图像求出的重力加速度g=________m/s2.(取π2=9.86)
9.86
计算摆长时漏加小球半径
【例题2】在“利用单摆测重力加速度”的实验中:
(1) 某同学尝试用DIS测量周期。如图,用一个 磁性小球代替原先的摆球,在单摆下方放置一个磁 传感器,其轴线恰好位于单摆悬挂点正下方。图中 磁传感器的引出端A应接到______________。
使单摆做小角度摆动,当磁感应强度测量值最大时, 磁性小球位于___________________。若测得连续 N个磁感应强度最大值之间的时间间隔为t,则单摆 周期的测量值为________(地磁场和磁传感器的影 响可忽略)。
【例题2】在“利用单摆测重力加速度”的实验中:
(1) 某同学尝试用DIS测量周期。如图,用一个 磁性小球代替原先的摆球,在单摆下方放置一个磁 传感器,其轴线恰好位于单摆悬挂点正下方。图中 磁传感器的引出端A应接到______________。
使单摆做小角度摆动,当磁感应强度测量值最大时, 磁性小球位于___________________。若测得连续 N个磁感应强度最大值之间的时间间隔为t,则单摆 周期的测量值为________(地磁场和磁传感器的影 响可忽略)。
数据采集器
【例题2】在“利用单摆测重力加速度”的实验中:
(1) 某同学尝试用DIS测量周期。如图,用一个 磁性小球代替原先的摆球,在单摆下方放置一个磁 传感器,其轴线恰好位于单摆悬挂点正下方。图中 磁传感器的引出端A应接到______________。
使单摆做小角度摆动,当磁感应强度测量值最大时, 磁性小球位于___________________。若测得连续 N个磁感应强度最大值之间的时间间隔为t,则单摆 周期的测量值为________(地磁场和磁传感器的影 响可忽略)。
数据采集器
最低点(平衡位置)
【例题2】在“利用单摆测重力加速度”的实验中:
(1) 某同学尝试用DIS测量周期。如图,用一个 磁性小球代替原先的摆球,在单摆下方放置一个磁 传感器,其轴线恰好位于单摆悬挂点正下方。图中 磁传感器的引出端A应接到______________。
使单摆做小角度摆动,当磁感应强度测量值最大时, 磁性小球位于___________________。若测得连续 N个磁感应强度最大值之间的时间间隔为t,则单摆 周期的测量值为________(地磁场和磁传感器的影 响可忽略)。
数据采集器
最低点(平衡位置)
直线
直线
【例题3】在“用单摆测定重力加速度”的实验中:
(1) 用二十分度的游标卡尺测量摆球直径的结果如图所示。则小球的直径为__________mm。
(2) 为了减小测量周期的误差,摆球应在经过最_________(选填“高”或“低”)点的位置时开始计时,并用秒表测量单摆完成多次全振动所用的时间求出周期。 (3) 若用L表示摆长,单摆完成30次全振动所用时间为t,那么重力加速度的表达式为g=_____________。
【例题3】在“用单摆测定重力加速度”的实验中:
(1) 用二十分度的游标卡尺测量摆球直径的结果如图所示。则小球的直径为__________mm。
17.15
(2) 为了减小测量周期的误差,摆球应在经过最_________(选填“高”或“低”)点的位置时开始计时,并用秒表测量单摆完成多次全振动所用的时间求出周期。 (3) 若用L表示摆长,单摆完成30次全振动所用时间为t,那么重力加速度的表达式为g=_____________。
【例题3】在“用单摆测定重力加速度”的实验中:
(1) 用二十分度的游标卡尺测量摆球直径的结果如图所示。则小球的直径为__________mm。
17.15
(2) 为了减小测量周期的误差,摆球应在经过最_________(选填“高”或“低”)点的位置时开始计时,并用秒表测量单摆完成多次全振动所用的时间求出周期。 (3) 若用L表示摆长,单摆完成30次全振动所用时间为t,那么重力加速度的表达式为g=_____________。
低
【例题3】在“用单摆测定重力加速度”的实验中:
(1) 用二十分度的游标卡尺测量摆球直径的结果如图所示。则小球的直径为__________mm。
17.15
(2) 为了减小测量周期的误差,摆球应在经过最_________(选填“高”或“低”)点的位置时开始计时,并用秒表测量单摆完成多次全振动所用的时间求出周期。 (3) 若用L表示摆长,单摆完成30次全振动所用时间为t,那么重力加速度的表达式为g=_____________。
低
变式训练2 在“探究单摆周期与摆长的关系”的实验中:
(1) 选择好器材,将符合实验要求的单摆悬挂在铁架台上,应采用图________中所示的固定方式.
变式训练2 在“探究单摆周期与摆长的关系”的实验中:
(1) 选择好器材,将符合实验要求的单摆悬挂在铁架台上,应采用图________中所示的固定方式.
乙
(2)需要测量悬线长度,现用最小分度为1 mm的米尺测量,图丙中箭头所指位置是拉直的悬线两端在米尺上相对应的位置,测得悬线长度为__________mm;如图丁,用游标卡尺测量小球的直径如图丁所示,则该单摆的摆长为L=____________mm.
(3)在做“用单摆测定重力加速度”的实验时,用摆长L和周期T计算重力加速度的公式是g=________.
(2)需要测量悬线长度,现用最小分度为1 mm的米尺测量,图丙中箭头所指位置是拉直的悬线两端在米尺上相对应的位置,测得悬线长度为__________mm;如图丁,用游标卡尺测量小球的直径如图丁所示,则该单摆的摆长为L=____________mm.
(3)在做“用单摆测定重力加速度”的实验时,用摆长L和周期T计算重力加速度的公式是g=________.
987.0
(2)需要测量悬线长度,现用最小分度为1 mm的米尺测量,图丙中箭头所指位置是拉直的悬线两端在米尺上相对应的位置,测得悬线长度为__________mm;如图丁,用游标卡尺测量小球的直径如图丁所示,则该单摆的摆长为L=____________mm.
(3)在做“用单摆测定重力加速度”的实验时,用摆长L和周期T计算重力加速度的公式是g=________.
987.0
994.1
(2)需要测量悬线长度,现用最小分度为1 mm的米尺测量,图丙中箭头所指位置是拉直的悬线两端在米尺上相对应的位置,测得悬线长度为__________mm;如图丁,用游标卡尺测量小球的直径如图丁所示,则该单摆的摆长为L=____________mm.
(3)在做“用单摆测定重力加速度”的实验时,用摆长L和周期T计算重力加速度的公式是g=________.
987.0
994.1
实验器材
铁架台和铁夹
不易伸长的细线一条(长约1m)
带孔小钢球一个
米尺、游标卡尺
秒表
1. 做单摆:取约1米长的线绳穿过带孔的小钢球,并打一个比小孔大一些的结,然后用夹子固定在桌边的铁架台上。
2. 测摆长:用米尺量出悬线长l,准确到毫米,用游标卡尺测摆球直径,算出半径r,也准确到毫米,则摆长为l+r 。
实验步骤
3. 测周期:把单摆从平衡位置拉开一个角度(<10 )放开它,用秒表测量单摆完成30次全振动(或50次)所用的时间t,求出完成一次全振动所需要的时间,这个平均时间就是单摆的周期。T= t / n
4. 求重力加速度:把测得的周期和摆长的数值代入公式,求出重力加速度g的值来。
5. 多次测量求平均值:改变摆长,重做几次实验。计算出每次实验的重力加速度。最后求出几次实验得到的重力加速度的平均值,即可看作本地区的重力加速度。
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
2分7.6秒
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
1分51.4秒
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
数据处理
1. 公式法(平均值法)
2. 图像法
为了提高实验精度,在试验中可改变几次摆长L,测出相应的周期T,从而得出一组对应的L与T的数值,再以L为横坐标T 2为纵坐标,将所得数据连成直线如下图所示,则测得的重力加速度g=_____________。
l/m
1.0
0.8
0.5
T2/s2
4
3
2
0
为了提高实验精度,在试验中可改变几次摆长L,测出相应的周期T,从而得出一组对应的L与T的数值,再以L为横坐标T 2为纵坐标,将所得数据连成直线如下图所示,则测得的重力加速度g=_____________。
9.86m/s2
l/m
1.0
0.8
0.5
T2/s2
4
3
2
0
1. 选择材料时应选择细轻又不易伸长的线,长度一般在1m左右,小球应选用密度较大的金属球,直径应较小,最好不超过2cm;
2. 单摆悬线的上端不可随意卷在铁夹的杆上,应夹紧在铁夹中,以免摆动时发生摆线下滑或悬点不固定,摆长改变的现象;
注意事项
3. 注意摆动时摆角不易过大,不能超过10 ,以保证单摆做简谐运动;
4. 摆球摆动时,要使之保持在同一个竖直平面内,不要形成圆锥摆;
5. 测量从球通过平衡位置时开始计时,因为在此位置摆球速度最大,易于分辨小球过此位置的时刻。
6. 为了减少偶然误差改变摆长,多次测量求平均值。
反思改进
在用单摆测量重力加速度时,若所用的摆球质量分布不均匀,不能用摆线长加球半径得到单摆的摆长。我们采用如下方法解决这个问题:
反思改进
在用单摆测量重力加速度时,若所用的摆球质量分布不均匀,不能用摆线长加球半径得到单摆的摆长。我们采用如下方法解决这个问题:
由①②两式可求得当地的重力加速度
【例题1】某同学用实验的方法探究影响单摆周期的因素。
(2) 他组装好单摆后在摆球自然悬垂的情况下,用毫米刻度尺从悬点量到摆球的最低端的长度L=0.9990m,再用游标卡尺测量摆球直径,结果如图所示,则该摆球的直径为_________mm,单摆摆长为_________m。
【例题1】某同学用实验的方法探究影响单摆周期的因素。
(2) 他组装好单摆后在摆球自然悬垂的情况下,用毫米刻度尺从悬点量到摆球的最低端的长度L=0.9990m,再用游标卡尺测量摆球直径,结果如图所示,则该摆球的直径为_________mm,单摆摆长为_________m。
12.0
【例题1】某同学用实验的方法探究影响单摆周期的因素。
(2) 他组装好单摆后在摆球自然悬垂的情况下,用毫米刻度尺从悬点量到摆球的最低端的长度L=0.9990m,再用游标卡尺测量摆球直径,结果如图所示,则该摆球的直径为_________mm,单摆摆长为_________m。
12.0
0.9930
【例题1】某同学用实验的方法探究影响单摆周期的因素。
(3) 下列振动图像真实地描述了对摆长约为1m的单摆进行周期测量的四种操作过程,图中横坐标原点表示计时开始,A、B、C均为30次全振动的图像,已知sin5°=0.087,sin15°=0.26,这四种操作过程合乎实验要求且误差最小的是______。(选填字母代号)
【例题1】某同学用实验的方法探究影响单摆周期的因素。
(3) 下列振动图像真实地描述了对摆长约为1m的单摆进行周期测量的四种操作过程,图中横坐标原点表示计时开始,A、B、C均为30次全振动的图像,已知sin5°=0.087,sin15°=0.26,这四种操作过程合乎实验要求且误差最小的是______。(选填字母代号)
A
变式训练1 在“探究单摆周期 与摆长的关系”实验中:
(1) 图1操作中正确的是________ (选填选项前的字母).
A. 甲图:小球从偏离平衡位置60°开始摆动
B. 乙图:细线上端用铁夹固定住
C. 丙图:小球到达最高点时作为计时开始与终止位置
D. 丁图:小球自由下垂时测量摆长
变式训练1 在“探究单摆周期 与摆长的关系”实验中:
(1) 图1操作中正确的是________ (选填选项前的字母).
A. 甲图:小球从偏离平衡位置60°开始摆动
B. 乙图:细线上端用铁夹固定住
C. 丙图:小球到达最高点时作为计时开始与终止位置
D. 丁图:小球自由下垂时测量摆长
BD
(2) 实验过程中,改变摆长,测量多组不同摆长情况下单摆的周期,以摆长为横坐标,周期的平方T2为纵坐标,作出了T2-l图像,理论上T2-l图线是一条过坐标原点的直线,但小周同学根据实验数据作出的图线如图2所示,则造成图线不过坐标原点的原因可能是________________________;由图像求出的重力加速度g=________m/s2.(取π2=9.86)
(2) 实验过程中,改变摆长,测量多组不同摆长情况下单摆的周期,以摆长为横坐标,周期的平方T2为纵坐标,作出了T2-l图像,理论上T2-l图线是一条过坐标原点的直线,但小周同学根据实验数据作出的图线如图2所示,则造成图线不过坐标原点的原因可能是________________________;由图像求出的重力加速度g=________m/s2.(取π2=9.86)
计算摆长时漏加小球半径
(2) 实验过程中,改变摆长,测量多组不同摆长情况下单摆的周期,以摆长为横坐标,周期的平方T2为纵坐标,作出了T2-l图像,理论上T2-l图线是一条过坐标原点的直线,但小周同学根据实验数据作出的图线如图2所示,则造成图线不过坐标原点的原因可能是________________________;由图像求出的重力加速度g=________m/s2.(取π2=9.86)
9.86
计算摆长时漏加小球半径
【例题2】在“利用单摆测重力加速度”的实验中:
(1) 某同学尝试用DIS测量周期。如图,用一个 磁性小球代替原先的摆球,在单摆下方放置一个磁 传感器,其轴线恰好位于单摆悬挂点正下方。图中 磁传感器的引出端A应接到______________。
使单摆做小角度摆动,当磁感应强度测量值最大时, 磁性小球位于___________________。若测得连续 N个磁感应强度最大值之间的时间间隔为t,则单摆 周期的测量值为________(地磁场和磁传感器的影 响可忽略)。
【例题2】在“利用单摆测重力加速度”的实验中:
(1) 某同学尝试用DIS测量周期。如图,用一个 磁性小球代替原先的摆球,在单摆下方放置一个磁 传感器,其轴线恰好位于单摆悬挂点正下方。图中 磁传感器的引出端A应接到______________。
使单摆做小角度摆动,当磁感应强度测量值最大时, 磁性小球位于___________________。若测得连续 N个磁感应强度最大值之间的时间间隔为t,则单摆 周期的测量值为________(地磁场和磁传感器的影 响可忽略)。
数据采集器
【例题2】在“利用单摆测重力加速度”的实验中:
(1) 某同学尝试用DIS测量周期。如图,用一个 磁性小球代替原先的摆球,在单摆下方放置一个磁 传感器,其轴线恰好位于单摆悬挂点正下方。图中 磁传感器的引出端A应接到______________。
使单摆做小角度摆动,当磁感应强度测量值最大时, 磁性小球位于___________________。若测得连续 N个磁感应强度最大值之间的时间间隔为t,则单摆 周期的测量值为________(地磁场和磁传感器的影 响可忽略)。
数据采集器
最低点(平衡位置)
【例题2】在“利用单摆测重力加速度”的实验中:
(1) 某同学尝试用DIS测量周期。如图,用一个 磁性小球代替原先的摆球,在单摆下方放置一个磁 传感器,其轴线恰好位于单摆悬挂点正下方。图中 磁传感器的引出端A应接到______________。
使单摆做小角度摆动,当磁感应强度测量值最大时, 磁性小球位于___________________。若测得连续 N个磁感应强度最大值之间的时间间隔为t,则单摆 周期的测量值为________(地磁场和磁传感器的影 响可忽略)。
数据采集器
最低点(平衡位置)
直线
直线
【例题3】在“用单摆测定重力加速度”的实验中:
(1) 用二十分度的游标卡尺测量摆球直径的结果如图所示。则小球的直径为__________mm。
(2) 为了减小测量周期的误差,摆球应在经过最_________(选填“高”或“低”)点的位置时开始计时,并用秒表测量单摆完成多次全振动所用的时间求出周期。 (3) 若用L表示摆长,单摆完成30次全振动所用时间为t,那么重力加速度的表达式为g=_____________。
【例题3】在“用单摆测定重力加速度”的实验中:
(1) 用二十分度的游标卡尺测量摆球直径的结果如图所示。则小球的直径为__________mm。
17.15
(2) 为了减小测量周期的误差,摆球应在经过最_________(选填“高”或“低”)点的位置时开始计时,并用秒表测量单摆完成多次全振动所用的时间求出周期。 (3) 若用L表示摆长,单摆完成30次全振动所用时间为t,那么重力加速度的表达式为g=_____________。
【例题3】在“用单摆测定重力加速度”的实验中:
(1) 用二十分度的游标卡尺测量摆球直径的结果如图所示。则小球的直径为__________mm。
17.15
(2) 为了减小测量周期的误差,摆球应在经过最_________(选填“高”或“低”)点的位置时开始计时,并用秒表测量单摆完成多次全振动所用的时间求出周期。 (3) 若用L表示摆长,单摆完成30次全振动所用时间为t,那么重力加速度的表达式为g=_____________。
低
【例题3】在“用单摆测定重力加速度”的实验中:
(1) 用二十分度的游标卡尺测量摆球直径的结果如图所示。则小球的直径为__________mm。
17.15
(2) 为了减小测量周期的误差,摆球应在经过最_________(选填“高”或“低”)点的位置时开始计时,并用秒表测量单摆完成多次全振动所用的时间求出周期。 (3) 若用L表示摆长,单摆完成30次全振动所用时间为t,那么重力加速度的表达式为g=_____________。
低
变式训练2 在“探究单摆周期与摆长的关系”的实验中:
(1) 选择好器材,将符合实验要求的单摆悬挂在铁架台上,应采用图________中所示的固定方式.
变式训练2 在“探究单摆周期与摆长的关系”的实验中:
(1) 选择好器材,将符合实验要求的单摆悬挂在铁架台上,应采用图________中所示的固定方式.
乙
(2)需要测量悬线长度,现用最小分度为1 mm的米尺测量,图丙中箭头所指位置是拉直的悬线两端在米尺上相对应的位置,测得悬线长度为__________mm;如图丁,用游标卡尺测量小球的直径如图丁所示,则该单摆的摆长为L=____________mm.
(3)在做“用单摆测定重力加速度”的实验时,用摆长L和周期T计算重力加速度的公式是g=________.
(2)需要测量悬线长度,现用最小分度为1 mm的米尺测量,图丙中箭头所指位置是拉直的悬线两端在米尺上相对应的位置,测得悬线长度为__________mm;如图丁,用游标卡尺测量小球的直径如图丁所示,则该单摆的摆长为L=____________mm.
(3)在做“用单摆测定重力加速度”的实验时,用摆长L和周期T计算重力加速度的公式是g=________.
987.0
(2)需要测量悬线长度,现用最小分度为1 mm的米尺测量,图丙中箭头所指位置是拉直的悬线两端在米尺上相对应的位置,测得悬线长度为__________mm;如图丁,用游标卡尺测量小球的直径如图丁所示,则该单摆的摆长为L=____________mm.
(3)在做“用单摆测定重力加速度”的实验时,用摆长L和周期T计算重力加速度的公式是g=________.
987.0
994.1
(2)需要测量悬线长度,现用最小分度为1 mm的米尺测量,图丙中箭头所指位置是拉直的悬线两端在米尺上相对应的位置,测得悬线长度为__________mm;如图丁,用游标卡尺测量小球的直径如图丁所示,则该单摆的摆长为L=____________mm.
(3)在做“用单摆测定重力加速度”的实验时,用摆长L和周期T计算重力加速度的公式是g=________.
987.0
994.1
