等腰三角形
图片预览










文档简介
课件34张PPT。热烈欢迎各位领导、各位
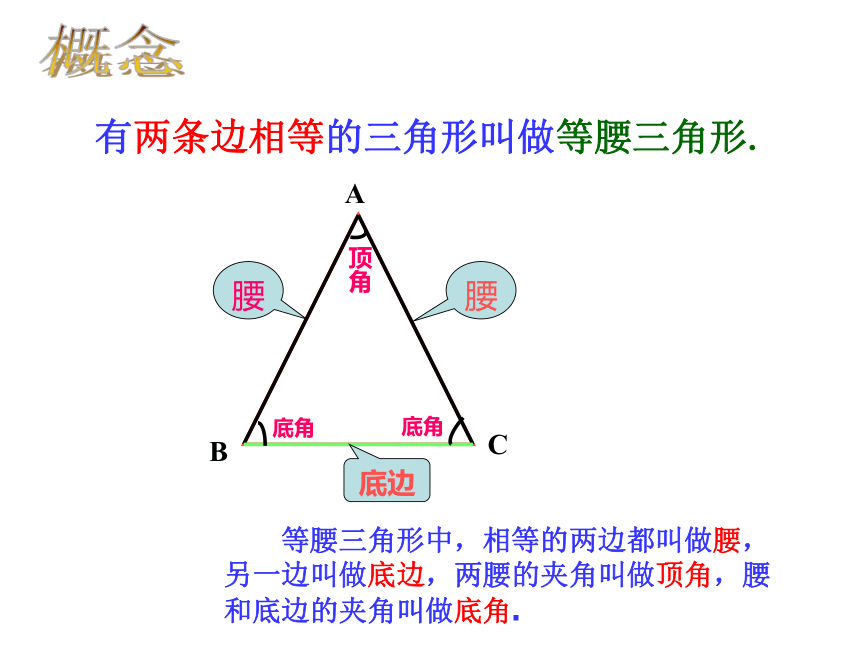
老师莅临我校指导工作!丰城市蕉坑初中 聂兴红精彩的世界细心观察细心观察细心观察下载图片12.3.1等腰三角形蕉坑中学 聂兴红有两条边相等的三角形叫做等腰三角形. 等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.底边概念复习提问: 一般三角形的性质: A. 三角形三边关系是什么?B. 三角形三个内角间的关系是什么?C.三角形内外角间的关系是什么?等腰三角形具有一般三角形的所有性质 1、等腰三角形一腰为3cm,底为4cm,则它的周长
是 ;
2、等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是 ;
3、等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
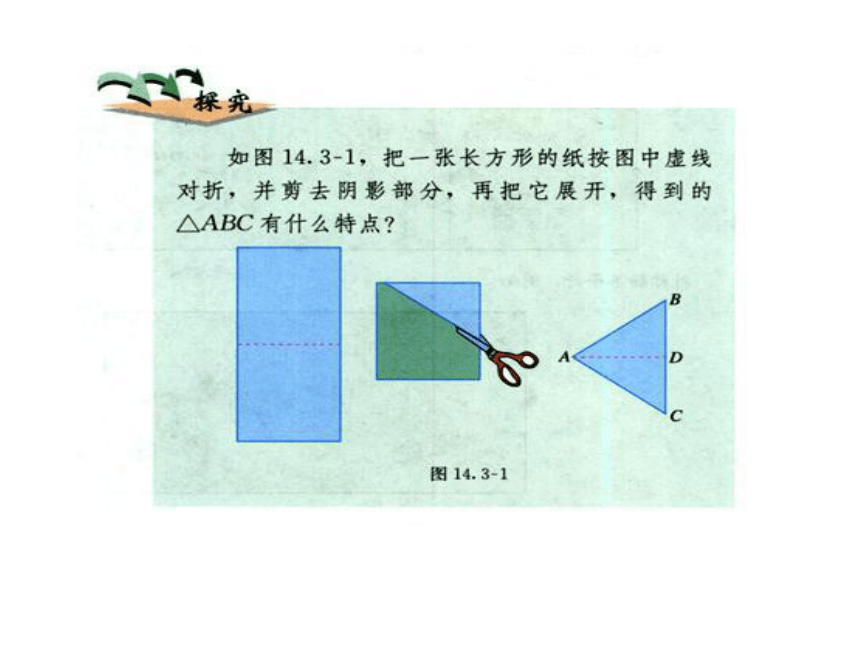
10 cm10 cm 或 11 cm19 cm小试牛刀如图,把一张长方形的纸按图中虚线对折, 并剪去绿色部分, 再把它展开,得到的△ABC有什么特点?ABCAB=AC等腰三角形活动(一):动手操作 等腰三角形是轴对称图形吗?
思考是ABCD把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角,填入下表: 等腰三角形除了两腰相等以外,你还能发现它的其他性质吗?
AB=ACBD=CDAD=AD∠B=∠C∠ADB=∠ADC∠BAD=∠CAD活动(二):细心观察 大胆猜想等腰三角形的两个底角相等。已知:△ABC中,AB=AC求证:∠B=?C想一想:1.如何证明两个角相等? 议一议:2.如何构造两个全等的三 角形?活动(三):小组讨论已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.等腰三角形的两个底角相等。D证明: 作底边的中线AD,则BD=CDAB=AC ( 已知 )BD=CD ( 已作 )AD=AD (公共边) ∴ △BAD ≌ △CAD (SSS).∴ ∠ B= ∠C (全等三角形的对应角相等).在△BAD和△CAD中方法一:作底边上的中线等腰三角形的性质: 性质1:等腰三角形的两个底角相等 (简写“等边对等角”)在△ABC中∵AB=AC∠B=∠C (等边对等角)注意:
在一个 三角形中,等边对等角.已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.等腰三角形的两个底角相等。D证明: 作顶角的平分线AD,则∠1=∠2AB=AC ( 已知 )∠1=∠2 ( 已作 )AD=AD (公共边) ∴ △BAD ≌ △CAD (SAS).∴ ∠ B= ∠C (全等三角形的对应角相等).方法二:作顶角的平分线在△BAD和△CAD中12已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.等腰三角形的两个底角相等。D证明: 作底边的高线AD,则∠BDA=∠CDA=90°AB=AC ( 已知 )AD=AD (公共边) ∴ Rt△BAD ≌ Rt△CAD (HL).∴ ∠ B= ∠C (全等三角形的对应角相等).方法三:作底边的高线在Rt△BAD和Rt△CAD中猜想一:等腰直角三角形每一个底角为_____ __;
45°.猜想二:等边三角形每一个角为_____ .
60°⒈等腰三角形一个底角为75°,它的另外两个
角为_____ __;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个角
为______ __。75°, 30°70°,40°或55°,55°35°,35°小试牛刀(等腰三角形三线合一)性质2 等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合活动(四):小组讨论思考:
由△BAD ≌ △CAD,除了可以得到∠ B= ∠C之外,你还可以得到那些相等的线段和相等的角?和你的同伴交流一下,看看你有什么新的发现?
性质3 等腰三角形是轴对称图形,其顶角的平分线(底边上的中线、底边上的高)所在的直线就是等腰三角形的对称轴。“三线合一”的操作在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____. 等腰三角形“三线合一”的性质用符号语言表示为:12BDCD12ADBCADBCBDCD例1、如图,在△ABC中 ,AB=AC,点D在AC上,且 BD=BC=AD,求△ABC各角的度数。解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD (等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中, ∠A=36.∠ABC=∠C=72°例2、如图在△ABC中,AB=AC, 点D、E在BC上,且AD=AE, 求证:BD=CE证明一:作AH ⊥BC于H
∵ AB=AC ∴ BH=CH (三线合一)
∵ AD=AE ∴ DH=EH(三线合一)
∴ BH-DH=CH-EH
∴ BD=CE总结:此题运用“三线合一”性质和等式性质解决。证明二:略1、如图,△ABC是等腰直角三角形,(AB=AC, ∠BAC=90°),AD是底边BC上的高,
求出∠B 、∠C 、∠BAD 、∠DAC的度数,图中有哪些相等的线段?
2、如图在△ABC中,AB=AD=DC, ∠BAD=26°,
求∠B和∠C答案:1、∠B=∠C=∠BAD=∠DAC=45° AB=AC BD=CD=AD
2、∠B=77° ∠C=38.5°大展身手(1)本节课里你学到了什么???(2)等腰三角形中常作的辅助线:作顶角的平分线、底边上的高或底边上的中线共同回顾活动(五):作业: 教科书习题12.3
第1、4、13题
如图在△ABC中,∠B=∠C
思考能否推出△ABC是等腰三角形呢?谢 谢 指 导!
老师莅临我校指导工作!丰城市蕉坑初中 聂兴红精彩的世界细心观察细心观察细心观察下载图片12.3.1等腰三角形蕉坑中学 聂兴红有两条边相等的三角形叫做等腰三角形. 等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.底边概念复习提问: 一般三角形的性质: A. 三角形三边关系是什么?B. 三角形三个内角间的关系是什么?C.三角形内外角间的关系是什么?等腰三角形具有一般三角形的所有性质 1、等腰三角形一腰为3cm,底为4cm,则它的周长
是 ;
2、等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是 ;
3、等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
10 cm10 cm 或 11 cm19 cm小试牛刀如图,把一张长方形的纸按图中虚线对折, 并剪去绿色部分, 再把它展开,得到的△ABC有什么特点?ABCAB=AC等腰三角形活动(一):动手操作 等腰三角形是轴对称图形吗?
思考是ABCD把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角,填入下表: 等腰三角形除了两腰相等以外,你还能发现它的其他性质吗?
AB=ACBD=CDAD=AD∠B=∠C∠ADB=∠ADC∠BAD=∠CAD活动(二):细心观察 大胆猜想等腰三角形的两个底角相等。已知:△ABC中,AB=AC求证:∠B=?C想一想:1.如何证明两个角相等? 议一议:2.如何构造两个全等的三 角形?活动(三):小组讨论已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.等腰三角形的两个底角相等。D证明: 作底边的中线AD,则BD=CDAB=AC ( 已知 )BD=CD ( 已作 )AD=AD (公共边) ∴ △BAD ≌ △CAD (SSS).∴ ∠ B= ∠C (全等三角形的对应角相等).在△BAD和△CAD中方法一:作底边上的中线等腰三角形的性质: 性质1:等腰三角形的两个底角相等 (简写“等边对等角”)在△ABC中∵AB=AC∠B=∠C (等边对等角)注意:
在一个 三角形中,等边对等角.已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.等腰三角形的两个底角相等。D证明: 作顶角的平分线AD,则∠1=∠2AB=AC ( 已知 )∠1=∠2 ( 已作 )AD=AD (公共边) ∴ △BAD ≌ △CAD (SAS).∴ ∠ B= ∠C (全等三角形的对应角相等).方法二:作顶角的平分线在△BAD和△CAD中12已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.等腰三角形的两个底角相等。D证明: 作底边的高线AD,则∠BDA=∠CDA=90°AB=AC ( 已知 )AD=AD (公共边) ∴ Rt△BAD ≌ Rt△CAD (HL).∴ ∠ B= ∠C (全等三角形的对应角相等).方法三:作底边的高线在Rt△BAD和Rt△CAD中猜想一:等腰直角三角形每一个底角为_____ __;
45°.猜想二:等边三角形每一个角为_____ .
60°⒈等腰三角形一个底角为75°,它的另外两个
角为_____ __;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个角
为______ __。75°, 30°70°,40°或55°,55°35°,35°小试牛刀(等腰三角形三线合一)性质2 等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合活动(四):小组讨论思考:
由△BAD ≌ △CAD,除了可以得到∠ B= ∠C之外,你还可以得到那些相等的线段和相等的角?和你的同伴交流一下,看看你有什么新的发现?
性质3 等腰三角形是轴对称图形,其顶角的平分线(底边上的中线、底边上的高)所在的直线就是等腰三角形的对称轴。“三线合一”的操作在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____. 等腰三角形“三线合一”的性质用符号语言表示为:12BDCD12ADBCADBCBDCD例1、如图,在△ABC中 ,AB=AC,点D在AC上,且 BD=BC=AD,求△ABC各角的度数。解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD (等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中, ∠A=36.∠ABC=∠C=72°例2、如图在△ABC中,AB=AC, 点D、E在BC上,且AD=AE, 求证:BD=CE证明一:作AH ⊥BC于H
∵ AB=AC ∴ BH=CH (三线合一)
∵ AD=AE ∴ DH=EH(三线合一)
∴ BH-DH=CH-EH
∴ BD=CE总结:此题运用“三线合一”性质和等式性质解决。证明二:略1、如图,△ABC是等腰直角三角形,(AB=AC, ∠BAC=90°),AD是底边BC上的高,
求出∠B 、∠C 、∠BAD 、∠DAC的度数,图中有哪些相等的线段?
2、如图在△ABC中,AB=AD=DC, ∠BAD=26°,
求∠B和∠C答案:1、∠B=∠C=∠BAD=∠DAC=45° AB=AC BD=CD=AD
2、∠B=77° ∠C=38.5°大展身手(1)本节课里你学到了什么???(2)等腰三角形中常作的辅助线:作顶角的平分线、底边上的高或底边上的中线共同回顾活动(五):作业: 教科书习题12.3
第1、4、13题
如图在△ABC中,∠B=∠C
思考能否推出△ABC是等腰三角形呢?谢 谢 指 导!
