2.2.2完全平方公式2
图片预览



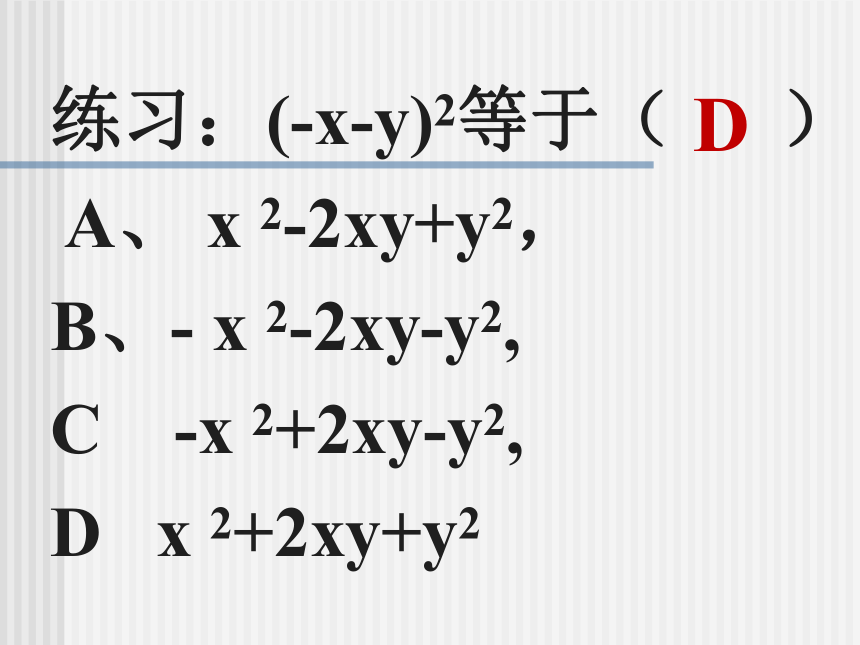

文档简介
课件10张PPT。完全平方公式(2) (a+b)2=a2+2ab+b2(a?b)2=a2?2ab+b2完全平方公式 和的完全平方公式与差的完全平方公式统称完全平方公式.
平方差公式和完全平方公式也称乘法公式。例:运用完全平方公式计算 (1)(-x+1)2 (2)(-2x-3)2解练习:(-x-y)2等于( )
A、 x 2-2xy+y2,
B、- x 2-2xy-y2,
C -x 2+2xy-y2,
D x 2+2xy+y2
D例 运用完全平方公式计算:(1)(a+b)2-(a-b)2
(2)(a+b+1)2应用完全平方公式进行数的计算 例:运用完全平方公式计算: 1042 ? ? 解:1042=(100+4)2
=1002+2×100×4+42
=10000+800+16
=10816
运用完全平方公式计算:1982 解 1982=(200-2)2
=2002-2×200×2+22
=40000-800+4
=39204
完全平方公式和平方差公式不同:形式不同:平方差公式是两数和与两数差的积
完全平方公式的两数和的平方结果不同:完全平方公式的结果 是三项,
即 (a ?b)2=a2 ?2ab+b2;平方差公式的结果 是两项,
即 (a+b)(a?b)=a2?b2.(1)化简: (2m+1)2 - (2m)2(3)用简便的方法计算: 23452+0.76552+2.469×0.7655做一做:(4)如果x2+ax+36是一个完全平方式,那么a=______(6)已知(a+b)2=11,ab=1,求(a-b)2的值.做一做:(5)如果x2+6x+b2是一个完全平方式,那么b= ;
平方差公式和完全平方公式也称乘法公式。例:运用完全平方公式计算 (1)(-x+1)2 (2)(-2x-3)2解练习:(-x-y)2等于( )
A、 x 2-2xy+y2,
B、- x 2-2xy-y2,
C -x 2+2xy-y2,
D x 2+2xy+y2
D例 运用完全平方公式计算:(1)(a+b)2-(a-b)2
(2)(a+b+1)2应用完全平方公式进行数的计算 例:运用完全平方公式计算: 1042 ? ? 解:1042=(100+4)2
=1002+2×100×4+42
=10000+800+16
=10816
运用完全平方公式计算:1982 解 1982=(200-2)2
=2002-2×200×2+22
=40000-800+4
=39204
完全平方公式和平方差公式不同:形式不同:平方差公式是两数和与两数差的积
完全平方公式的两数和的平方结果不同:完全平方公式的结果 是三项,
即 (a ?b)2=a2 ?2ab+b2;平方差公式的结果 是两项,
即 (a+b)(a?b)=a2?b2.(1)化简: (2m+1)2 - (2m)2(3)用简便的方法计算: 23452+0.76552+2.469×0.7655做一做:(4)如果x2+ax+36是一个完全平方式,那么a=______(6)已知(a+b)2=11,ab=1,求(a-b)2的值.做一做:(5)如果x2+6x+b2是一个完全平方式,那么b= ;
