1.3-1三角函数的诱导公式
图片预览








文档简介
课件27张PPT。第一课时1.3 三角函数的诱导公式 湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作一、课前预热利用公式一可以把绝对值较大的角的三角函数转化为 内的角的三角函数值. (大化小) 二、导入新课互动:(抢答)4.利用公式一,可将任意角的三角函数值,转化为00~3600范围内的三角函数值.其中锐角的三角函数可以查表计算,而对于900~3600范围内的三角函数值,能否转化为锐角的三角函数值呢?如果能的话,那么任意角的三角函数求值,都可以化归为锐角三角函数求值,最终得到解决,本节课我们就来讨论这一问题.
思考1:对于任意给定的一个角α,角π+α的终边与角α的终边有什么关系?知识探究(一):π+α的诱导公式
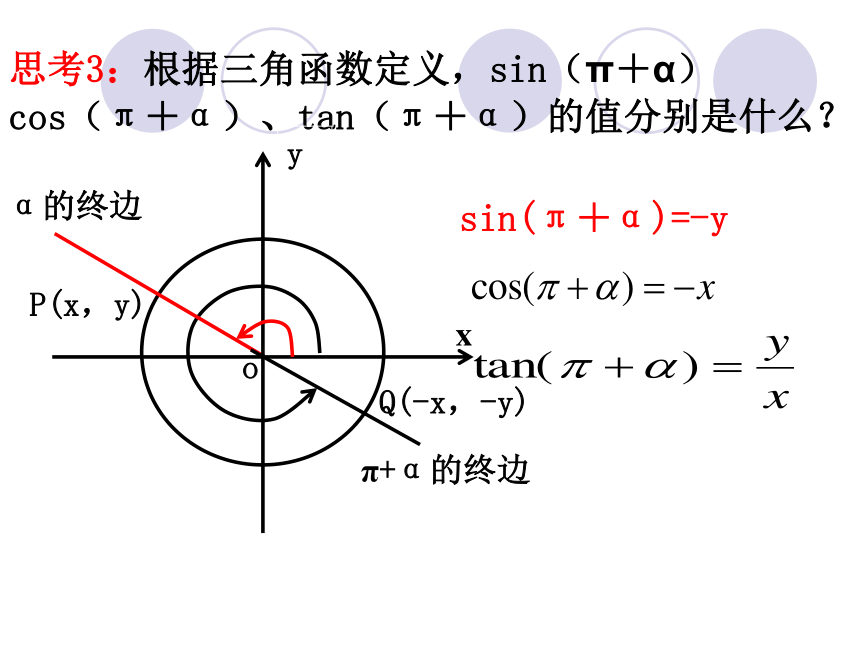
思考2:设角α的终边与单位圆交于点P(x,y),则角π+α的终边与单位圆的交点坐标如何?思考3:根据三角函数定义,sin(π+α) 、cos(π+α)、tan(π+α)的值分别是什么?思考4: 对比sinα,cosα,tanα的值你可以得
到哪些对应关系?思考1:对于任意给定的一个角α,角π+α的终边与角α的终边有什么关系?知识探究(一):π+α的诱导公式
思考2:设角α的终边与单位圆交于点P(x,y),则角π+α的终边与单位圆的交点坐标如何?Q(-x,-y)P(x,y)思考3:根据三角函数定义,sin(π+α)
cos(π+α)、tan(π+α)的值分别是什么?sin(π+α)=-y 对比sinα,cosα,tanα的值有:作用:把第三象限角的三角函数转化为第一象限角的三角函数 公式二: 知识探究(二):-α,π-α的诱导公式: 思考1:对于任意给定的一个角α,-α的终边与α的终边有什么关系? 思考2:设角α的终边与单位圆交于点 P(x,y),则-α的终边与单位圆的交点坐标如何?思考3: 根据三角函数定义,-α的三角函数与α的三角函数有什么关系?思考4: 利用π-α=π+(-α),结合公式二、三,你能得到什么结论?知识探究(二):-α,π-α的诱导公式: 思考二:设角α的终边与单位圆交于点 P(x,y),则-α的终边与单位圆的交点坐标如何?P(x,-y) 公式三: 思考三 根据三角函数定义,-α的三角函数与α的三角函数有什么关系?思考四 利用π-α=π+(-α),结合公式二、三,你能得到什么结论? 公式四: 公式三的作用:把负角的三角函数化为正角的
三角函数
公式四的作用:把第二象限的三角函数化为第一
象限的三角函数
诱导公式的记忆方法
诱导公式一~四可用口诀“函数名不变,符号看象限”记忆,其中“函数名不变”是指等式两边的三角函数同名,“符号”是指等号右边是正号还是负号,“看象限”是指把α看成锐角时原三角函数中角所在的象限.例题分析例1 求下列各三角函数的值: 利用诱导公式把任意角的三角函数转化为锐角三角
函数,一般按下面步骤进行:任意负角的
三角函数任意正角的
三角函数锐角三
角函数 到 的角
的三角函数求值负化正,大化小,化到锐角为终了 例2 化简:
(1) ;
(2) .[分析] 先观察角的特点,选用恰当的诱导公式化简,然后依据同角关系式求解.[答案] -1
[分析] 由于k的奇偶性影响到sin(kπ-α),cos(kπ+α)等的结果,故应对k分奇偶讨论.2.以诱导公式一~四为基础,还可以产生一些派生公式,
如sin(2π-α)=-sinα,
sin(3π-α)=sinα等.小结作业1.诱导公式都是恒等式,即在等式有意义时恒成立.
作业:
P27练习:1,2,3,4.
高中数学老师欧阳文丰制作一、课前预热利用公式一可以把绝对值较大的角的三角函数转化为 内的角的三角函数值. (大化小) 二、导入新课互动:(抢答)4.利用公式一,可将任意角的三角函数值,转化为00~3600范围内的三角函数值.其中锐角的三角函数可以查表计算,而对于900~3600范围内的三角函数值,能否转化为锐角的三角函数值呢?如果能的话,那么任意角的三角函数求值,都可以化归为锐角三角函数求值,最终得到解决,本节课我们就来讨论这一问题.
思考1:对于任意给定的一个角α,角π+α的终边与角α的终边有什么关系?知识探究(一):π+α的诱导公式
思考2:设角α的终边与单位圆交于点P(x,y),则角π+α的终边与单位圆的交点坐标如何?思考3:根据三角函数定义,sin(π+α) 、cos(π+α)、tan(π+α)的值分别是什么?思考4: 对比sinα,cosα,tanα的值你可以得
到哪些对应关系?思考1:对于任意给定的一个角α,角π+α的终边与角α的终边有什么关系?知识探究(一):π+α的诱导公式
思考2:设角α的终边与单位圆交于点P(x,y),则角π+α的终边与单位圆的交点坐标如何?Q(-x,-y)P(x,y)思考3:根据三角函数定义,sin(π+α)
cos(π+α)、tan(π+α)的值分别是什么?sin(π+α)=-y 对比sinα,cosα,tanα的值有:作用:把第三象限角的三角函数转化为第一象限角的三角函数 公式二: 知识探究(二):-α,π-α的诱导公式: 思考1:对于任意给定的一个角α,-α的终边与α的终边有什么关系? 思考2:设角α的终边与单位圆交于点 P(x,y),则-α的终边与单位圆的交点坐标如何?思考3: 根据三角函数定义,-α的三角函数与α的三角函数有什么关系?思考4: 利用π-α=π+(-α),结合公式二、三,你能得到什么结论?知识探究(二):-α,π-α的诱导公式: 思考二:设角α的终边与单位圆交于点 P(x,y),则-α的终边与单位圆的交点坐标如何?P(x,-y) 公式三: 思考三 根据三角函数定义,-α的三角函数与α的三角函数有什么关系?思考四 利用π-α=π+(-α),结合公式二、三,你能得到什么结论? 公式四: 公式三的作用:把负角的三角函数化为正角的
三角函数
公式四的作用:把第二象限的三角函数化为第一
象限的三角函数
诱导公式的记忆方法
诱导公式一~四可用口诀“函数名不变,符号看象限”记忆,其中“函数名不变”是指等式两边的三角函数同名,“符号”是指等号右边是正号还是负号,“看象限”是指把α看成锐角时原三角函数中角所在的象限.例题分析例1 求下列各三角函数的值: 利用诱导公式把任意角的三角函数转化为锐角三角
函数,一般按下面步骤进行:任意负角的
三角函数任意正角的
三角函数锐角三
角函数 到 的角
的三角函数求值负化正,大化小,化到锐角为终了 例2 化简:
(1) ;
(2) .[分析] 先观察角的特点,选用恰当的诱导公式化简,然后依据同角关系式求解.[答案] -1
[分析] 由于k的奇偶性影响到sin(kπ-α),cos(kπ+α)等的结果,故应对k分奇偶讨论.2.以诱导公式一~四为基础,还可以产生一些派生公式,
如sin(2π-α)=-sinα,
sin(3π-α)=sinα等.小结作业1.诱导公式都是恒等式,即在等式有意义时恒成立.
作业:
P27练习:1,2,3,4.
