1.4.1正弦.余弦函数图象
图片预览





文档简介
课件23张PPT。1.4.1正弦.余弦函数图象 湖南省耒阳市振兴学校
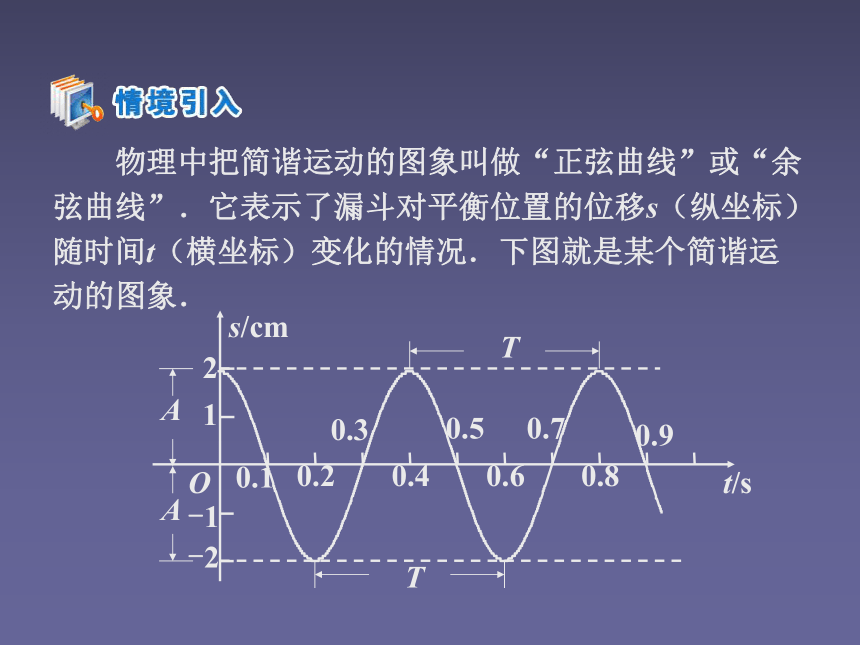
高中数学老师欧阳文丰制作问题与思考1.我们是如何研究一个函数的?函数的定义:y=sinx , y=cosx画函数图像,结合图像观察分析函数的性质。2.画图像的方法:直接法、描点法、图像变化法。简谐运动 物理中把简谐运动的图象叫做“正弦曲线”或“余弦曲线”.它表示了漏斗对平衡位置的位移s(纵坐标)随时间t(横坐标)变化的情况.下图就是某个简谐运动的图象.思考如何用几何方法在直角坐标系中作出点OPMXY.几何描点思考: 能否借助上面作点C的方法,
在直角坐标系中作出正弦函数 的图象呢?讲授新课1. 用单位圆中的正弦线、余弦线作正弦
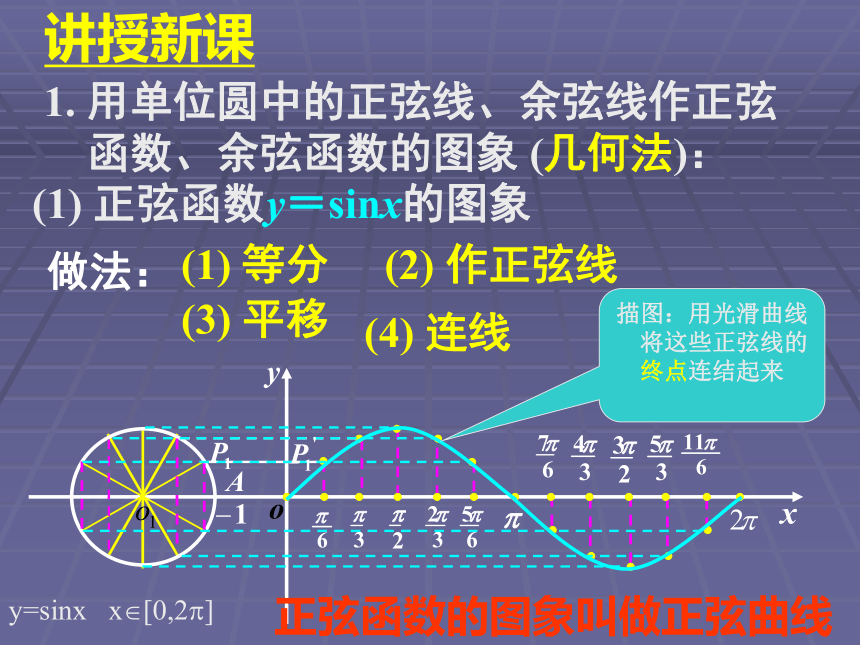
函数、余弦函数的图象 (几何法): (1) 等分(2) 作正弦线(3) 平移(4) 连线做法:(1) 正弦函数y=sinx的图象正弦函数的图象叫做正弦曲线描图:用光滑曲线
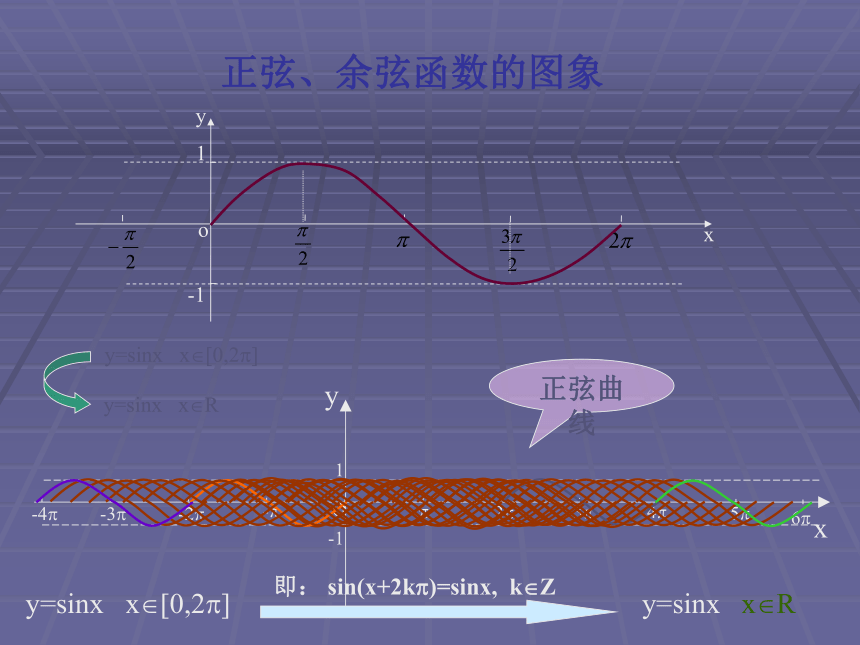
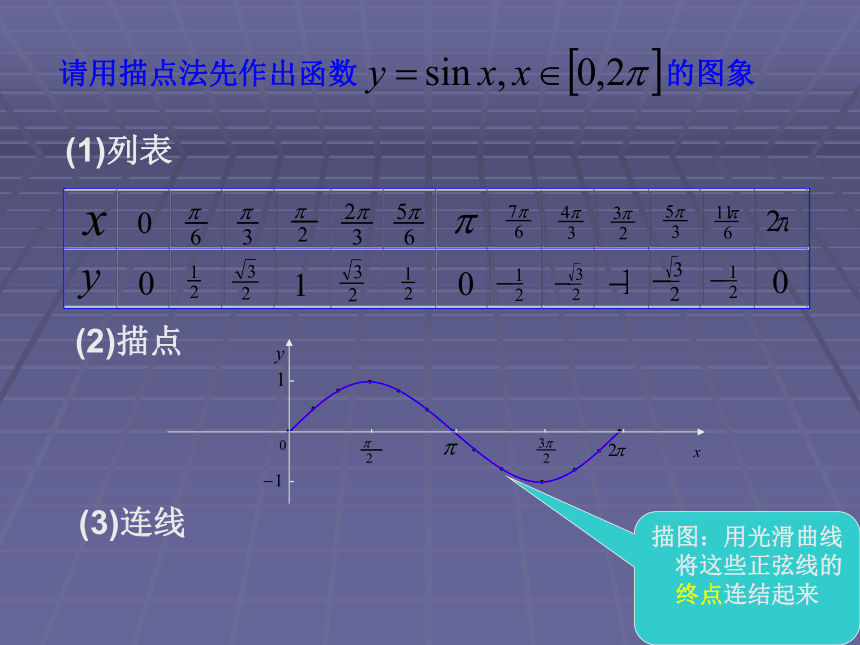
将这些正弦线的终点连结起来y=sinx x?[0,2?] 正弦、余弦函数的图象 正弦曲线y=sinx x?[0,2?] 即: sin(x+2k?)=sinx, k?Zy=sinx x?R(1)列表(2)描点(3)连线请用描点法先作出函数 的图象描图:用光滑曲线
将这些正弦线的终点连结起来 用五点法作正弦函数图象 ①列表(列出对图象形状起关键作用的五点坐标)
②描点(定出五个关键点)
③连线(用光滑的曲线顺次连结五个点)1-1最高点 最低点 与X轴的交点(即函数的零点)01-101 用五点法作y=cosx , x∈[0, 2π]的简图 运用图像变换作余弦函数 y=cosx (x∈R) 的图象思考:如何将余弦函数用诱导公式写成正弦函数? 注:余弦曲线的图象可以通过将正弦曲线向左平移 个单位长度而得到。余弦函数的图象叫做余弦曲线。正弦、余弦曲线例1 画出下列函数的简图:(1)y=1+sinx,x∈[0,2π];(2)y=-cosx,x∈[0,2π].解:(1)按五个关键点列表:101210-1010描点并将它们用光滑的曲线连接起来:y=1+sinx,x∈[0,2π]y=sinx,x∈[0,2π](1)y=1+sinx,x∈[0,2π];(2)y=-cosx,x∈[0,2π].按五个关键点列表:1012-110
-101描点并将它们用光滑的曲线连接起来:(2)y=-cosx,x∈[0,2π].y=-cosx,x∈[0,2π].y=cosx,x∈[0,2π]. 函数值加减,图象上下移动;
自变量加减,图象左右移动.小结函数图像变换: 如何利用y=cos x,x∈[0, 2?]的图
象,通过图形变换(平移、翻转等)来得
到y=2-cosx,x∈[0, 2?]的图象? 先作y=cosx图象关于x轴对称的图形,
得到y=-cosx的图象,再将y=-cosx的
图象向上平移2个单位,得到 y=2-cosx
的图象.小结:探究应用探究应用 不用作图, 你能判断函数
和y=cosx的图象有何关系吗?请在同一坐
标系中画出它们的简图, 以验证你的猜想.小结:这两个函数相等,图象重合. 例2 利用正弦函数和余弦函数的图象,求满足下列条件的x的集合:解:(1)因为y=sinx ,x∈R的函数图象如下:y=sinx ,x∈R 由图可知,当x∈[0,π]、[2π,3π]、[4π,4π]…时,sinx≥0.所以,sinx≥0时,x∈[2kπ,(2k+1)π],k∈Z.因为y=cosx ,x∈R的函数 图象如下:技巧:大于去看顶,小于去找底.1. 正弦曲线、余弦曲线作法3.巩固图象变换的规律:对自变量x“左加右减”,对函数值f(x) “上加下减”.2.注意与诱导公式、三角函数线等知识的联系;课堂小结布置作业:习题1.4 A组1 B组1
在直角坐标系中作出正弦函数 的图象呢?讲授新课1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法): (1) 等分(2) 作正弦线(3) 平移(4) 连线做法:(1) 正弦函数y=sinx的图象正弦函数的图象叫做正弦曲线描图:用光滑曲线
将这些正弦线的终点连结起来y=sinx x?[0,2?] 正弦、余弦函数的图象 正弦曲线y=sinx x?[0,2?] 即: sin(x+2k?)=sinx, k?Zy=sinx x?R(1)列表(2)描点(3)连线请用描点法先作出函数 的图象描图:用光滑曲线
将这些正弦线的终点连结起来 用五点法作正弦函数图象 ①列表(列出对图象形状起关键作用的五点坐标)
②描点(定出五个关键点)
③连线(用光滑的曲线顺次连结五个点)1-1最高点 最低点 与X轴的交点(即函数的零点)01-101 用五点法作y=cosx , x∈[0, 2π]的简图 运用图像变换作余弦函数 y=cosx (x∈R) 的图象思考:如何将余弦函数用诱导公式写成正弦函数? 注:余弦曲线的图象可以通过将正弦曲线向左平移 个单位长度而得到。余弦函数的图象叫做余弦曲线。正弦、余弦曲线例1 画出下列函数的简图:(1)y=1+sinx,x∈[0,2π];(2)y=-cosx,x∈[0,2π].解:(1)按五个关键点列表:101210-1010描点并将它们用光滑的曲线连接起来:y=1+sinx,x∈[0,2π]y=sinx,x∈[0,2π](1)y=1+sinx,x∈[0,2π];(2)y=-cosx,x∈[0,2π].按五个关键点列表:1012-110
-101描点并将它们用光滑的曲线连接起来:(2)y=-cosx,x∈[0,2π].y=-cosx,x∈[0,2π].y=cosx,x∈[0,2π]. 函数值加减,图象上下移动;
自变量加减,图象左右移动.小结函数图像变换: 如何利用y=cos x,x∈[0, 2?]的图
象,通过图形变换(平移、翻转等)来得
到y=2-cosx,x∈[0, 2?]的图象? 先作y=cosx图象关于x轴对称的图形,
得到y=-cosx的图象,再将y=-cosx的
图象向上平移2个单位,得到 y=2-cosx
的图象.小结:探究应用探究应用 不用作图, 你能判断函数
和y=cosx的图象有何关系吗?请在同一坐
标系中画出它们的简图, 以验证你的猜想.小结:这两个函数相等,图象重合. 例2 利用正弦函数和余弦函数的图象,求满足下列条件的x的集合:解:(1)因为y=sinx ,x∈R的函数图象如下:y=sinx ,x∈R 由图可知,当x∈[0,π]、[2π,3π]、[4π,4π]…时,sinx≥0.所以,sinx≥0时,x∈[2kπ,(2k+1)π],k∈Z.因为y=cosx ,x∈R的函数 图象如下:技巧:大于去看顶,小于去找底.1. 正弦曲线、余弦曲线作法3.巩固图象变换的规律:对自变量x“左加右减”,对函数值f(x) “上加下减”.2.注意与诱导公式、三角函数线等知识的联系;课堂小结布置作业:习题1.4 A组1 B组1
