5.1.3 数据的直观表示 导学案(含答案)
文档属性
| 名称 | 5.1.3 数据的直观表示 导学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 449.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 11:17:16 | ||
图片预览


文档简介
5.1.3 数据的直观表示
学习目标
1.能够在图形中读出相关信息,会画频率分布直方图,会用频率分布直方图估计总体.
2.培养学生利用数学方法分析数据、解决实际问题的能力.
3.通过画图培养学生耐心细致,严谨认真的科学态度.
自主预习
1.能够读懂柱状图、折线图及扇形图.
2.会画茎叶图,能通过茎叶图求中位数、众数以及能够比较方差的大小.
3.会画频率分布直方图,能通过频率分布直方图求中位数.
课堂探究
【问题一】2015年7月6日的《中国青年报》报道:根据调查,有担当(76.5%)和踏实(74.5%)的年轻人最被受访者欣赏.奋进(54.7%)、坚毅(54.1%)、有梦想(50.2%),有闯劲(40.1%)、沉稳(36.7%)、直率(34.6%)、幽默(33.4%)、活泼(27.2%)、庄重(20.3%)、洒脱(20.0%)也是受访者欣赏的品质.
你能将这一调查结果用图表进行形象化表示吗 如何使杂乱无章的数字更加直观,让人一目了然受访者更欣赏什么品质
【思考】柱状图的特点是什么 优点是什么
常考题型
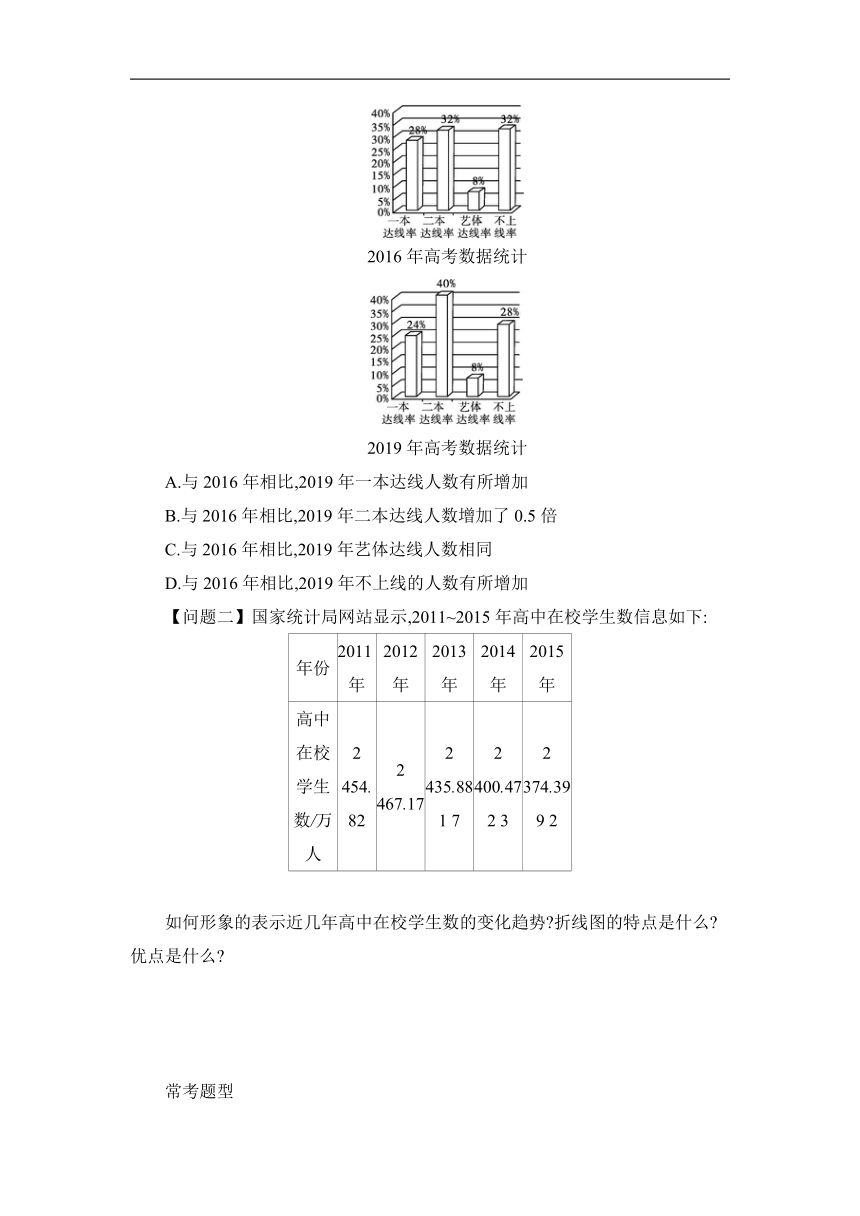
1.某地某所高中2019年的高考考生人数是2016年高考考生人数的1.5倍,为了更好地对比该校考生的升学情况,统计了该校2016年和2019年的高考升学情况,得到如下柱图.
则下列结论正确的是( )
2016年高考数据统计
2019年高考数据统计
A.与2016年相比,2019年一本达线人数有所增加
B.与2016年相比,2019年二本达线人数增加了0.5倍
C.与2016年相比,2019年艺体达线人数相同
D.与2016年相比,2019年不上线的人数有所增加
【问题二】国家统计局网站显示,2011~2015年高中在校学生数信息如下:
年份 2011年 2012年 2013年 2014年 2015年
高中在校 学生数/万人 2 454.82 2 467.17 2 435.881 7 2 400.472 3 2 374.399 2
如何形象的表示近几年高中在校学生数的变化趋势 折线图的特点是什么 优点是什么
常考题型
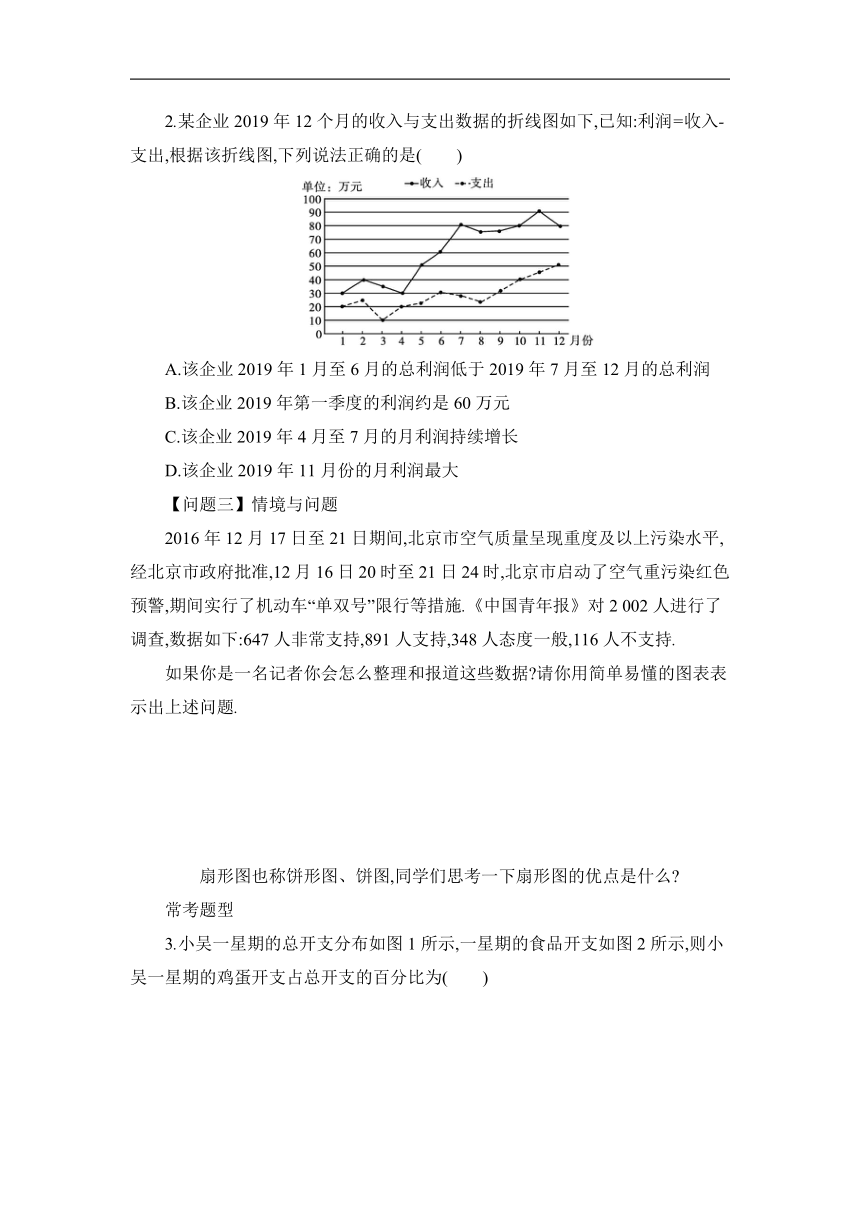
2.某企业2019年12个月的收入与支出数据的折线图如下,已知:利润=收入-支出,根据该折线图,下列说法正确的是( )
A.该企业2019年1月至6月的总利润低于2019年7月至12月的总利润
B.该企业2019年第一季度的利润约是60万元
C.该企业2019年4月至7月的月利润持续增长
D.该企业2019年11月份的月利润最大
【问题三】情境与问题
2016年12月17日至21日期间,北京市空气质量呈现重度及以上污染水平,经北京市政府批准,12月16日20时至21日24时,北京市启动了空气重污染红色预警,期间实行了机动车“单双号”限行等措施.《中国青年报》对2 002人进行了调查,数据如下:647人非常支持,891人支持,348人态度一般,116人不支持.
如果你是一名记者你会怎么整理和报道这些数据 请你用简单易懂的图表表示出上述问题.
扇形图也称饼形图、饼图,同学们思考一下扇形图的优点是什么
常考题型
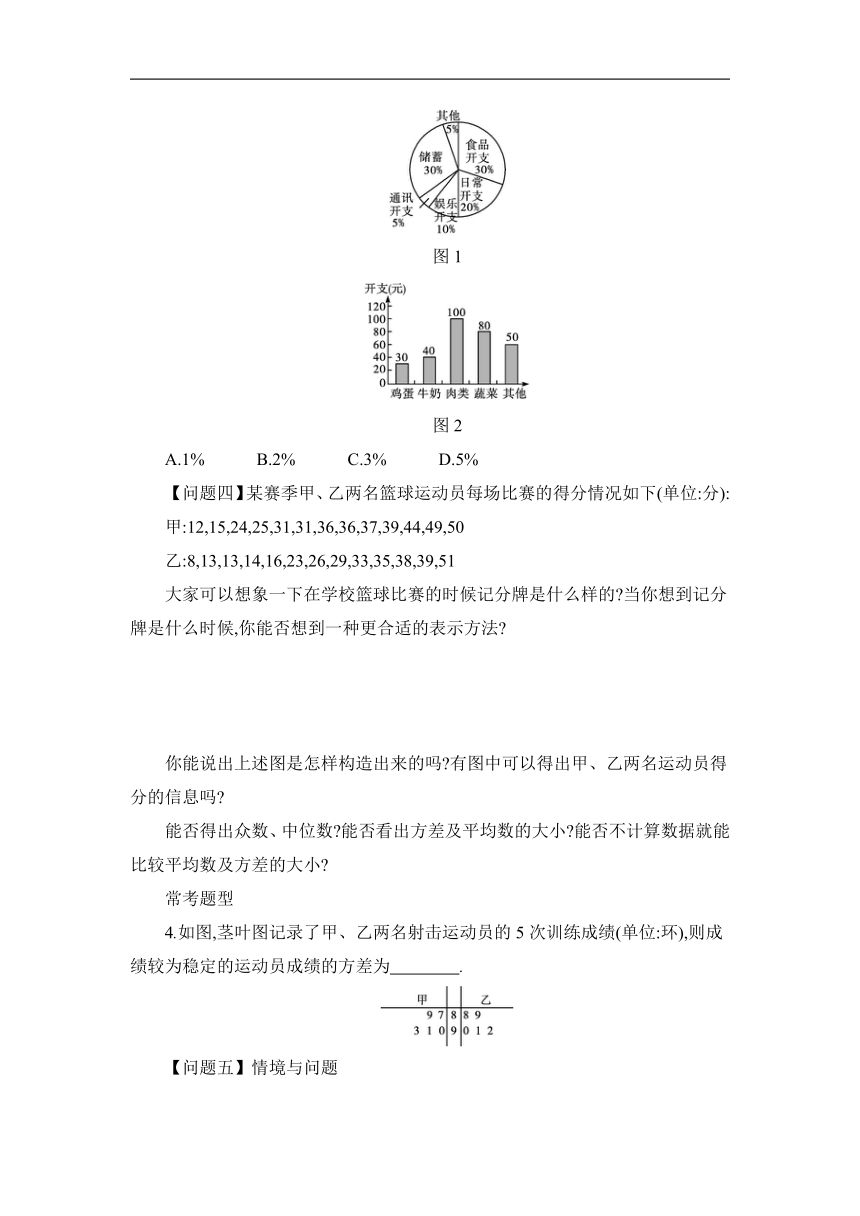
3.小吴一星期的总开支分布如图1所示,一星期的食品开支如图2所示,则小吴一星期的鸡蛋开支占总开支的百分比为( )
图1
图2
A.1% B.2% C.3% D.5%
【问题四】某赛季甲、乙两名篮球运动员每场比赛的得分情况如下(单位:分):
甲:12,15,24,25,31,31,36,36,37,39,44,49,50
乙:8,13,13,14,16,23,26,29,33,35,38,39,51
大家可以想象一下在学校篮球比赛的时候记分牌是什么样的 当你想到记分牌是什么时候,你能否想到一种更合适的表示方法
你能说出上述图是怎样构造出来的吗 有图中可以得出甲、乙两名运动员得分的信息吗
能否得出众数、中位数 能否看出方差及平均数的大小 能否不计算数据就能比较平均数及方差的大小
常考题型
4.如图,茎叶图记录了甲、乙两名射击运动员的5次训练成绩(单位:环),则成绩较为稳定的运动员成绩的方差为 .
【问题五】情境与问题
课本72页是某学校全体学生一次政治考试的成绩(成绩省略,具体数据看课本).
(1)能否直接用前面提到过的图来表示上述数据 为什么
(2)怎样才能直观地表示出上述数据的大致分布情况(比如指出哪个分数段的分数比较多,哪个分数段的分数比较少)
自己总结绘制频率分布直方图的步骤
例题讲解
例1 为了了解学生的课业负担,甲、乙两所学校分别抽200名在校学生,了解他们完成作业所需的时间,并分别作出了频率分布直方图如图(1)(2)所示,其中分组的区间都为[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3],记甲学校所得的中位数为x,乙学校所得的中位数为y,判断x与y的相对大小.
(1)
(2)
例2 某射击远动员一次射击训练的成绩可以整理成如图所示的频率分布直方图,试计算这次成绩的平均数与方差.
常考题型
5.某校高二理科学生期末数学考试成绩的频率分布直方图如图,则本次考试中该校高二理科学生数学成绩的中位数的估计值为 .(精确到0.01)
6.某校为了了解学生每天平均课外阅读的时间(单位:分钟),从本校随机抽取了100名学生进行调查,根据收集的数据,得到学生每天课外阅读时间的频率分布直方图,如图所示,若每天课外阅读时间不超过30分钟的有45人.
(1)求a,b的值;
(2)根据频率分布直方图,估计该校学生每天课外阅读时间的中位数及平均值(同一组中的数据用该组区间的中点值代表).
核心素养专练
1.如图所示的是甲、乙、丙三个企业的产品成本(单位:万元)及其构成比例,则下列判断正确的是( )
A.乙企业支付的工资占成本的比重在三个企业中最大
B.由于丙企业生产规模最大,故它的其他费用占成本的比重也最大
C.甲企业本着勤俭创业的原则,将其他费用降到了最低
D.乙企业用于工资和其他费用的支出额比甲、丙都高
2.空气质量指数AQI是检测空气质量的重要参数,其数值越大说明空气污染状况越严重,空气质量越差.某地环保部门统计了该地区某月1日至24日连续24天的空气质量指数AQI,根据得到的数据绘制出如图所示的折线图,则下列说法错误的是( )
A.该地区在该月2日空气质量最好
B.该地区在该月24日空气质量最差
C.该地区从该月7日到12日AQI持续增大
D.该地区的空气质量指数AQI与这段日期成负相关
3.为全面地了解学生对任课教师教学的满意程度,特在某班开展教学调查.采用简单随机抽样的办法,从该班抽取20名学生,根据他们对语文、数学教师教学的满意度评分(百分制),绘制茎叶图如图.设这20名学生对语文、数学教师教学的满意度评分的中位数分别为a,b,则( )
A.ab
C.a=b D.无法确定
4.某地区100位居民的月用水量(单位:t)的分组及各组的频数如下:[0,0.5),4;[0.5,1),8;[1,1.5),15;[1.5,2),22;[2,2.5),25;[2.5,3),14;[3,3.5),6;[3.5,4),4;[4,4.5],2.
(1)列出样本的频率分布表;
(2)画出频率(或频数)分布直方图,并根据直方图估计这组数据的平均数、中位数、众数;
(3)当地政府制定了人均月用水量为3 t的标准,若超出标准则加倍收费,当地政府解释说,85%以上的居民不超出这个标准,这个解释对吗 为什么
参考答案
自主预习
略
课堂探究
问题一
略
常考题型
1.分析:根据柱状图给出的信息,做差比较即可.
解析:依题意,设2016年高考考生人数为x,则2019年高考考生人数为1.5x.
由24%·1.5x-28%·x=8%·x>0,故选项A正确;
由(40%·1.5x-32%·x)÷32%·x=,故选项B不正确;
由8%·1.5x-8%·x=4%·x>0,故选项C不正确;
由28%·1.5x-32%·x=10%·x>0,故选项D正确.
故选AD.
问题二
略
常考题型
2.分析:由企业2019年12个月的收入与支出数据的折线图直接求解.
解析:由企业2019年12个月的收入与支出数据的折线图,得
在A中,该企业2019年1月至6月的总利润约为
x1=(30+40+35+30+50+60)-(20+25+10+20+22+30)=118.
该企业2019年7月至12月的总利润约为
(80+75+75+80+90+80)-(28+22+30+40+45+50)=265.
∴该企业2019年1月至6月的总利润低于2019年7月至12月的总利润,故A正确;
在B中,该企业2019年第一季度的利润约是
(30+40+35)-(20+25+10)=50(万元),故B错误;
在C中,该企业2019年4月至7月的月利润分别为(单位:万元):10,28,30,52,
∴该企业2019年4月至7月的月利润持续增长,故C正确;
在D中,该企业2019年7月和8月的月利润比11月份的月利润大,故D错误.
故选AC.
问题三
略
常考题型
3.分析:由图1知食品开支占总开支的30%,由图2知鸡蛋开支占食品开支的,由此求得鸡蛋开支占总开支的百分比.
解析:由图1知,食品开支占总开支的30%,
由图2知,鸡蛋开支占食品开支的
=,
∴鸡蛋开支占总开支的百分比为30%×=3%.
故选C.
问题四
略
常考题型
4.分析:根据茎叶图中的数据判断乙的成绩较为稳定,计算乙的平均数和方差即可.
解析:根据茎叶图中的数据知,甲的成绩为87,89,90,91和93;
乙的成绩为88、89、90、91和92,
∴乙的成绩分布均匀些.
乙的平均成绩为=×(88+89+90+91+92)=90,
方差为
s2=[(88-90)2+(89-90)2+(90-90)2+(91-90)2+(92-90)2]=2.
故答案为2.
问题五
略
例题讲解
略
常考题型
5.分析:由频率分布直方图求出数学成绩在[50,110)的频率为0.36,数学成绩在[110,130)的频率为0.48,由此能求出本次考试中该校高二理科学生数学成绩的中位数的估计值.
解析:由频率分布直方图得
数学成绩在[50,110)的频率为(0.001 6+0.008+0.008 4)×20=0.36,
数学成绩在[110,130)的频率为0.024×20=0.48,
∴本次考试中该校高二理科学生数学成绩的中位数的估计值为:
110+×20≈115.83.
故答案为115.83.
6.分析:(1)由频率分布直方图的性质列出方程组,能求出a,b.
(2)由频率分布直方图,能估计该校学生每天课外阅读时间的中位数及平均值.
解:(1)由题意得
解得
(2)课外阅读时间在[0,30)的频率为(0.005+0.01+0.03)×10=0.45,
课外阅读时间在[30,40)的频率为0.025×10=0.25,
∴中位数为30+×10=32(分钟).
平均数为5×0.05+15×0.1+25×0.3+35×0.25+45×0.2+55×0.1=32.5(分钟).
核心素养专练
1.分析:先对图表的数据分析处理,再结合进行简单的合情推理逐一检验即可得解.
解析:三个企业中甲企业工资所占成本的比重最大,故A错误,
虽然丙企业生产规模大,但它的其他费用开支所占成本的比重与乙企业是一样的,故B错;
甲企业其他费用开支最低,故C正确;
甲企业的工资和其他费用开支额为4 000万元,乙企业为5 400万元,丙企业为6 000万元,所以丙企业用于工资和其他费用支出额比甲、乙都高,故D错误.
故选C.
2.分析:由折线图可以观察出结果.
解析:由折线图可知,该月2日指数AQI值最小,因此空气质量最好;
该月24日指数AQI值最大,因此空气质量最差;
该地区从该月7日到12日AQI值是持续增大;
该地区的空气质量指数AQI与这段日期成正相关.
故选D.
3.分析:由茎叶图分别求出该班学生对语文、数学教师教学的满意度评分的中位数,由此能比较a,b.
解析:由茎叶图得a==71.5,b==76,∴a4.分析:(1)由100位居民的人均月用水量(单位:t)的分组及各组的频数能作出频数分布表.
(2)由频率分布表能画出频率分布直方图,由频率分布直方图能求出这组数据的平均数、中位数、众数.
(3)大约有12%的居民月均用水量在3 t以上,88%的居民月均用水量在3 t以下,因此,政府的解释是正确的.
解:(1)作出频数分布表,如下:
分组 频数 频率
[0,0.5) 4 0.04
[0.5,1) 8 0.08
[1,1.5) 15 0.15
[1.5,2) 22 0.22
[2,2.5) 25 0.25
[2.5,3) 14 0.14
[3,3.5) 6 0.06
[3.5,4) 4 0.04
[4,4.5] 2 0.02
合计 100 1.00
(2)由频率分布表画出频率分布直方图,如下:
由频率分布直方图得这组数据的平均数为
=0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.22+2.25×0.25+2.75×0.14+3.25×0.06+3.75×0.04+4.25×0.02=2.02.
∵月用水量在[0,2)的频率为0.04+0.08+0.15+0.22=0.49,
月用水量在[2,2.5)的频率为0.25,
∴中位数为2+×0.5=2.02(t),
众数为=2.25(t).
(3)人均月用水量在3 t以上的居民的比例为6%+4%+2%=12%,
即大约是有12%的居民月均用水量在3 t以上,88%的居民月均用水量在3 t以下,因此,政府的解释是正确的.
学习目标
1.能够在图形中读出相关信息,会画频率分布直方图,会用频率分布直方图估计总体.
2.培养学生利用数学方法分析数据、解决实际问题的能力.
3.通过画图培养学生耐心细致,严谨认真的科学态度.
自主预习
1.能够读懂柱状图、折线图及扇形图.
2.会画茎叶图,能通过茎叶图求中位数、众数以及能够比较方差的大小.
3.会画频率分布直方图,能通过频率分布直方图求中位数.
课堂探究
【问题一】2015年7月6日的《中国青年报》报道:根据调查,有担当(76.5%)和踏实(74.5%)的年轻人最被受访者欣赏.奋进(54.7%)、坚毅(54.1%)、有梦想(50.2%),有闯劲(40.1%)、沉稳(36.7%)、直率(34.6%)、幽默(33.4%)、活泼(27.2%)、庄重(20.3%)、洒脱(20.0%)也是受访者欣赏的品质.
你能将这一调查结果用图表进行形象化表示吗 如何使杂乱无章的数字更加直观,让人一目了然受访者更欣赏什么品质
【思考】柱状图的特点是什么 优点是什么
常考题型
1.某地某所高中2019年的高考考生人数是2016年高考考生人数的1.5倍,为了更好地对比该校考生的升学情况,统计了该校2016年和2019年的高考升学情况,得到如下柱图.
则下列结论正确的是( )
2016年高考数据统计
2019年高考数据统计
A.与2016年相比,2019年一本达线人数有所增加
B.与2016年相比,2019年二本达线人数增加了0.5倍
C.与2016年相比,2019年艺体达线人数相同
D.与2016年相比,2019年不上线的人数有所增加
【问题二】国家统计局网站显示,2011~2015年高中在校学生数信息如下:
年份 2011年 2012年 2013年 2014年 2015年
高中在校 学生数/万人 2 454.82 2 467.17 2 435.881 7 2 400.472 3 2 374.399 2
如何形象的表示近几年高中在校学生数的变化趋势 折线图的特点是什么 优点是什么
常考题型
2.某企业2019年12个月的收入与支出数据的折线图如下,已知:利润=收入-支出,根据该折线图,下列说法正确的是( )
A.该企业2019年1月至6月的总利润低于2019年7月至12月的总利润
B.该企业2019年第一季度的利润约是60万元
C.该企业2019年4月至7月的月利润持续增长
D.该企业2019年11月份的月利润最大
【问题三】情境与问题
2016年12月17日至21日期间,北京市空气质量呈现重度及以上污染水平,经北京市政府批准,12月16日20时至21日24时,北京市启动了空气重污染红色预警,期间实行了机动车“单双号”限行等措施.《中国青年报》对2 002人进行了调查,数据如下:647人非常支持,891人支持,348人态度一般,116人不支持.
如果你是一名记者你会怎么整理和报道这些数据 请你用简单易懂的图表表示出上述问题.
扇形图也称饼形图、饼图,同学们思考一下扇形图的优点是什么
常考题型
3.小吴一星期的总开支分布如图1所示,一星期的食品开支如图2所示,则小吴一星期的鸡蛋开支占总开支的百分比为( )
图1
图2
A.1% B.2% C.3% D.5%
【问题四】某赛季甲、乙两名篮球运动员每场比赛的得分情况如下(单位:分):
甲:12,15,24,25,31,31,36,36,37,39,44,49,50
乙:8,13,13,14,16,23,26,29,33,35,38,39,51
大家可以想象一下在学校篮球比赛的时候记分牌是什么样的 当你想到记分牌是什么时候,你能否想到一种更合适的表示方法
你能说出上述图是怎样构造出来的吗 有图中可以得出甲、乙两名运动员得分的信息吗
能否得出众数、中位数 能否看出方差及平均数的大小 能否不计算数据就能比较平均数及方差的大小
常考题型
4.如图,茎叶图记录了甲、乙两名射击运动员的5次训练成绩(单位:环),则成绩较为稳定的运动员成绩的方差为 .
【问题五】情境与问题
课本72页是某学校全体学生一次政治考试的成绩(成绩省略,具体数据看课本).
(1)能否直接用前面提到过的图来表示上述数据 为什么
(2)怎样才能直观地表示出上述数据的大致分布情况(比如指出哪个分数段的分数比较多,哪个分数段的分数比较少)
自己总结绘制频率分布直方图的步骤
例题讲解
例1 为了了解学生的课业负担,甲、乙两所学校分别抽200名在校学生,了解他们完成作业所需的时间,并分别作出了频率分布直方图如图(1)(2)所示,其中分组的区间都为[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3],记甲学校所得的中位数为x,乙学校所得的中位数为y,判断x与y的相对大小.
(1)
(2)
例2 某射击远动员一次射击训练的成绩可以整理成如图所示的频率分布直方图,试计算这次成绩的平均数与方差.
常考题型
5.某校高二理科学生期末数学考试成绩的频率分布直方图如图,则本次考试中该校高二理科学生数学成绩的中位数的估计值为 .(精确到0.01)
6.某校为了了解学生每天平均课外阅读的时间(单位:分钟),从本校随机抽取了100名学生进行调查,根据收集的数据,得到学生每天课外阅读时间的频率分布直方图,如图所示,若每天课外阅读时间不超过30分钟的有45人.
(1)求a,b的值;
(2)根据频率分布直方图,估计该校学生每天课外阅读时间的中位数及平均值(同一组中的数据用该组区间的中点值代表).
核心素养专练
1.如图所示的是甲、乙、丙三个企业的产品成本(单位:万元)及其构成比例,则下列判断正确的是( )
A.乙企业支付的工资占成本的比重在三个企业中最大
B.由于丙企业生产规模最大,故它的其他费用占成本的比重也最大
C.甲企业本着勤俭创业的原则,将其他费用降到了最低
D.乙企业用于工资和其他费用的支出额比甲、丙都高
2.空气质量指数AQI是检测空气质量的重要参数,其数值越大说明空气污染状况越严重,空气质量越差.某地环保部门统计了该地区某月1日至24日连续24天的空气质量指数AQI,根据得到的数据绘制出如图所示的折线图,则下列说法错误的是( )
A.该地区在该月2日空气质量最好
B.该地区在该月24日空气质量最差
C.该地区从该月7日到12日AQI持续增大
D.该地区的空气质量指数AQI与这段日期成负相关
3.为全面地了解学生对任课教师教学的满意程度,特在某班开展教学调查.采用简单随机抽样的办法,从该班抽取20名学生,根据他们对语文、数学教师教学的满意度评分(百分制),绘制茎叶图如图.设这20名学生对语文、数学教师教学的满意度评分的中位数分别为a,b,则( )
A.ab
C.a=b D.无法确定
4.某地区100位居民的月用水量(单位:t)的分组及各组的频数如下:[0,0.5),4;[0.5,1),8;[1,1.5),15;[1.5,2),22;[2,2.5),25;[2.5,3),14;[3,3.5),6;[3.5,4),4;[4,4.5],2.
(1)列出样本的频率分布表;
(2)画出频率(或频数)分布直方图,并根据直方图估计这组数据的平均数、中位数、众数;
(3)当地政府制定了人均月用水量为3 t的标准,若超出标准则加倍收费,当地政府解释说,85%以上的居民不超出这个标准,这个解释对吗 为什么
参考答案
自主预习
略
课堂探究
问题一
略
常考题型
1.分析:根据柱状图给出的信息,做差比较即可.
解析:依题意,设2016年高考考生人数为x,则2019年高考考生人数为1.5x.
由24%·1.5x-28%·x=8%·x>0,故选项A正确;
由(40%·1.5x-32%·x)÷32%·x=,故选项B不正确;
由8%·1.5x-8%·x=4%·x>0,故选项C不正确;
由28%·1.5x-32%·x=10%·x>0,故选项D正确.
故选AD.
问题二
略
常考题型
2.分析:由企业2019年12个月的收入与支出数据的折线图直接求解.
解析:由企业2019年12个月的收入与支出数据的折线图,得
在A中,该企业2019年1月至6月的总利润约为
x1=(30+40+35+30+50+60)-(20+25+10+20+22+30)=118.
该企业2019年7月至12月的总利润约为
(80+75+75+80+90+80)-(28+22+30+40+45+50)=265.
∴该企业2019年1月至6月的总利润低于2019年7月至12月的总利润,故A正确;
在B中,该企业2019年第一季度的利润约是
(30+40+35)-(20+25+10)=50(万元),故B错误;
在C中,该企业2019年4月至7月的月利润分别为(单位:万元):10,28,30,52,
∴该企业2019年4月至7月的月利润持续增长,故C正确;
在D中,该企业2019年7月和8月的月利润比11月份的月利润大,故D错误.
故选AC.
问题三
略
常考题型
3.分析:由图1知食品开支占总开支的30%,由图2知鸡蛋开支占食品开支的,由此求得鸡蛋开支占总开支的百分比.
解析:由图1知,食品开支占总开支的30%,
由图2知,鸡蛋开支占食品开支的
=,
∴鸡蛋开支占总开支的百分比为30%×=3%.
故选C.
问题四
略
常考题型
4.分析:根据茎叶图中的数据判断乙的成绩较为稳定,计算乙的平均数和方差即可.
解析:根据茎叶图中的数据知,甲的成绩为87,89,90,91和93;
乙的成绩为88、89、90、91和92,
∴乙的成绩分布均匀些.
乙的平均成绩为=×(88+89+90+91+92)=90,
方差为
s2=[(88-90)2+(89-90)2+(90-90)2+(91-90)2+(92-90)2]=2.
故答案为2.
问题五
略
例题讲解
略
常考题型
5.分析:由频率分布直方图求出数学成绩在[50,110)的频率为0.36,数学成绩在[110,130)的频率为0.48,由此能求出本次考试中该校高二理科学生数学成绩的中位数的估计值.
解析:由频率分布直方图得
数学成绩在[50,110)的频率为(0.001 6+0.008+0.008 4)×20=0.36,
数学成绩在[110,130)的频率为0.024×20=0.48,
∴本次考试中该校高二理科学生数学成绩的中位数的估计值为:
110+×20≈115.83.
故答案为115.83.
6.分析:(1)由频率分布直方图的性质列出方程组,能求出a,b.
(2)由频率分布直方图,能估计该校学生每天课外阅读时间的中位数及平均值.
解:(1)由题意得
解得
(2)课外阅读时间在[0,30)的频率为(0.005+0.01+0.03)×10=0.45,
课外阅读时间在[30,40)的频率为0.025×10=0.25,
∴中位数为30+×10=32(分钟).
平均数为5×0.05+15×0.1+25×0.3+35×0.25+45×0.2+55×0.1=32.5(分钟).
核心素养专练
1.分析:先对图表的数据分析处理,再结合进行简单的合情推理逐一检验即可得解.
解析:三个企业中甲企业工资所占成本的比重最大,故A错误,
虽然丙企业生产规模大,但它的其他费用开支所占成本的比重与乙企业是一样的,故B错;
甲企业其他费用开支最低,故C正确;
甲企业的工资和其他费用开支额为4 000万元,乙企业为5 400万元,丙企业为6 000万元,所以丙企业用于工资和其他费用支出额比甲、乙都高,故D错误.
故选C.
2.分析:由折线图可以观察出结果.
解析:由折线图可知,该月2日指数AQI值最小,因此空气质量最好;
该月24日指数AQI值最大,因此空气质量最差;
该地区从该月7日到12日AQI值是持续增大;
该地区的空气质量指数AQI与这段日期成正相关.
故选D.
3.分析:由茎叶图分别求出该班学生对语文、数学教师教学的满意度评分的中位数,由此能比较a,b.
解析:由茎叶图得a==71.5,b==76,∴a
(2)由频率分布表能画出频率分布直方图,由频率分布直方图能求出这组数据的平均数、中位数、众数.
(3)大约有12%的居民月均用水量在3 t以上,88%的居民月均用水量在3 t以下,因此,政府的解释是正确的.
解:(1)作出频数分布表,如下:
分组 频数 频率
[0,0.5) 4 0.04
[0.5,1) 8 0.08
[1,1.5) 15 0.15
[1.5,2) 22 0.22
[2,2.5) 25 0.25
[2.5,3) 14 0.14
[3,3.5) 6 0.06
[3.5,4) 4 0.04
[4,4.5] 2 0.02
合计 100 1.00
(2)由频率分布表画出频率分布直方图,如下:
由频率分布直方图得这组数据的平均数为
=0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.22+2.25×0.25+2.75×0.14+3.25×0.06+3.75×0.04+4.25×0.02=2.02.
∵月用水量在[0,2)的频率为0.04+0.08+0.15+0.22=0.49,
月用水量在[2,2.5)的频率为0.25,
∴中位数为2+×0.5=2.02(t),
众数为=2.25(t).
(3)人均月用水量在3 t以上的居民的比例为6%+4%+2%=12%,
即大约是有12%的居民月均用水量在3 t以上,88%的居民月均用水量在3 t以下,因此,政府的解释是正确的.
