高三物理目标985第2讲课后总结(word版教案)
文档属性
| 名称 | 高三物理目标985第2讲课后总结(word版教案) |
|
|
| 格式 | docx | ||
| 文件大小 | 171.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-27 00:00:00 | ||
图片预览

文档简介
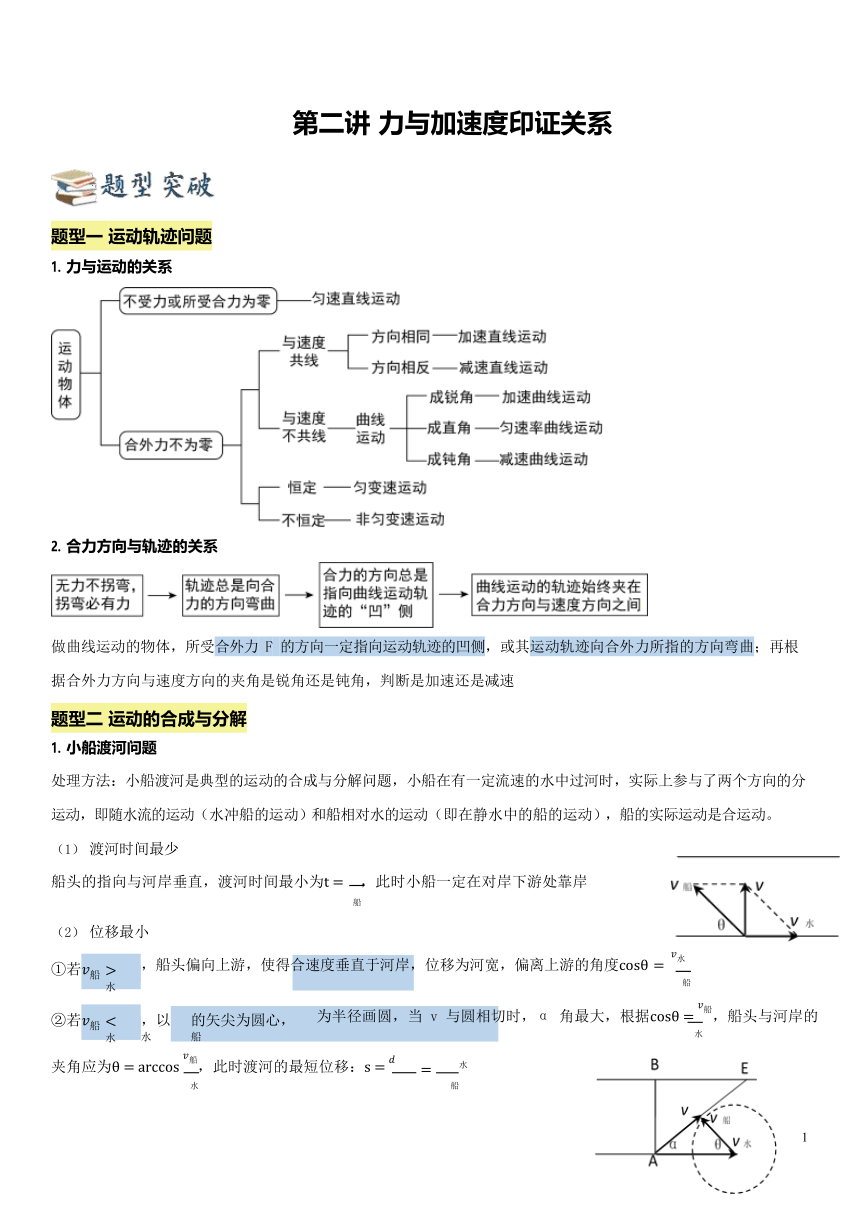
第二讲 力与加速度印证关系
题型一 运动轨迹问题
力与运动的关系
合力方向与轨迹的关系
做曲线运动的物体,所受合外力 F 的方向一定指向运动轨迹的凹侧,或其运动轨迹向合外力所指的方向弯曲;再根据合外力方向与速度方向的夹角是锐角还是钝角,判断是加速还是减速
题型二 运动的合成与分解
小船渡河问题
处理方法:小船渡河是典型的运动的合成与分解问题,小船在有一定流速的水中过河时,实际上参与了两个方向的分运动,即随水流的运动(水冲船的运动)和船相对水的运动(即在静水中的船的运动),船的实际运动是合运动。
渡河时间最少
船头的指向与河岸垂直,渡河时间最小为t = ,此时小船一定在对岸下游处靠岸
船
位移最小
(
1
)
①若 船
> 水
,船头偏向上游,使得合速度垂直于河岸,位移为河宽,偏离上游的角度cosθ = 水
船
②若 船
< 水
,以 水
的矢尖为圆心, 船
为半径画圆,当 v 与圆相切时,α 角最大,根据cosθ = 船,船头与河岸的
水
夹角应为θ = arccos 船,此时渡河的最短位移:s =
水
=
水
船
平抛运动
斜面上的平抛运动
方法 内容 实例 求小球平抛时间 总结
分解速度 水平速度 = 0 竖直速度 = gt 合速度v = √ 2 + 2 特点:tanθ = = 0 如图: = gt ,tanθ = = 0 故 t = 0 分解速度, 构建速度三角形
分解位移 水平位移x = 0 竖直位移y = 1 2 2 合位移 合 = √ 2 + 2 特点:tanθ = = 2 0 如图,x = ,y = 1 2 0 2 而tanθ = , 联立得t = 2 0 分解位移, 构建位移三角形
常见约束条件下平抛时间的确定方法
(
) (
2
)
① =
2 ,这种情况下飞行时间取决于物体下落的高度;
(
√
)
② = 2 0 ,这种情况下飞行时间取决于初速度 v 及斜面倾角;
0
③ = ,这种情况下飞行时间取决于抛点到竖直墙的距离及 v
(
0
)
0
速度关联问题
速度关联问题是指物拉绳(杆)或绳(杆)拉物问题(下面为了方便,统一说“绳”)。解题原则是:把物体的实
际速度分解为垂直于绳和平行于绳的两个分量,根据沿绳方向的分速度大小与绳上各点的速率相同求解。
合速度方向:物体实际运动方向。
分速度方向:①沿绳方向:使绳伸(缩);②垂直于绳方向:使绳转动。
情景 情景一 情景二 情景三 情景四
情景图示
分解图示
定量 结论 = 1 = 0 = 1 = 1 = 1 即 = 1 = 1 即 =
题型三 加速度分解问题
当用正交分解法需要分解的力个数较多,而物体所受的大部分力又在互相垂直的方向上时,通常使尽可能多的力位于两坐标轴上而分解加速度 a,得到 和 ,根据牛顿第二定律得方程组 = , =
(
3
)
题型一 运动轨迹问题
力与运动的关系
合力方向与轨迹的关系
做曲线运动的物体,所受合外力 F 的方向一定指向运动轨迹的凹侧,或其运动轨迹向合外力所指的方向弯曲;再根据合外力方向与速度方向的夹角是锐角还是钝角,判断是加速还是减速
题型二 运动的合成与分解
小船渡河问题
处理方法:小船渡河是典型的运动的合成与分解问题,小船在有一定流速的水中过河时,实际上参与了两个方向的分运动,即随水流的运动(水冲船的运动)和船相对水的运动(即在静水中的船的运动),船的实际运动是合运动。
渡河时间最少
船头的指向与河岸垂直,渡河时间最小为t = ,此时小船一定在对岸下游处靠岸
船
位移最小
(
1
)
①若 船
> 水
,船头偏向上游,使得合速度垂直于河岸,位移为河宽,偏离上游的角度cosθ = 水
船
②若 船
< 水
,以 水
的矢尖为圆心, 船
为半径画圆,当 v 与圆相切时,α 角最大,根据cosθ = 船,船头与河岸的
水
夹角应为θ = arccos 船,此时渡河的最短位移:s =
水
=
水
船
平抛运动
斜面上的平抛运动
方法 内容 实例 求小球平抛时间 总结
分解速度 水平速度 = 0 竖直速度 = gt 合速度v = √ 2 + 2 特点:tanθ = = 0 如图: = gt ,tanθ = = 0 故 t = 0 分解速度, 构建速度三角形
分解位移 水平位移x = 0 竖直位移y = 1 2 2 合位移 合 = √ 2 + 2 特点:tanθ = = 2 0 如图,x = ,y = 1 2 0 2 而tanθ = , 联立得t = 2 0 分解位移, 构建位移三角形
常见约束条件下平抛时间的确定方法
(
) (
2
)
① =
2 ,这种情况下飞行时间取决于物体下落的高度;
(
√
)
② = 2 0 ,这种情况下飞行时间取决于初速度 v 及斜面倾角;
0
③ = ,这种情况下飞行时间取决于抛点到竖直墙的距离及 v
(
0
)
0
速度关联问题
速度关联问题是指物拉绳(杆)或绳(杆)拉物问题(下面为了方便,统一说“绳”)。解题原则是:把物体的实
际速度分解为垂直于绳和平行于绳的两个分量,根据沿绳方向的分速度大小与绳上各点的速率相同求解。
合速度方向:物体实际运动方向。
分速度方向:①沿绳方向:使绳伸(缩);②垂直于绳方向:使绳转动。
情景 情景一 情景二 情景三 情景四
情景图示
分解图示
定量 结论 = 1 = 0 = 1 = 1 = 1 即 = 1 = 1 即 =
题型三 加速度分解问题
当用正交分解法需要分解的力个数较多,而物体所受的大部分力又在互相垂直的方向上时,通常使尽可能多的力位于两坐标轴上而分解加速度 a,得到 和 ,根据牛顿第二定律得方程组 = , =
(
3
)
同课章节目录
