3.1.1椭圆的第二定义 课件(共35张PPT)
文档属性
| 名称 | 3.1.1椭圆的第二定义 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 15:09:38 | ||
图片预览









文档简介
(共35张PPT)
椭圆的第二定义
复习回顾
复习回顾
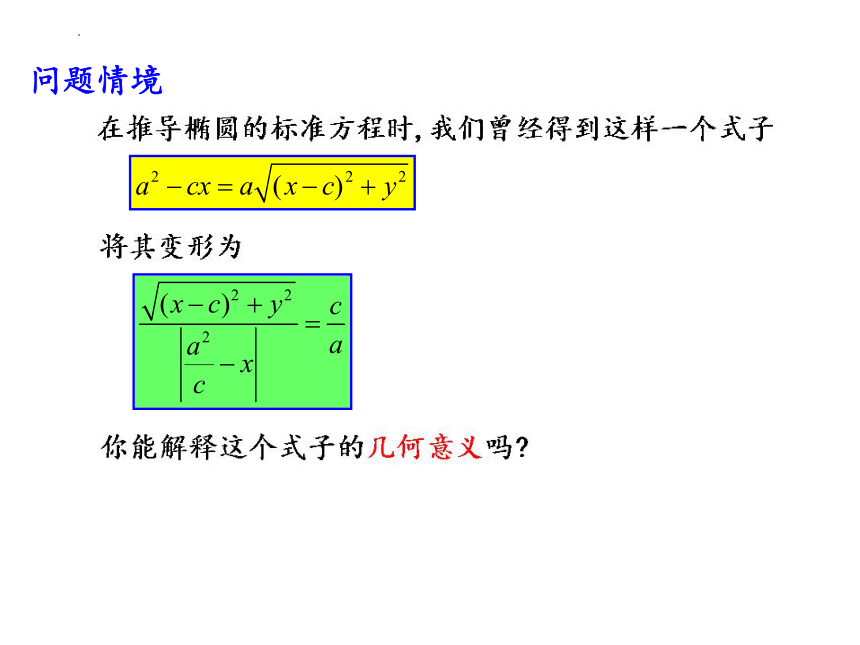
问题情境
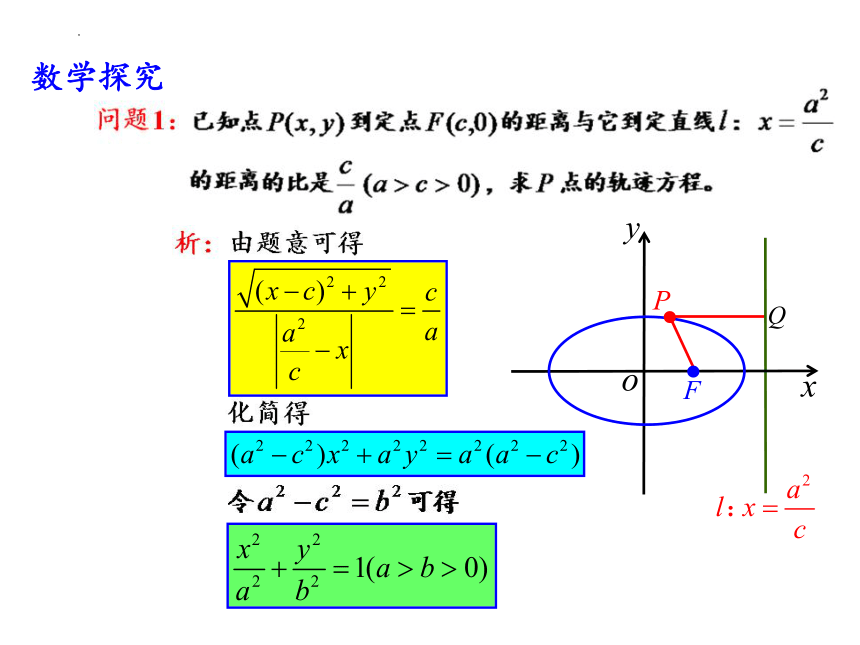
数学探究
数学探究
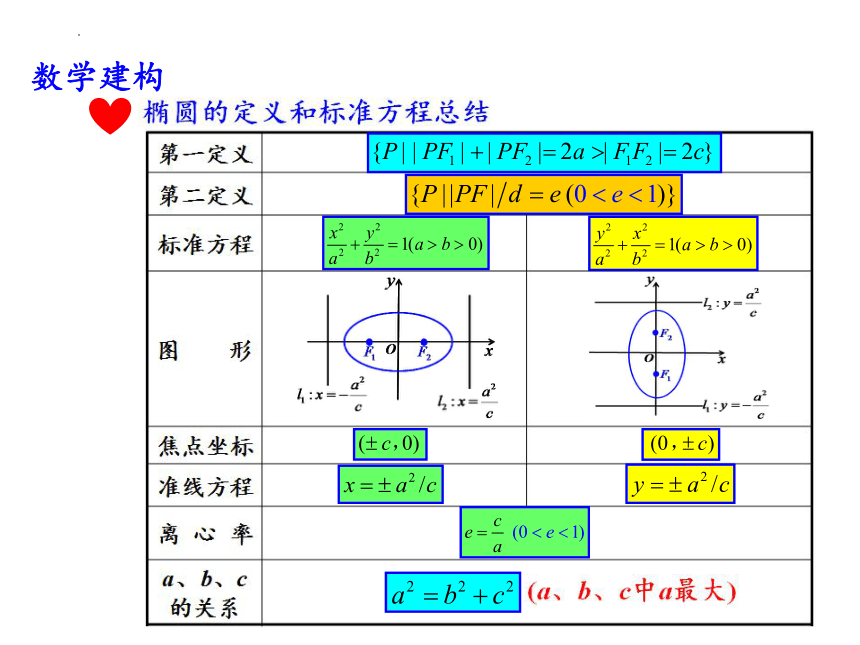
数学建构
数学建构
数学建构
活动探究
类型一 对椭圆第二定义的认识
例1、(1)已知动点P到点(1,0)的距离与它到直线x=4距离之比为0.5,求动点P的轨迹方程。
活动探究
类型一 对椭圆第二定义的认识
例1、(2)已知动点P到直线x=6距离与它到点(2,1)的距离之比为2,求动点P的轨迹方程。
1、中心在坐标原点,准线方程为y=±4,离心率为0.5的椭圆的标准方程为____________
数学练习
2、(1)椭圆x2+2y2=4的焦点坐标为________,准线方程为__________
(2)椭圆4x2+2y2=1的焦点坐标为________,准线方程为__________
数学练习
数学建构
2、
数学建构
3、
数学探究
数学探究
数学探究
数学探究
数学建构
4、
当椭圆上的点位于长轴端点时张角最小(等于0o) ,此时张角的余弦值最大(等于1)。
数学建构
5、
活动探究
类型二 椭圆的焦半径与焦点弦问题
例2、
d1
d2
数学练习
1、已知椭圆x2+2y2=4 上一点P到左焦点的距离为3,则点P到右准线的距离为________
数学练习
法一:
方法基础,但计算量太大,考验耐心。
数学练习
法二:画图分析,结合焦半径公式求解
活动探究
类型三 椭圆第二定义的应用
例3、
活动探究
类型三 椭圆第二定义的应用
例3、
思考:条件不变,求|PA|+|PF|的最小值。
课堂检测
1、已知椭圆的短轴长是2,长轴长是短轴长的2倍,则椭圆的中心到准线的距离为________
课堂检测
2、
此处利用两点间距离公式
课堂小结
课堂小结
2、
课堂小结
3、
课堂小结
4、
课堂小结
当椭圆上的点位于长轴端点时张角最小(等于0o) ,此时张角的余弦值最大(等于1)。
5、
课堂小结
椭圆的第二定义
复习回顾
复习回顾
问题情境
数学探究
数学探究
数学建构
数学建构
数学建构
活动探究
类型一 对椭圆第二定义的认识
例1、(1)已知动点P到点(1,0)的距离与它到直线x=4距离之比为0.5,求动点P的轨迹方程。
活动探究
类型一 对椭圆第二定义的认识
例1、(2)已知动点P到直线x=6距离与它到点(2,1)的距离之比为2,求动点P的轨迹方程。
1、中心在坐标原点,准线方程为y=±4,离心率为0.5的椭圆的标准方程为____________
数学练习
2、(1)椭圆x2+2y2=4的焦点坐标为________,准线方程为__________
(2)椭圆4x2+2y2=1的焦点坐标为________,准线方程为__________
数学练习
数学建构
2、
数学建构
3、
数学探究
数学探究
数学探究
数学探究
数学建构
4、
当椭圆上的点位于长轴端点时张角最小(等于0o) ,此时张角的余弦值最大(等于1)。
数学建构
5、
活动探究
类型二 椭圆的焦半径与焦点弦问题
例2、
d1
d2
数学练习
1、已知椭圆x2+2y2=4 上一点P到左焦点的距离为3,则点P到右准线的距离为________
数学练习
法一:
方法基础,但计算量太大,考验耐心。
数学练习
法二:画图分析,结合焦半径公式求解
活动探究
类型三 椭圆第二定义的应用
例3、
活动探究
类型三 椭圆第二定义的应用
例3、
思考:条件不变,求|PA|+|PF|的最小值。
课堂检测
1、已知椭圆的短轴长是2,长轴长是短轴长的2倍,则椭圆的中心到准线的距离为________
课堂检测
2、
此处利用两点间距离公式
课堂小结
课堂小结
2、
课堂小结
3、
课堂小结
4、
课堂小结
当椭圆上的点位于长轴端点时张角最小(等于0o) ,此时张角的余弦值最大(等于1)。
5、
课堂小结
