3.1.1椭圆的定义和标准方程(2)课件-2021-2022学年高二上学期数学苏教版(2019)选择性必修第一册(共43张PPT)
文档属性
| 名称 | 3.1.1椭圆的定义和标准方程(2)课件-2021-2022学年高二上学期数学苏教版(2019)选择性必修第一册(共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 17:57:16 | ||
图片预览











文档简介
(共43张PPT)
椭圆的定义和标准方程(2)
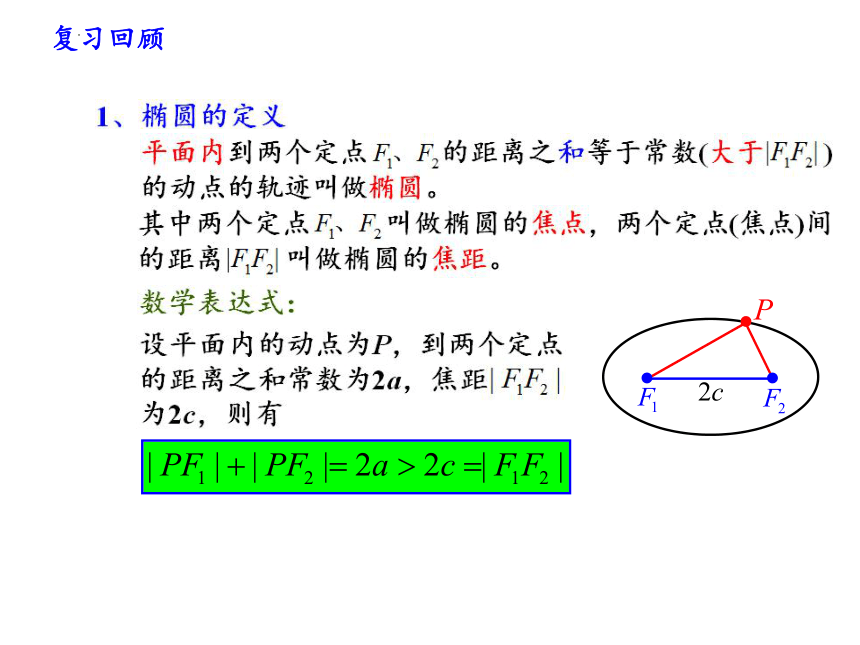
复习回顾
复习回顾
复习回顾
4、求椭圆的标准方程的常用方法和一般步骤
(1)常用方法
(2)一般步骤
复习回顾
5、共焦点的椭圆的标准方程的设法
复习回顾
问题诊断
1、平面内到两个定点F1(0,-4),F2(0,4)的距离之和等于8的动点的轨迹为____________
线段F1F2
问题诊断
2、椭圆9x2+4y2=1的焦点坐标为_______,焦距为_____
问题诊断
3、椭圆2kx2+ky2=1的一个焦点是(0,-4),则k的值为_______
问题诊断
数学建构
(1)常用方法: 、 和 等;
(2)对定义法求轨迹方程的认识
如果能确定动点运动的轨迹满足某种已知曲线的定义,则可以利用这种已知曲线的定义直接写出其方程,这种求轨迹方程的方法称为定义法,定义法在圆锥曲线的问题中被广泛使用,是一种重要的解题方法。
(3)对代入法(相关点法)求轨迹方程的认识
若所求轨迹上的动点P(x,y)与另一个已知曲线C:F(x,y)=0上的动点Q(x1,y1)存在某种联系,可以把点Q的坐标用点P的坐标表示出来,然后代入已知曲线C的方程F(x,y)=0,化简即得所求轨迹方程,这种求轨迹方程的方法叫做代入法(又称为相关点法)。
1、求与椭圆有关的轨迹方程的常用方法及注意点
直接法
定义法
代入法
数学建构
2、椭圆中焦点三角形的面积公式
活动探究
类型一 定义法求椭圆的标准方程
例1、求经过点A(2,0)且与圆(x+2)2+y2=36内切的动圆的圆心M的轨迹方程。
活动探究
类型一 定义法求椭圆的标准方程
例1、求经过点A(2,0)且与圆(x+2)2+y2=36内切的动圆的圆心M的轨迹方程。
数学练习
已知动圆M和圆C1:(x+1)2+y2=36内切,并且和圆C2:(x-1)2+y2=4外切,求动圆圆心M的轨迹方程。
数学练习
已知动圆M和圆C1:(x+1)2+y2=36内切,并且和圆C2:(x-1)2+y2=4外切,求动圆圆心M的轨迹方程。
变式拓展
变式拓展
变式拓展
变式拓展
活动探究
类型一 定义法求椭圆的标准方程
例2、已知B、C是两个定点,|BC|=6,且△ABC的周长等于16,求顶点A的轨迹方程。
活动探究
类型一 定义法求椭圆的标准方程
例2、已知B、C是两个定点,|BC|=6,且△ABC的周长等于16,求顶点A的轨迹方程。
变式拓展
正弦定理
例3、将圆x2+y2=4上各点的横坐标保持不变,纵坐标变为原来的一半,求所得曲线的方程,并说明它是什 么曲线。
活动探究
类型二 代入法(相关点法)求椭圆的标准方程
变式拓展
数学练习
例4、
活动探究
类型三 利用椭圆的标准方程求解参数问题
k∈(0,1)
例4、
活动探究
类型三 利用椭圆的标准方程求解参数问题
思考:(1)上述方程若表示焦点在y轴上的椭圆,求k的取值范围;
k∈(-1,0)
例4、
活动探究
类型三 利用椭圆的标准方程求解参数问题
思考:(2)上述方程若表示椭圆,求k的取值范围;
k∈(-1,0)∪(0,1)
例4、
活动探究
类型三 利用椭圆的标准方程求解参数问题
思考:(3)上述方程若表示圆,求k的取值范围。
解:原方程可化为:(1-k)x2+(1+k)y2-(1-k)(1+k)=0
解得:k=0
∴k的取值范围为{0}
数学练习
数学练习
数学练习
3、若方程4x2+ky2=4 表示的曲线是焦点在y轴上的椭圆,则实数k的取值范围为____________
变式拓展
活动探究
类型四 椭圆中的焦点三角形面积问题
活动探究
类型四 椭圆中的焦点三角形面积问题
数学练习
课堂检测
课堂检测
课堂检测
3、若一椭圆的两个焦点的坐标分别为椭圆9x2+4y2=36的两焦点,并且经过点(2,-3),则该椭圆的标准方程为____________
课堂检测
4、在直角坐标系xOy中,动点P到两点(0,-1)和(0,1)的距离之和等于4,则动点P的轨迹方程为____________
大于2
点P的轨迹是以点(0,-1)和(0,1)为焦点的椭圆,∴2c=2,2a=4
(1)常用方法: 、 和 等;
(2)对定义法求轨迹方程的认识
如果能确定动点运动的轨迹满足某种已知曲线的定义,则可以利用这种已知曲线的定义直接写出其方程,这种求轨迹方程的方法称为定义法,定义法在圆锥曲线的问题中被广泛使用,是一种重要的解题方法。
(3)对代入法(相关点法)求轨迹方程的认识
若所求轨迹上的动点P(x,y)与另一个已知曲线C:F(x,y)=0上的动点Q(x1,y1)存在某种联系,可以把点Q的坐标用点P的坐标表示出来,然后代入已知曲线C的方程F(x,y)=0,化简即得所求轨迹方程,这种求轨迹方程的方法叫做代入法(又称为相关点法)。
1、求与椭圆有关的轨迹方程的常用方法及注意点
直接法
定义法
代入法
课堂小结
2、椭圆中焦点三角形的面积公式
课堂小结
椭圆的定义和标准方程(2)
复习回顾
复习回顾
复习回顾
4、求椭圆的标准方程的常用方法和一般步骤
(1)常用方法
(2)一般步骤
复习回顾
5、共焦点的椭圆的标准方程的设法
复习回顾
问题诊断
1、平面内到两个定点F1(0,-4),F2(0,4)的距离之和等于8的动点的轨迹为____________
线段F1F2
问题诊断
2、椭圆9x2+4y2=1的焦点坐标为_______,焦距为_____
问题诊断
3、椭圆2kx2+ky2=1的一个焦点是(0,-4),则k的值为_______
问题诊断
数学建构
(1)常用方法: 、 和 等;
(2)对定义法求轨迹方程的认识
如果能确定动点运动的轨迹满足某种已知曲线的定义,则可以利用这种已知曲线的定义直接写出其方程,这种求轨迹方程的方法称为定义法,定义法在圆锥曲线的问题中被广泛使用,是一种重要的解题方法。
(3)对代入法(相关点法)求轨迹方程的认识
若所求轨迹上的动点P(x,y)与另一个已知曲线C:F(x,y)=0上的动点Q(x1,y1)存在某种联系,可以把点Q的坐标用点P的坐标表示出来,然后代入已知曲线C的方程F(x,y)=0,化简即得所求轨迹方程,这种求轨迹方程的方法叫做代入法(又称为相关点法)。
1、求与椭圆有关的轨迹方程的常用方法及注意点
直接法
定义法
代入法
数学建构
2、椭圆中焦点三角形的面积公式
活动探究
类型一 定义法求椭圆的标准方程
例1、求经过点A(2,0)且与圆(x+2)2+y2=36内切的动圆的圆心M的轨迹方程。
活动探究
类型一 定义法求椭圆的标准方程
例1、求经过点A(2,0)且与圆(x+2)2+y2=36内切的动圆的圆心M的轨迹方程。
数学练习
已知动圆M和圆C1:(x+1)2+y2=36内切,并且和圆C2:(x-1)2+y2=4外切,求动圆圆心M的轨迹方程。
数学练习
已知动圆M和圆C1:(x+1)2+y2=36内切,并且和圆C2:(x-1)2+y2=4外切,求动圆圆心M的轨迹方程。
变式拓展
变式拓展
变式拓展
变式拓展
活动探究
类型一 定义法求椭圆的标准方程
例2、已知B、C是两个定点,|BC|=6,且△ABC的周长等于16,求顶点A的轨迹方程。
活动探究
类型一 定义法求椭圆的标准方程
例2、已知B、C是两个定点,|BC|=6,且△ABC的周长等于16,求顶点A的轨迹方程。
变式拓展
正弦定理
例3、将圆x2+y2=4上各点的横坐标保持不变,纵坐标变为原来的一半,求所得曲线的方程,并说明它是什 么曲线。
活动探究
类型二 代入法(相关点法)求椭圆的标准方程
变式拓展
数学练习
例4、
活动探究
类型三 利用椭圆的标准方程求解参数问题
k∈(0,1)
例4、
活动探究
类型三 利用椭圆的标准方程求解参数问题
思考:(1)上述方程若表示焦点在y轴上的椭圆,求k的取值范围;
k∈(-1,0)
例4、
活动探究
类型三 利用椭圆的标准方程求解参数问题
思考:(2)上述方程若表示椭圆,求k的取值范围;
k∈(-1,0)∪(0,1)
例4、
活动探究
类型三 利用椭圆的标准方程求解参数问题
思考:(3)上述方程若表示圆,求k的取值范围。
解:原方程可化为:(1-k)x2+(1+k)y2-(1-k)(1+k)=0
解得:k=0
∴k的取值范围为{0}
数学练习
数学练习
数学练习
3、若方程4x2+ky2=4 表示的曲线是焦点在y轴上的椭圆,则实数k的取值范围为____________
变式拓展
活动探究
类型四 椭圆中的焦点三角形面积问题
活动探究
类型四 椭圆中的焦点三角形面积问题
数学练习
课堂检测
课堂检测
课堂检测
3、若一椭圆的两个焦点的坐标分别为椭圆9x2+4y2=36的两焦点,并且经过点(2,-3),则该椭圆的标准方程为____________
课堂检测
4、在直角坐标系xOy中,动点P到两点(0,-1)和(0,1)的距离之和等于4,则动点P的轨迹方程为____________
大于2
点P的轨迹是以点(0,-1)和(0,1)为焦点的椭圆,∴2c=2,2a=4
(1)常用方法: 、 和 等;
(2)对定义法求轨迹方程的认识
如果能确定动点运动的轨迹满足某种已知曲线的定义,则可以利用这种已知曲线的定义直接写出其方程,这种求轨迹方程的方法称为定义法,定义法在圆锥曲线的问题中被广泛使用,是一种重要的解题方法。
(3)对代入法(相关点法)求轨迹方程的认识
若所求轨迹上的动点P(x,y)与另一个已知曲线C:F(x,y)=0上的动点Q(x1,y1)存在某种联系,可以把点Q的坐标用点P的坐标表示出来,然后代入已知曲线C的方程F(x,y)=0,化简即得所求轨迹方程,这种求轨迹方程的方法叫做代入法(又称为相关点法)。
1、求与椭圆有关的轨迹方程的常用方法及注意点
直接法
定义法
代入法
课堂小结
2、椭圆中焦点三角形的面积公式
课堂小结
