3.1.2椭圆的几何性质(1)课件-2021-2022学年高二上学期数学苏教版(2019)选择性必修第一册(共36张PPT)
文档属性
| 名称 | 3.1.2椭圆的几何性质(1)课件-2021-2022学年高二上学期数学苏教版(2019)选择性必修第一册(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 17:57:49 | ||
图片预览






文档简介
(共36张PPT)
椭圆简单的几何性质(1)
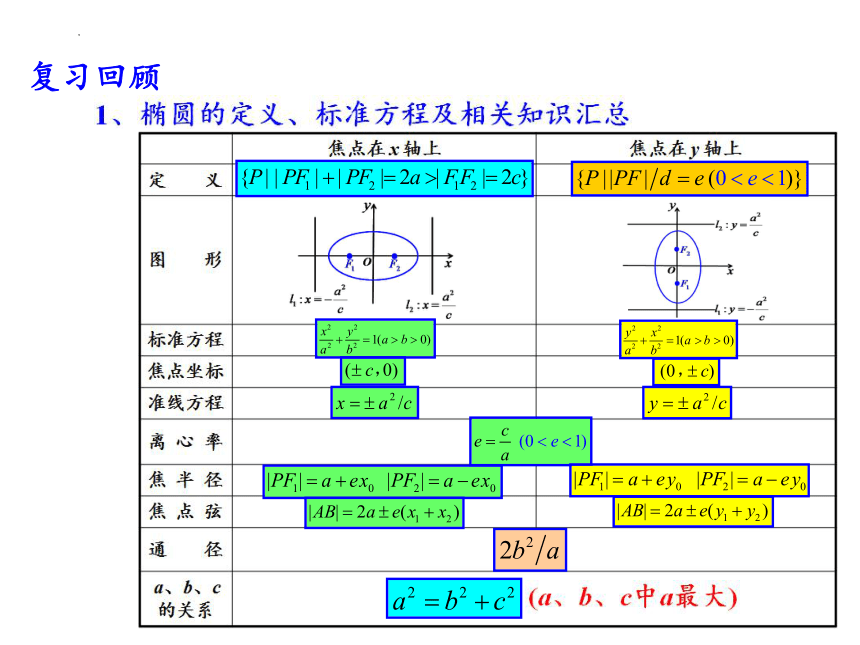
复习回顾
复习回顾
问题情境
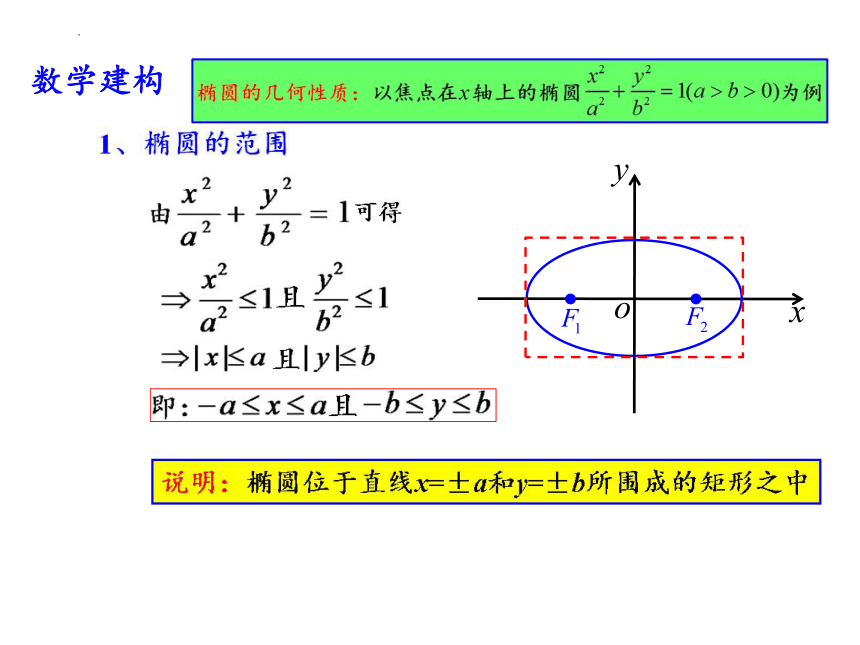
问题:观察椭圆 的形状,
(1)你能从图中看出椭圆上任意一点(x,y)的横坐标x和 纵坐标y的取值范围吗?
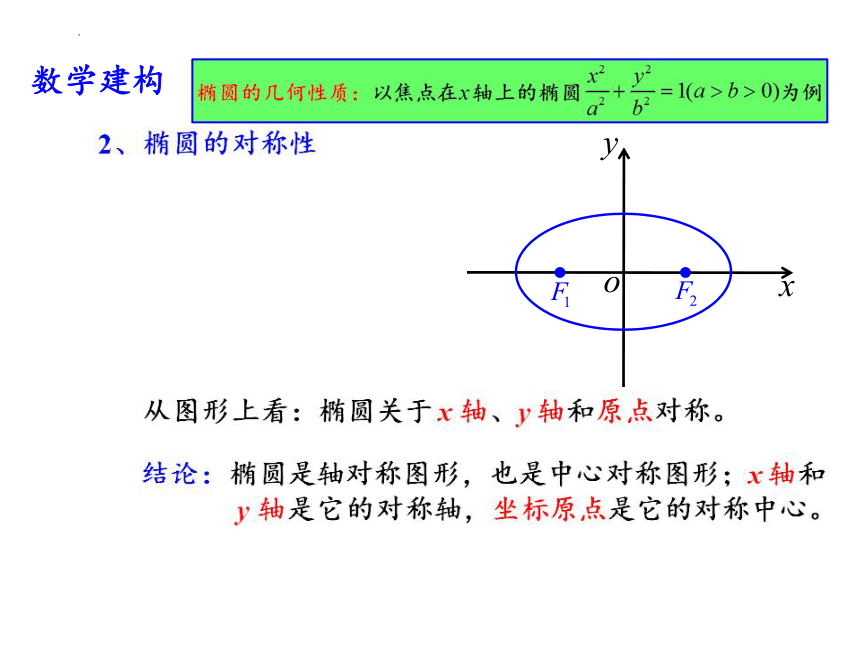
(2)椭圆具有怎样的对称性?
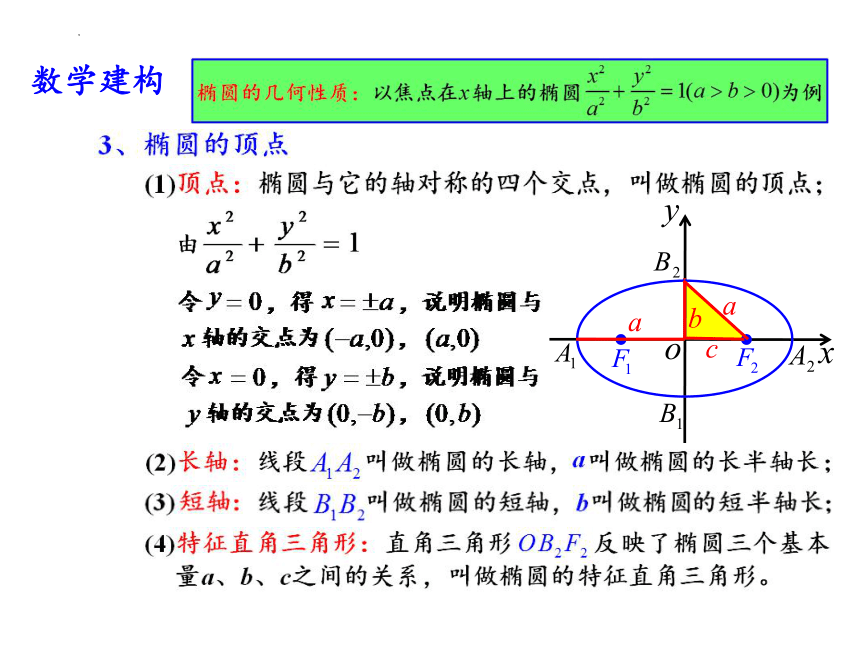
(3)椭圆上有哪些特殊点?
(4)椭圆还有哪些其它的几何性质?
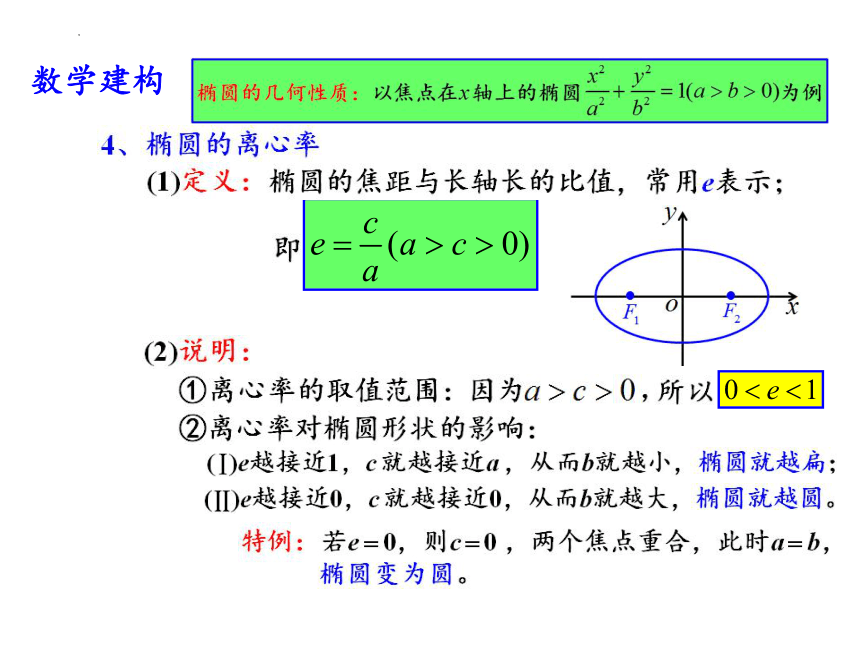
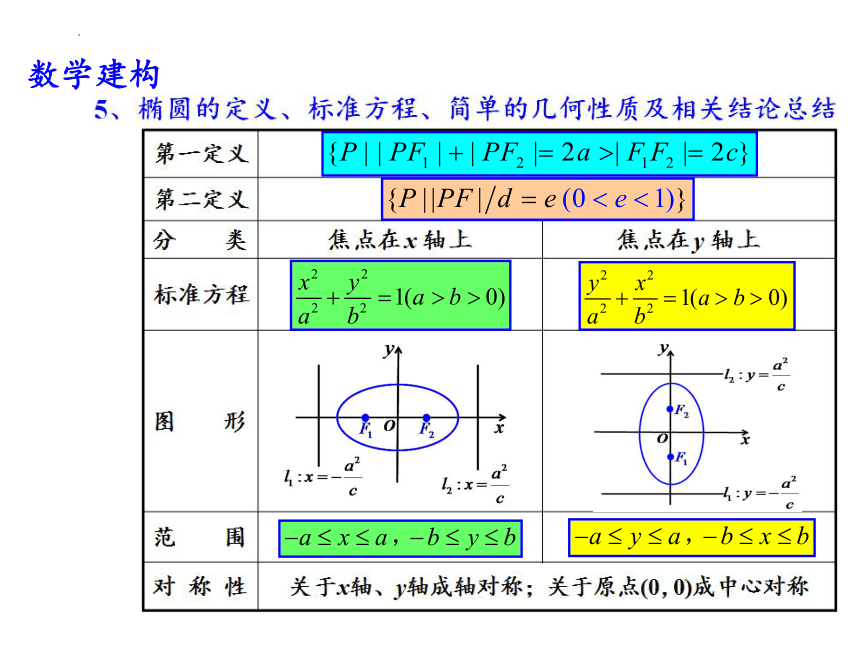
数学建构
数学建构
数学建构
数学建构
数学建构
数学建构
数学建构
数学建构
活动探究
类型一 对椭圆的几何性质的认识
-5≤x≤5且-3≤y≤3
10
6
8
(±4,0)
(±5,0)(0,±3)
(±5,0)
x轴和y轴
(0,0)
数学练习
1、已知椭圆25x2+16y2=400,则它的范围为_________, 长轴长为_____,短轴长为_____,焦距为____,焦点坐标为_____,顶点坐标为__ _____,对称轴为_____,对称中心为____,离心率为______
2、已知椭圆4x2+3y2=12,则它的范围为____________,长轴长为____,短轴长为_____,焦距为____,焦点坐标为_____,顶点坐标为___ ____,对称轴为_____,对称中心为____,离心率为______
-4≤x≤4且-5≤y≤5
10
8
6
(0,±3)
(±4,0)(0,±5)
x轴和y轴
(0,0)
8
2
(0,±1)
x轴和y轴
(0,0)
活动探究
类型二 利用椭圆的几何性质求椭圆的标准方程
例2、根据下列条件分别求椭圆的标准方程。
活动探究
类型二 利用椭圆的几何性质求椭圆的标准方程
(2)长轴长是短轴长的3倍,且经过点(0,3);
例2、根据下列条件分别求椭圆的标准方程。
活动探究
类型二 利用椭圆的几何性质求椭圆的标准方程
(3)焦距是8,离心率为0.8;
例2、根据下列条件分别求椭圆的标准方程。
解:
活动探究
类型二 利用椭圆的几何性质求椭圆的标准方程
例2、根据下列条件分别求椭圆的标准方程。
活动探究
类型三 椭圆几何性质的实际应用
例4、我国发射的第一颗人造地球卫星的运行轨道是以地球的中心(简称“地心”)F2为一个焦点的椭圆,已知它的近地点A(长轴端点中离地面最近的点)距地面439km,远地点B(长轴端点中离地面最远的点)距地面2384km,AB是椭圆的长轴,地球的半径约6371km,求卫星运行的轨道方程。
变式拓展
万众瞩目的北京冬奥会将于2022年2月4日开幕,继2008年北京奥运会之后,国家体育场(又名鸟巢)将再次承办奥运会开幕式,在手工课上,王老师带领同学们一起制作了一个近似鸟巢的金属模型,其俯视图可近似看成是两个大小不同、扁平程度相同的椭圆,已知大椭圆的长轴长为40cm,短轴长为20cm,小椭圆的短轴长为10cm,则小椭圆的长轴长为_ ___cm。
数学练习
1、中心在坐标原点,焦点在x轴上,右焦点到短轴的端点的距离为2,到右顶点的距离为1的椭圆的标准方程为____________
数学练习
2、中心在坐标原点,焦点在坐标轴上,长轴长和短轴长分别为8和6的椭圆的标准方程为____________
数学练习
3、中心在坐标原点,一个焦点坐标为(0,5),短轴长为4的椭圆的标准方程为____________
数学练习
4、中心在坐标原点,焦点在坐标轴上,长轴长是短轴长的3倍,且经过点(3,0)的椭圆的标准方程为________
过程类似例2(2)
数学应用
例3、已知椭圆的一个焦点坐标为(6,0),点B、C是椭圆短轴的两个端点,△FBC是等边三角形,求椭圆的标准方程。
变式拓展
变式拓展
课堂检测
1、课本第85页练习第1、2题。
课堂检测
课堂检测
课堂检测
焦点三角形面积:
课堂检测
课堂小结
课堂小结
课堂小结
课堂小结
椭圆简单的几何性质(1)
复习回顾
复习回顾
问题情境
问题:观察椭圆 的形状,
(1)你能从图中看出椭圆上任意一点(x,y)的横坐标x和 纵坐标y的取值范围吗?
(2)椭圆具有怎样的对称性?
(3)椭圆上有哪些特殊点?
(4)椭圆还有哪些其它的几何性质?
数学建构
数学建构
数学建构
数学建构
数学建构
数学建构
数学建构
数学建构
活动探究
类型一 对椭圆的几何性质的认识
-5≤x≤5且-3≤y≤3
10
6
8
(±4,0)
(±5,0)(0,±3)
(±5,0)
x轴和y轴
(0,0)
数学练习
1、已知椭圆25x2+16y2=400,则它的范围为_________, 长轴长为_____,短轴长为_____,焦距为____,焦点坐标为_____,顶点坐标为__ _____,对称轴为_____,对称中心为____,离心率为______
2、已知椭圆4x2+3y2=12,则它的范围为____________,长轴长为____,短轴长为_____,焦距为____,焦点坐标为_____,顶点坐标为___ ____,对称轴为_____,对称中心为____,离心率为______
-4≤x≤4且-5≤y≤5
10
8
6
(0,±3)
(±4,0)(0,±5)
x轴和y轴
(0,0)
8
2
(0,±1)
x轴和y轴
(0,0)
活动探究
类型二 利用椭圆的几何性质求椭圆的标准方程
例2、根据下列条件分别求椭圆的标准方程。
活动探究
类型二 利用椭圆的几何性质求椭圆的标准方程
(2)长轴长是短轴长的3倍,且经过点(0,3);
例2、根据下列条件分别求椭圆的标准方程。
活动探究
类型二 利用椭圆的几何性质求椭圆的标准方程
(3)焦距是8,离心率为0.8;
例2、根据下列条件分别求椭圆的标准方程。
解:
活动探究
类型二 利用椭圆的几何性质求椭圆的标准方程
例2、根据下列条件分别求椭圆的标准方程。
活动探究
类型三 椭圆几何性质的实际应用
例4、我国发射的第一颗人造地球卫星的运行轨道是以地球的中心(简称“地心”)F2为一个焦点的椭圆,已知它的近地点A(长轴端点中离地面最近的点)距地面439km,远地点B(长轴端点中离地面最远的点)距地面2384km,AB是椭圆的长轴,地球的半径约6371km,求卫星运行的轨道方程。
变式拓展
万众瞩目的北京冬奥会将于2022年2月4日开幕,继2008年北京奥运会之后,国家体育场(又名鸟巢)将再次承办奥运会开幕式,在手工课上,王老师带领同学们一起制作了一个近似鸟巢的金属模型,其俯视图可近似看成是两个大小不同、扁平程度相同的椭圆,已知大椭圆的长轴长为40cm,短轴长为20cm,小椭圆的短轴长为10cm,则小椭圆的长轴长为_ ___cm。
数学练习
1、中心在坐标原点,焦点在x轴上,右焦点到短轴的端点的距离为2,到右顶点的距离为1的椭圆的标准方程为____________
数学练习
2、中心在坐标原点,焦点在坐标轴上,长轴长和短轴长分别为8和6的椭圆的标准方程为____________
数学练习
3、中心在坐标原点,一个焦点坐标为(0,5),短轴长为4的椭圆的标准方程为____________
数学练习
4、中心在坐标原点,焦点在坐标轴上,长轴长是短轴长的3倍,且经过点(3,0)的椭圆的标准方程为________
过程类似例2(2)
数学应用
例3、已知椭圆的一个焦点坐标为(6,0),点B、C是椭圆短轴的两个端点,△FBC是等边三角形,求椭圆的标准方程。
变式拓展
变式拓展
课堂检测
1、课本第85页练习第1、2题。
课堂检测
课堂检测
课堂检测
焦点三角形面积:
课堂检测
课堂小结
课堂小结
课堂小结
课堂小结
