3.1.2椭圆的几何性质(2)课件-2021-2022学年高二上学期苏教版选择性必修第一册(共48张PPT)
文档属性
| 名称 | 3.1.2椭圆的几何性质(2)课件-2021-2022学年高二上学期苏教版选择性必修第一册(共48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 17:58:41 | ||
图片预览









文档简介
(共48张PPT)
椭圆简单的几何性质(2)
复习回顾
复习回顾
复习回顾
复习回顾
问题诊断
1、椭圆(1-m)x2-my2=1的长轴长为_________
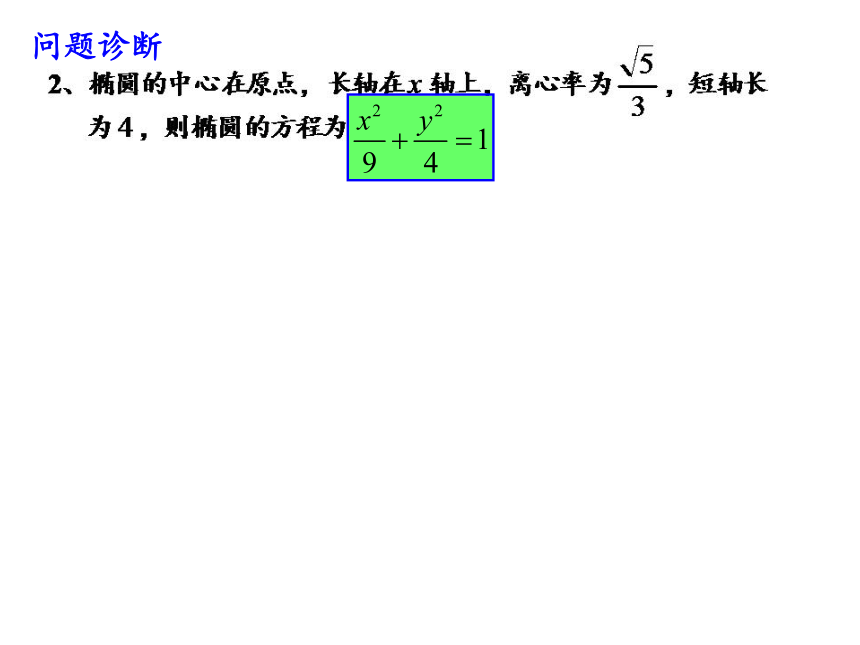
问题诊断
问题诊断
数学建构
1、求椭圆离心率的值或取值范围的常用方法
(3)方程法:若a、c的值不可求,则可根据条件建立关于a、b、c的关系式,借助于a2=b2+c2,转化为关于a、c的齐次方程(或不等式),再将方程(或不等式)两边同除以a的最高次幂,得到关于e的方程(或不等式),即可求得e的值(或取值范围)。
数学建构
2、椭圆上一点与椭圆上关于原点对称两点间的结论
PM、PN
PM、PN
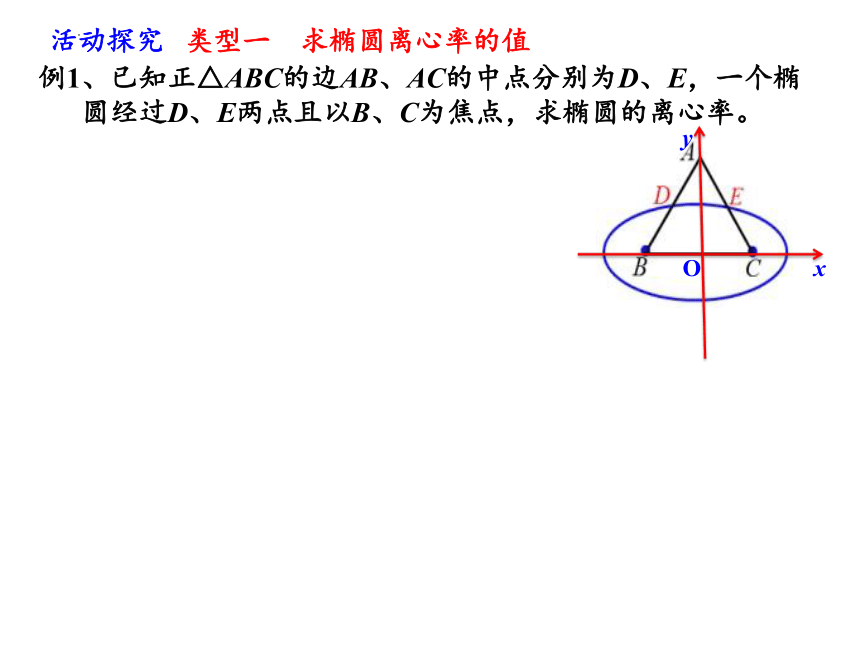
例1、已知正△ABC的边AB、AC的中点分别为D、E,一个椭圆经过D、E两点且以B、C为焦点,求椭圆的离心率。
活动探究
类型一 求椭圆离心率的值
O
x
y
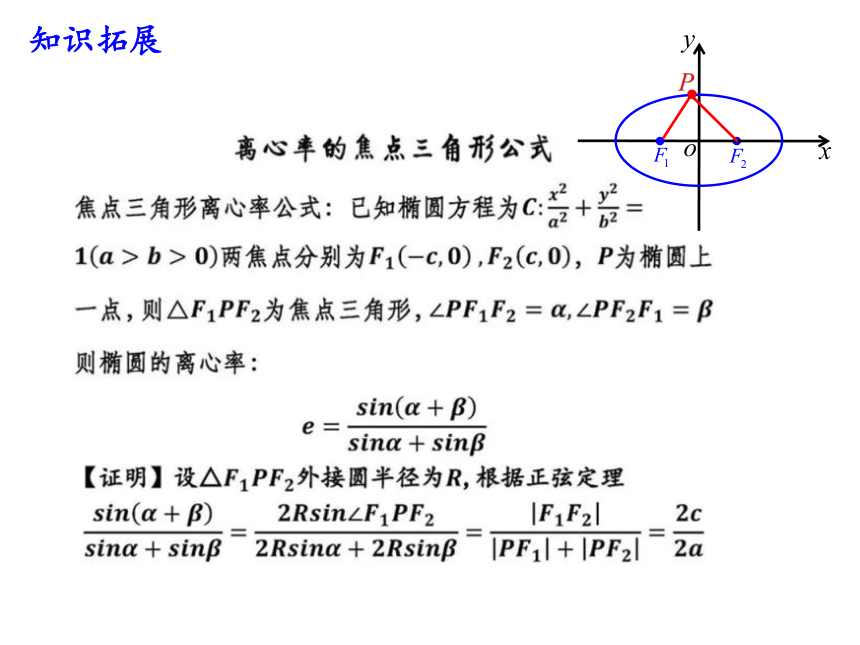
知识拓展
数学练习
1、若椭圆的焦距等于它的短轴长,则椭圆的离心率为__ __
数学练习
2、若椭圆的两个焦点及短轴的一个端点构成正三角形,则椭圆的离心率为________
数学练习
3、若椭圆的两个焦点把长轴长分成三等分,则椭圆的离心率为________
数学练习
4、将圆x2+y2=4上所有的点纵坐标保持不变,横坐标变为原来的一半,则所得曲线的离心率为______
活动探究
类型一 求椭圆离心率的值
例2、
数学练习
1、
数学练习
2、
例3、
活动探究
类型一 求椭圆离心率的值
H
数学练习
数学练习
数学练习
3、
例4、
活动探究
类型一 求椭圆离心率的值
变式拓展
F1
变式拓展
F1
活动探究
类型二 求椭圆离心率的取值范围
例5、
变式拓展
1、
变式拓展
2、
活动探究
类型二 求椭圆离心率的取值范围
例6、
法一:
活动探究
类型二 求椭圆离心率的取值范围
例6、
活动探究
类型二 求椭圆离心率的取值范围
例6、
变式拓展
例7、
活动探究
类型三 类型三 椭圆离心率问题的应用
可用特值法
(-a,0)
(a,0)
(x0,y0)
例7、
活动探究
类型三 类型三 椭圆离心率问题的应用
PM、PN
PM、PN
课堂检测
1、课本第85页练习第3、4、5、6题。
2、
课堂检测
3、
H
课堂检测
4、
链接高考
链接高考
链接高考
链接高考
课堂小结
课堂小结
课堂小结
课堂小结
4、求椭圆离心率的值或取值范围的常用方法
(3)方程法:若a、c的值不可求,则可根据条件建立关于a、b、c的关系式,借助于a2=b2+c2,转化为关于a、c的齐次方程(或不等式),再将方程(或不等式)两边同除以a的最高次幂,得到关于e的方程(或不等式),即可求得e的值(或取值范围)。
课堂小结
5、椭圆上一点与椭圆上关于原点对称两点间的结论
课堂小结
椭圆简单的几何性质(2)
复习回顾
复习回顾
复习回顾
复习回顾
问题诊断
1、椭圆(1-m)x2-my2=1的长轴长为_________
问题诊断
问题诊断
数学建构
1、求椭圆离心率的值或取值范围的常用方法
(3)方程法:若a、c的值不可求,则可根据条件建立关于a、b、c的关系式,借助于a2=b2+c2,转化为关于a、c的齐次方程(或不等式),再将方程(或不等式)两边同除以a的最高次幂,得到关于e的方程(或不等式),即可求得e的值(或取值范围)。
数学建构
2、椭圆上一点与椭圆上关于原点对称两点间的结论
PM、PN
PM、PN
例1、已知正△ABC的边AB、AC的中点分别为D、E,一个椭圆经过D、E两点且以B、C为焦点,求椭圆的离心率。
活动探究
类型一 求椭圆离心率的值
O
x
y
知识拓展
数学练习
1、若椭圆的焦距等于它的短轴长,则椭圆的离心率为__ __
数学练习
2、若椭圆的两个焦点及短轴的一个端点构成正三角形,则椭圆的离心率为________
数学练习
3、若椭圆的两个焦点把长轴长分成三等分,则椭圆的离心率为________
数学练习
4、将圆x2+y2=4上所有的点纵坐标保持不变,横坐标变为原来的一半,则所得曲线的离心率为______
活动探究
类型一 求椭圆离心率的值
例2、
数学练习
1、
数学练习
2、
例3、
活动探究
类型一 求椭圆离心率的值
H
数学练习
数学练习
数学练习
3、
例4、
活动探究
类型一 求椭圆离心率的值
变式拓展
F1
变式拓展
F1
活动探究
类型二 求椭圆离心率的取值范围
例5、
变式拓展
1、
变式拓展
2、
活动探究
类型二 求椭圆离心率的取值范围
例6、
法一:
活动探究
类型二 求椭圆离心率的取值范围
例6、
活动探究
类型二 求椭圆离心率的取值范围
例6、
变式拓展
例7、
活动探究
类型三 类型三 椭圆离心率问题的应用
可用特值法
(-a,0)
(a,0)
(x0,y0)
例7、
活动探究
类型三 类型三 椭圆离心率问题的应用
PM、PN
PM、PN
课堂检测
1、课本第85页练习第3、4、5、6题。
2、
课堂检测
3、
H
课堂检测
4、
链接高考
链接高考
链接高考
链接高考
课堂小结
课堂小结
课堂小结
课堂小结
4、求椭圆离心率的值或取值范围的常用方法
(3)方程法:若a、c的值不可求,则可根据条件建立关于a、b、c的关系式,借助于a2=b2+c2,转化为关于a、c的齐次方程(或不等式),再将方程(或不等式)两边同除以a的最高次幂,得到关于e的方程(或不等式),即可求得e的值(或取值范围)。
课堂小结
5、椭圆上一点与椭圆上关于原点对称两点间的结论
课堂小结
