6.5.1直线与平面垂直(第一课时)课件-2021-2022学年高一下学期数学北师大版(2019)必修第二册(共37张PPT)
文档属性
| 名称 | 6.5.1直线与平面垂直(第一课时)课件-2021-2022学年高一下学期数学北师大版(2019)必修第二册(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 00:00:00 | ||
图片预览









文档简介
(共37张PPT)
§ 6.5.1 直线与平面垂直
(第一课时)
北师大(2019)必修2
聚焦知识目标
1. 理解直线和平面垂直、平面与平面垂直的性质定理,并能用文字、符号和图形语言描述定理.(重点)
2.能应用线面垂直、面面垂直的性质定理证明相关问题.(重点、难点)
3.理解平行与垂直之间的相互转化.(易错点)
数学素养
1.通过学习直线与平面垂直的性质,提升直观想象、逻辑推理的数学核心素养.
2.通过学习平面与平面垂直的性质,提升直观想象、逻辑推理、数学运算的数学核心素养.
环节一
垂直的相关概念
环节二
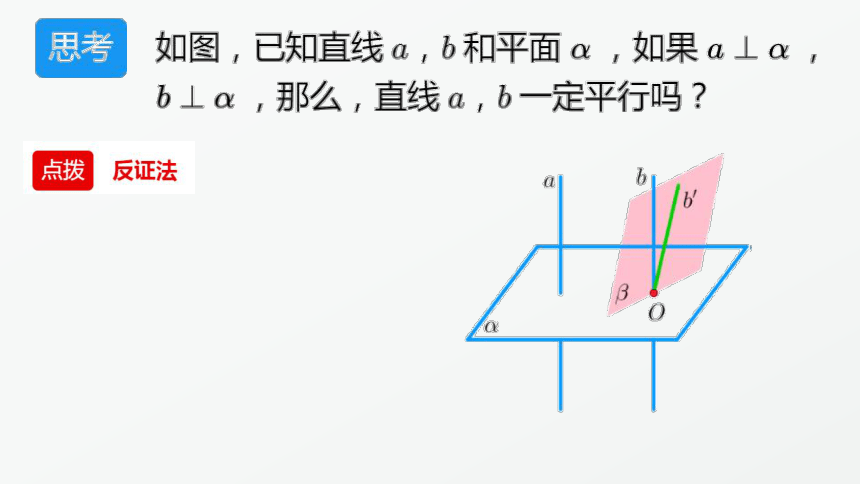
直线与平面垂直性质
体验1
例1
例2
例3
体验2
环节三
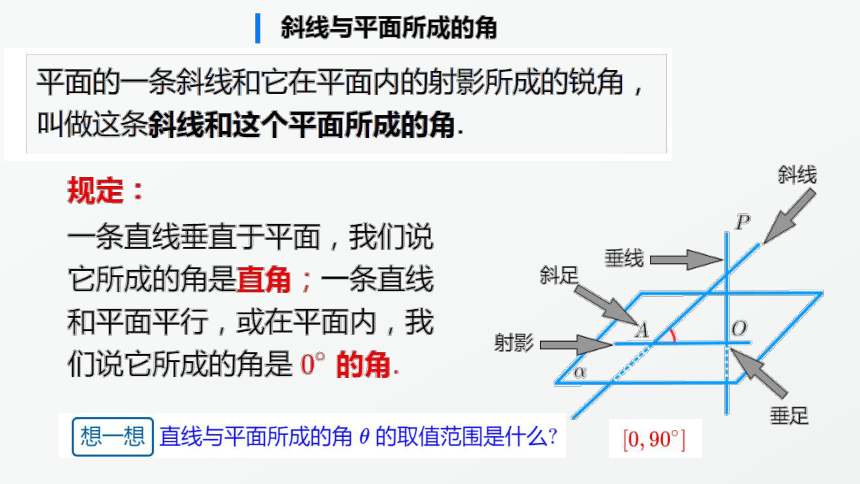
线面距离和角度
本章1.2节已提到从平面外一点作一个平面的垂线,这个点和垂足间的距离称为点到平面的距离.
请证明:如果一条直线平行一个平面,那么这条直线上各点到这个平面的距离都相等.
线面距离
直线与平面分别用l与 表示,且 l// .
要证明直线/上各点到平面 的距离相等,只要证明直线l上任意两点到平面α的距离相等.而点到平面α的距离也就是点到平面α垂线段的长。
过直线l上任意两点A,B分别作平面a的垂线,垂足分别为E.F.因为 AE⊥ ,BF ⊥ α,所以 AE//BF.
设过直线AE和BF的平面为β,则 β∩α=EF.
由l// 知l//EF,所以四边形AEFB是平行四边形。
所以AE=BF.即直线l上各点到平面α的距离相等.
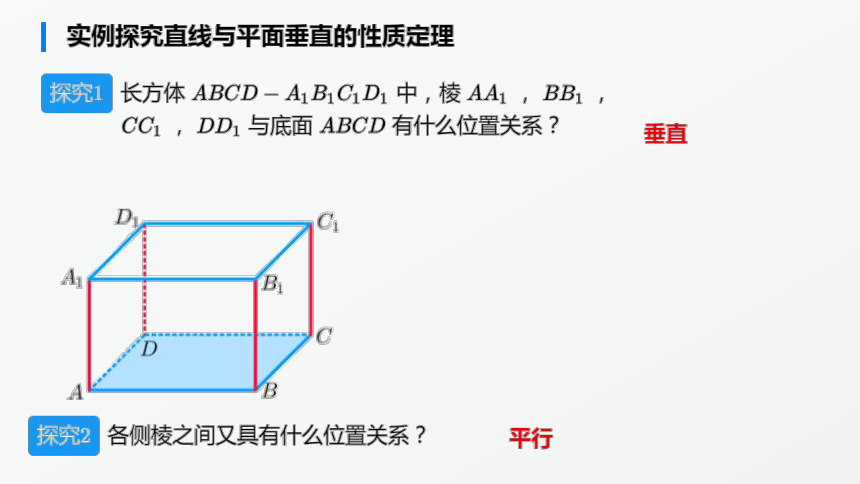
例4 如图.已知正方 体ABCD-A1 B1 C1 D1.
(1)求 D1 A与底面ABCD所成的角;A
(2)设正方体 ABCD-A1 B1 C1 D1的棱长为a,求 D1 B与底面ABCD所成的角的余弦值.
解 (1)因为 DD1⊥底面ABCD,所以 ∠D1 AD是 D1 A与底面ABCD所成的角.
因为侧面 A1 ADD1是正方形,所以 ∠D1 AD=45°.
即 D1 A与底面ABCD所成的角为 45°.
(2)如图,连接BD,则 BD= a.
因为 DD1三底面ABCD,所以∠ D1 BD是D1B与底面ABCD所成的角,同时 DD1⊥DB.利用直角三角形得 cos∠D1BD.
环节四
学以致用
1
2
3
4
5
§ 6.5.1 直线与平面垂直
(第一课时)
北师大(2019)必修2
聚焦知识目标
1. 理解直线和平面垂直、平面与平面垂直的性质定理,并能用文字、符号和图形语言描述定理.(重点)
2.能应用线面垂直、面面垂直的性质定理证明相关问题.(重点、难点)
3.理解平行与垂直之间的相互转化.(易错点)
数学素养
1.通过学习直线与平面垂直的性质,提升直观想象、逻辑推理的数学核心素养.
2.通过学习平面与平面垂直的性质,提升直观想象、逻辑推理、数学运算的数学核心素养.
环节一
垂直的相关概念
环节二
直线与平面垂直性质
体验1
例1
例2
例3
体验2
环节三
线面距离和角度
本章1.2节已提到从平面外一点作一个平面的垂线,这个点和垂足间的距离称为点到平面的距离.
请证明:如果一条直线平行一个平面,那么这条直线上各点到这个平面的距离都相等.
线面距离
直线与平面分别用l与 表示,且 l// .
要证明直线/上各点到平面 的距离相等,只要证明直线l上任意两点到平面α的距离相等.而点到平面α的距离也就是点到平面α垂线段的长。
过直线l上任意两点A,B分别作平面a的垂线,垂足分别为E.F.因为 AE⊥ ,BF ⊥ α,所以 AE//BF.
设过直线AE和BF的平面为β,则 β∩α=EF.
由l// 知l//EF,所以四边形AEFB是平行四边形。
所以AE=BF.即直线l上各点到平面α的距离相等.
例4 如图.已知正方 体ABCD-A1 B1 C1 D1.
(1)求 D1 A与底面ABCD所成的角;A
(2)设正方体 ABCD-A1 B1 C1 D1的棱长为a,求 D1 B与底面ABCD所成的角的余弦值.
解 (1)因为 DD1⊥底面ABCD,所以 ∠D1 AD是 D1 A与底面ABCD所成的角.
因为侧面 A1 ADD1是正方形,所以 ∠D1 AD=45°.
即 D1 A与底面ABCD所成的角为 45°.
(2)如图,连接BD,则 BD= a.
因为 DD1三底面ABCD,所以∠ D1 BD是D1B与底面ABCD所成的角,同时 DD1⊥DB.利用直角三角形得 cos∠D1BD.
环节四
学以致用
1
2
3
4
5
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
