第九章 统计 章末总结 课件(共33张PPT)
文档属性
| 名称 | 第九章 统计 章末总结 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 853.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 00:00:00 | ||
图片预览





文档简介
(共33张PPT)
章末总结
网络构建·归纳整合
题型归纳·素养提升
网络构建·归纳整合
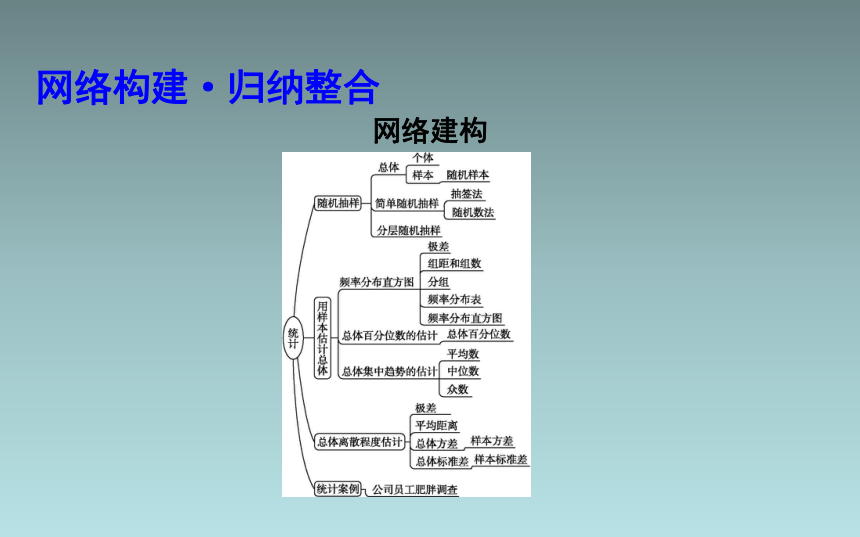
网络建构
知识辨析
判断下列说法是否正确.(请在括号中填“√”或“×”)
1.抽签法和随机数法都是不放回抽样.( )
2.抽签法抽签时,先抽签的人占便宜.( )
3.利用随机数表抽样时,开始位置和读数方向可以任意选择.( )
4.分层随机抽样中,为确保公平性,在每层都应用同一抽样方法.( )
5.频率分布直方图中每个小长方形的面积等于相应组的频率,各个小长方形面积之和小于1.( )
6.从总体中抽取一个样本,用样本的分布估计总体的分布,样本容量越小估计越准确.( )
7.在样本数据中,频率分布最大值所对应的样本数据是众数.( )
√
×
√
×
×
×
√
题型归纳·素养提升
题型一 随机抽样
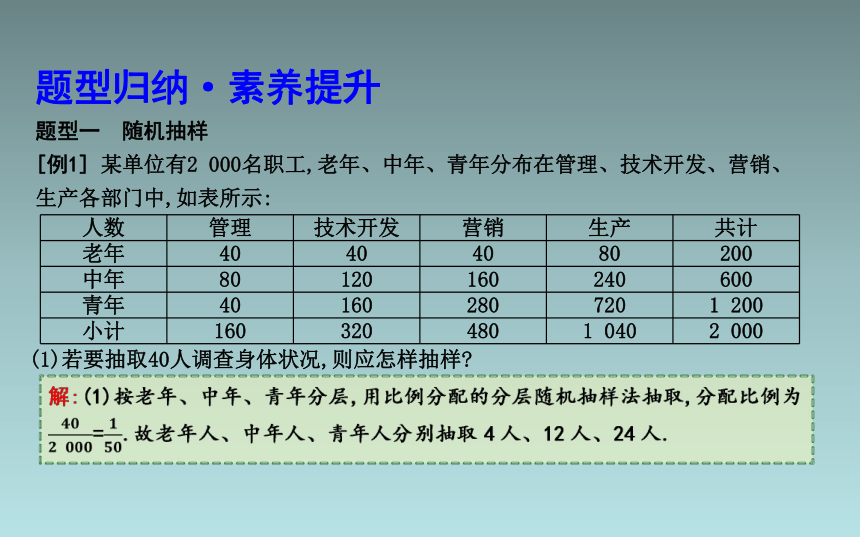
[例1] 某单位有2 000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如表所示:
人数 管理 技术开发 营销 生产 共计
老年 40 40 40 80 200
中年 80 120 160 240 600
青年 40 160 280 720 1 200
小计 160 320 480 1 040 2 000
(1)若要抽取40人调查身体状况,则应怎样抽样
[例1] 某单位有2 000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如表所示:
人数 管理 技术开发 营销 生产 共计
老年 40 40 40 80 200
中年 80 120 160 240 600
青年 40 160 280 720 1 200
小计 160 320 480 1 040 2 000
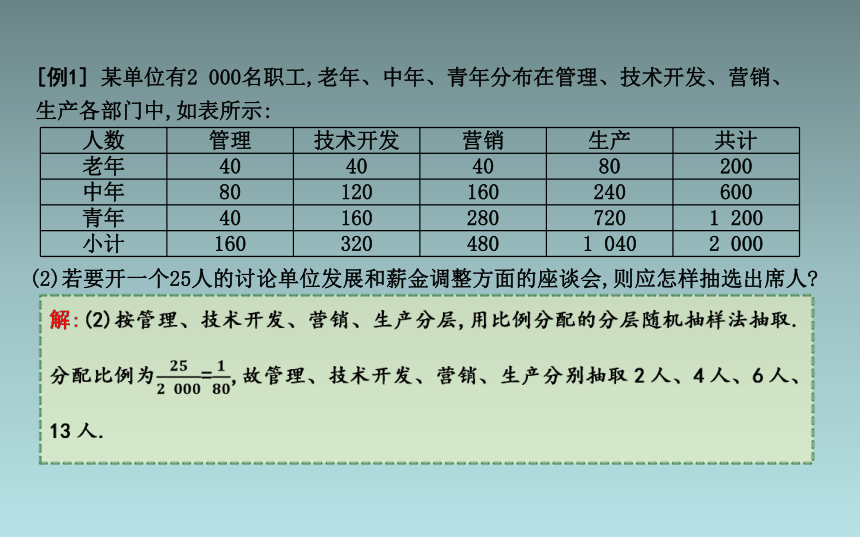
(2)若要开一个25人的讨论单位发展和薪金调整方面的座谈会,则应怎样抽选出席人
[例1] 某单位有2 000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如表所示:
人数 管理 技术开发 营销 生产 共计
老年 40 40 40 80 200
中年 80 120 160 240 600
青年 40 160 280 720 1 200
小计 160 320 480 1 040 2 000
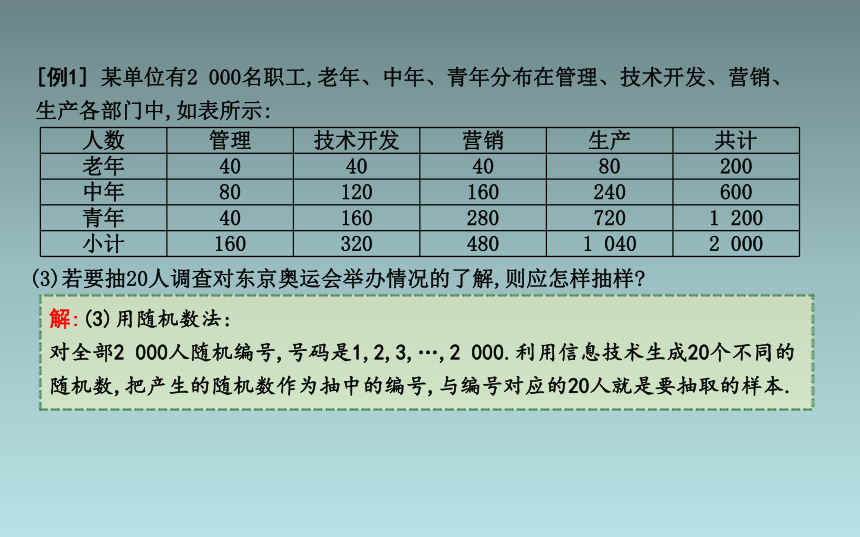
(3)若要抽20人调查对东京奥运会举办情况的了解,则应怎样抽样
解:(3)用随机数法:
对全部2 000人随机编号,号码是1,2,3,…,2 000.利用信息技术生成20个不同的随机数,把产生的随机数作为抽中的编号,与编号对应的20人就是要抽取的样本.
方法总结
研究统计问题的基本思想方法就是从总体中抽取样本,用样本估计总体,因此选择适当的抽样方法抽取具有代表性的样本对整个统计问题起着至关重要的作用.
简单随机抽样是最简单和最基本的抽样方法.在进行分层随机抽样时要用到简单随机抽样方法.当总体中的个体数较少时,常采用简单随机抽样;当已知总体由差异明显的几部分组成时,常采用分层随机抽样.实现简单随机抽样,常用抽签法和随机数法.
跟踪训练1:问题:①某小区有800户家庭,其中高收入家庭200户,中等收入家庭480户,低收入家庭120户,为了了解有关家用轿车购买力的某个指标,要从中抽取一个容量为100的样本;②从10名学生中抽取3人参加座谈会.方法:(1)简单随机抽样;(2)分层随机抽样.则问题与方法配对正确的是( )
(A)①(1),②(2) (B)①(2),②(1)
(C)①(1),②(1) (D)①(2),②(2)
解析:问题①中的总体是由差异明显的几部分组成的,故可采用分层随机抽样方法;问题②中总体的个数较少,故可采用简单随机抽样.故选B.
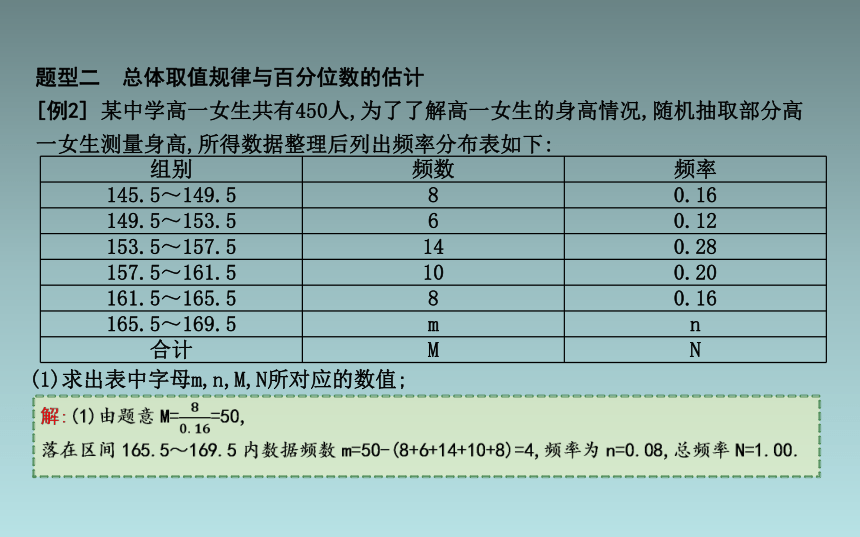
题型二 总体取值规律与百分位数的估计
[例2] 某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
组别 频数 频率
145.5~149.5 8 0.16
149.5~153.5 6 0.12
153.5~157.5 14 0.28
157.5~161.5 10 0.20
161.5~165.5 8 0.16
165.5~169.5 m n
合计 M N
(1)求出表中字母m,n,M,N所对应的数值;
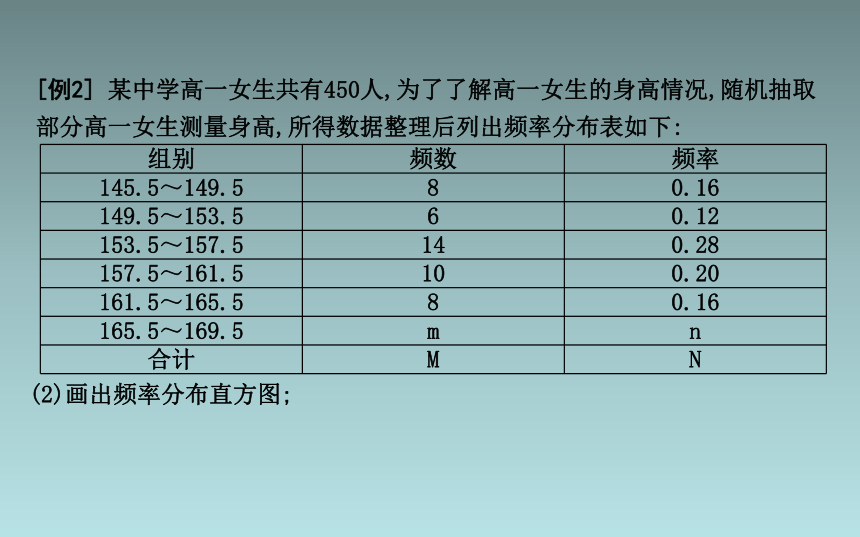
[例2] 某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
组别 频数 频率
145.5~149.5 8 0.16
149.5~153.5 6 0.12
153.5~157.5 14 0.28
157.5~161.5 10 0.20
161.5~165.5 8 0.16
165.5~169.5 m n
合计 M N
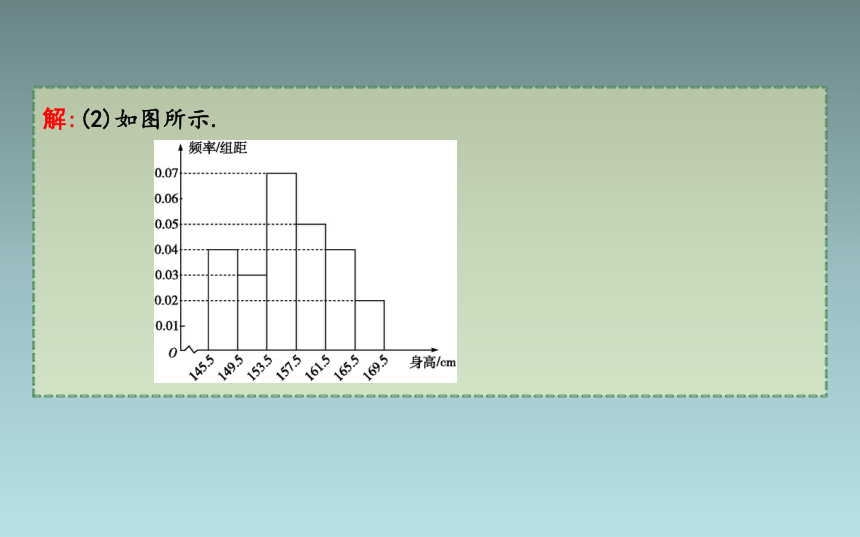
(2)画出频率分布直方图;
解:(2)如图所示.
[例2] 某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
组别 频数 频率
145.5~149.5 8 0.16
149.5~153.5 6 0.12
153.5~157.5 14 0.28
157.5~161.5 10 0.20
161.5~165.5 8 0.16
165.5~169.5 m n
合计 M N
(3)估计该校高一女生身高在149.5 cm~165.5 cm范围内有多少人.
解:(3)该所学校高一女生身高在149.5 cm~165.5 cm范围内的频率为0.12+0.28+
0.20+0.16=0.76,则该校高一女生在此范围内的人数约为450×0.76=342(人).
[例2] 某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
组别 频数 频率
145.5~149.5 8 0.16
149.5~153.5 6 0.12
153.5~157.5 14 0.28
157.5~161.5 10 0.20
161.5~165.5 8 0.16
165.5~169.5 m n
合计 M N
(4)估计该校高一女生身高的第80百分位数.
方法总结
与频率分布直方图有关问题的常见类型及解题策略
(1)已知频率分布直方图中的部分数据,求其他数据,可根据频率分布直方图中的数据求出样本与整体的关系,利用频率之和等于1就可求出其他数据.
(2)已知频率分布直方图,求某种范围内的数据,可利用图形及某范围结合
求解.
(3)已知频率分布直方图,估计总体的第p百分位数,可利用累计频率估计第p百分位数所在的小组,再把本组数据看成均匀分布计算.
跟踪训练2:高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如表所示的频率分布表:
分组 频数 频率
[85,95) ① ②
[95,105) 0.050
[105,115) 0.200
[115,125) 12 0.300
[125,135) 0.275
[135,145) 4 ③
[145,155] 0.050
合计 ④
(1)表格中①②③④处的数值分别为 , , , ;
跟踪训练2:高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如表所示的频率分布表:
分组 频数 频率
[85,95) ① ②
[95,105) 0.050
[105,115) 0.200
[115,125) 12 0.300
[125,135) 0.275
[135,145) 4 ③
[145,155] 0.050
合计 ④
(2)在图中画出[85,155]的频率分布直方图;
解:(2)频率分布直方图如图所示.
跟踪训练2:高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如表所示的频率分布表:
分组 频数 频率
[85,95) ① ②
[95,105) 0.050
[105,115) 0.200
[115,125) 12 0.300
[125,135) 0.275
[135,145) 4 ③
[145,155] 0.050
合计 ④
(3)根据题中信息估计总体数学成绩的60%分位数.
题型三 总体集中趋势与离散程度的估计
[例3] 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩(单位:环)如图所示.
(1)填写下表.
平均数 方差 中位数 命中9环以上
(包括9环)
甲 7 1.2 1
乙 5.4 3
题型三 总体集中趋势与离散程度的估计
[例3] 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩(单位:环)如图所示.
(2)请从以下四个不同的角度对这次测试进行分析.
①从平均数和方差分析偏离程度;
[例3] 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩(单位:环)如图所示.
(2)请从以下四个不同的角度对这次测试进行分析.
②从平均数和中位数分析谁的成绩好些;
解:②甲、乙平均水平相同,而乙的中位数比甲大,可见乙射靶环数的优秀次数比甲多.
[例3] 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩(单位:环)如图所示.
(2)请从以下四个不同的角度对这次测试进行分析.
③从平均数和命中9环以上(包括9环)的次数分析谁的成绩好些;
解:③甲、乙平均水平相同,而乙命中9环以上(包括9环)的次数比甲多2次,可见乙的射靶成绩比甲好.
[例3] 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩(单位:环)如图所示.
(2)请从以下四个不同的角度对这次测试进行分析.
④从折线图上两人射击命中环数及走势分析谁更有潜力.
解:④从折线图上看,乙的成绩呈上升趋势,而甲的成绩在平均线上波动不大,说明乙的状态在提升,有潜力可挖.
方法总结
平均数、中位数和众数从不同角度刻画数据的集中趋势;极差、方差和标准差都是刻画数据的离散程度,一组数据的方差或标准差越大,说明这组数据的离散程度越大.
跟踪训练3:(2021·安徽蚌埠高一期末)某工厂有工人1 000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层随机抽样方法(按A类、B类分两层)从该工厂的工人中共抽取100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(1)A类工人和B类工人各抽取多少人
跟踪训练3:(2021·安徽蚌埠高一期末)某工厂有工人1 000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层随机抽样方法(按A类、B类分两层)从该工厂的工人中共抽取100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(2)将A类工人和B类工人的抽查结果分别绘制成频率分布直方图(如图1和图2).
①就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小 (不用计算,可通过观察直方图直接回答结论)
解:(2)①从直方图可以判断:B类工人中个体间的差异程度更小.
跟踪训练3:(2021·安徽蚌埠高一期末)某工厂有工人1 000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层随机抽样方法(按A类、B类分两层)从该工厂的工人中共抽取100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(2)将A类工人和B类工人的抽查结果分别绘制成频率分布直方图(如图1和图2).
②分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表).
章末总结
网络构建·归纳整合
题型归纳·素养提升
网络构建·归纳整合
网络建构
知识辨析
判断下列说法是否正确.(请在括号中填“√”或“×”)
1.抽签法和随机数法都是不放回抽样.( )
2.抽签法抽签时,先抽签的人占便宜.( )
3.利用随机数表抽样时,开始位置和读数方向可以任意选择.( )
4.分层随机抽样中,为确保公平性,在每层都应用同一抽样方法.( )
5.频率分布直方图中每个小长方形的面积等于相应组的频率,各个小长方形面积之和小于1.( )
6.从总体中抽取一个样本,用样本的分布估计总体的分布,样本容量越小估计越准确.( )
7.在样本数据中,频率分布最大值所对应的样本数据是众数.( )
√
×
√
×
×
×
√
题型归纳·素养提升
题型一 随机抽样
[例1] 某单位有2 000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如表所示:
人数 管理 技术开发 营销 生产 共计
老年 40 40 40 80 200
中年 80 120 160 240 600
青年 40 160 280 720 1 200
小计 160 320 480 1 040 2 000
(1)若要抽取40人调查身体状况,则应怎样抽样
[例1] 某单位有2 000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如表所示:
人数 管理 技术开发 营销 生产 共计
老年 40 40 40 80 200
中年 80 120 160 240 600
青年 40 160 280 720 1 200
小计 160 320 480 1 040 2 000
(2)若要开一个25人的讨论单位发展和薪金调整方面的座谈会,则应怎样抽选出席人
[例1] 某单位有2 000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如表所示:
人数 管理 技术开发 营销 生产 共计
老年 40 40 40 80 200
中年 80 120 160 240 600
青年 40 160 280 720 1 200
小计 160 320 480 1 040 2 000
(3)若要抽20人调查对东京奥运会举办情况的了解,则应怎样抽样
解:(3)用随机数法:
对全部2 000人随机编号,号码是1,2,3,…,2 000.利用信息技术生成20个不同的随机数,把产生的随机数作为抽中的编号,与编号对应的20人就是要抽取的样本.
方法总结
研究统计问题的基本思想方法就是从总体中抽取样本,用样本估计总体,因此选择适当的抽样方法抽取具有代表性的样本对整个统计问题起着至关重要的作用.
简单随机抽样是最简单和最基本的抽样方法.在进行分层随机抽样时要用到简单随机抽样方法.当总体中的个体数较少时,常采用简单随机抽样;当已知总体由差异明显的几部分组成时,常采用分层随机抽样.实现简单随机抽样,常用抽签法和随机数法.
跟踪训练1:问题:①某小区有800户家庭,其中高收入家庭200户,中等收入家庭480户,低收入家庭120户,为了了解有关家用轿车购买力的某个指标,要从中抽取一个容量为100的样本;②从10名学生中抽取3人参加座谈会.方法:(1)简单随机抽样;(2)分层随机抽样.则问题与方法配对正确的是( )
(A)①(1),②(2) (B)①(2),②(1)
(C)①(1),②(1) (D)①(2),②(2)
解析:问题①中的总体是由差异明显的几部分组成的,故可采用分层随机抽样方法;问题②中总体的个数较少,故可采用简单随机抽样.故选B.
题型二 总体取值规律与百分位数的估计
[例2] 某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
组别 频数 频率
145.5~149.5 8 0.16
149.5~153.5 6 0.12
153.5~157.5 14 0.28
157.5~161.5 10 0.20
161.5~165.5 8 0.16
165.5~169.5 m n
合计 M N
(1)求出表中字母m,n,M,N所对应的数值;
[例2] 某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
组别 频数 频率
145.5~149.5 8 0.16
149.5~153.5 6 0.12
153.5~157.5 14 0.28
157.5~161.5 10 0.20
161.5~165.5 8 0.16
165.5~169.5 m n
合计 M N
(2)画出频率分布直方图;
解:(2)如图所示.
[例2] 某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
组别 频数 频率
145.5~149.5 8 0.16
149.5~153.5 6 0.12
153.5~157.5 14 0.28
157.5~161.5 10 0.20
161.5~165.5 8 0.16
165.5~169.5 m n
合计 M N
(3)估计该校高一女生身高在149.5 cm~165.5 cm范围内有多少人.
解:(3)该所学校高一女生身高在149.5 cm~165.5 cm范围内的频率为0.12+0.28+
0.20+0.16=0.76,则该校高一女生在此范围内的人数约为450×0.76=342(人).
[例2] 某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
组别 频数 频率
145.5~149.5 8 0.16
149.5~153.5 6 0.12
153.5~157.5 14 0.28
157.5~161.5 10 0.20
161.5~165.5 8 0.16
165.5~169.5 m n
合计 M N
(4)估计该校高一女生身高的第80百分位数.
方法总结
与频率分布直方图有关问题的常见类型及解题策略
(1)已知频率分布直方图中的部分数据,求其他数据,可根据频率分布直方图中的数据求出样本与整体的关系,利用频率之和等于1就可求出其他数据.
(2)已知频率分布直方图,求某种范围内的数据,可利用图形及某范围结合
求解.
(3)已知频率分布直方图,估计总体的第p百分位数,可利用累计频率估计第p百分位数所在的小组,再把本组数据看成均匀分布计算.
跟踪训练2:高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如表所示的频率分布表:
分组 频数 频率
[85,95) ① ②
[95,105) 0.050
[105,115) 0.200
[115,125) 12 0.300
[125,135) 0.275
[135,145) 4 ③
[145,155] 0.050
合计 ④
(1)表格中①②③④处的数值分别为 , , , ;
跟踪训练2:高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如表所示的频率分布表:
分组 频数 频率
[85,95) ① ②
[95,105) 0.050
[105,115) 0.200
[115,125) 12 0.300
[125,135) 0.275
[135,145) 4 ③
[145,155] 0.050
合计 ④
(2)在图中画出[85,155]的频率分布直方图;
解:(2)频率分布直方图如图所示.
跟踪训练2:高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如表所示的频率分布表:
分组 频数 频率
[85,95) ① ②
[95,105) 0.050
[105,115) 0.200
[115,125) 12 0.300
[125,135) 0.275
[135,145) 4 ③
[145,155] 0.050
合计 ④
(3)根据题中信息估计总体数学成绩的60%分位数.
题型三 总体集中趋势与离散程度的估计
[例3] 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩(单位:环)如图所示.
(1)填写下表.
平均数 方差 中位数 命中9环以上
(包括9环)
甲 7 1.2 1
乙 5.4 3
题型三 总体集中趋势与离散程度的估计
[例3] 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩(单位:环)如图所示.
(2)请从以下四个不同的角度对这次测试进行分析.
①从平均数和方差分析偏离程度;
[例3] 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩(单位:环)如图所示.
(2)请从以下四个不同的角度对这次测试进行分析.
②从平均数和中位数分析谁的成绩好些;
解:②甲、乙平均水平相同,而乙的中位数比甲大,可见乙射靶环数的优秀次数比甲多.
[例3] 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩(单位:环)如图所示.
(2)请从以下四个不同的角度对这次测试进行分析.
③从平均数和命中9环以上(包括9环)的次数分析谁的成绩好些;
解:③甲、乙平均水平相同,而乙命中9环以上(包括9环)的次数比甲多2次,可见乙的射靶成绩比甲好.
[例3] 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩(单位:环)如图所示.
(2)请从以下四个不同的角度对这次测试进行分析.
④从折线图上两人射击命中环数及走势分析谁更有潜力.
解:④从折线图上看,乙的成绩呈上升趋势,而甲的成绩在平均线上波动不大,说明乙的状态在提升,有潜力可挖.
方法总结
平均数、中位数和众数从不同角度刻画数据的集中趋势;极差、方差和标准差都是刻画数据的离散程度,一组数据的方差或标准差越大,说明这组数据的离散程度越大.
跟踪训练3:(2021·安徽蚌埠高一期末)某工厂有工人1 000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层随机抽样方法(按A类、B类分两层)从该工厂的工人中共抽取100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(1)A类工人和B类工人各抽取多少人
跟踪训练3:(2021·安徽蚌埠高一期末)某工厂有工人1 000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层随机抽样方法(按A类、B类分两层)从该工厂的工人中共抽取100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(2)将A类工人和B类工人的抽查结果分别绘制成频率分布直方图(如图1和图2).
①就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小 (不用计算,可通过观察直方图直接回答结论)
解:(2)①从直方图可以判断:B类工人中个体间的差异程度更小.
跟踪训练3:(2021·安徽蚌埠高一期末)某工厂有工人1 000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层随机抽样方法(按A类、B类分两层)从该工厂的工人中共抽取100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(2)将A类工人和B类工人的抽查结果分别绘制成频率分布直方图(如图1和图2).
②分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表).
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
