小学数学 北师大版 四年级下册 二 认识三角形和四边形《探索与发现:三角形内角和》(共20张PPT)
文档属性
| 名称 | 小学数学 北师大版 四年级下册 二 认识三角形和四边形《探索与发现:三角形内角和》(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 17:19:36 | ||
图片预览




文档简介
(共20张PPT)
2.3 探索与发现:
三角形内角和
是这样吗?
我的三个内角的和一定比你大。
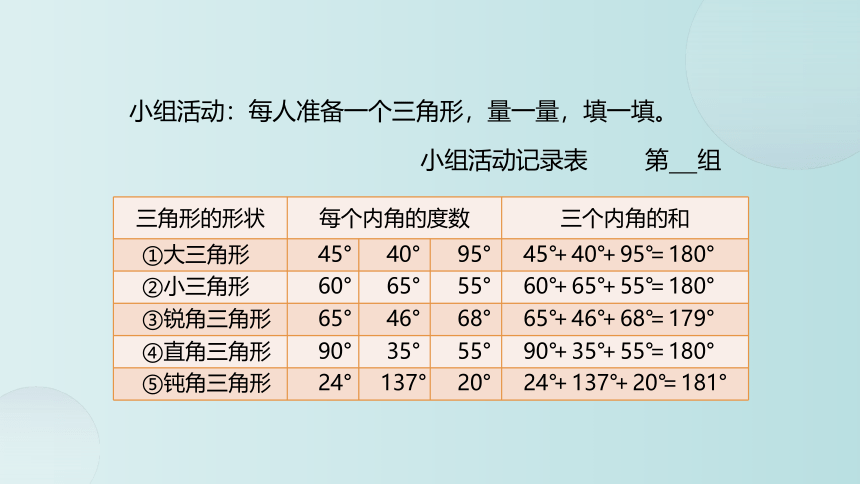
小组活动:每人准备一个三角形,量一量,填一填。
三角形的形状 每个内角的度数 三个内角的和
小组活动记录表
第 组
①大三角形
②小三角形
③锐角三角形
④直角三角形
⑤钝角三角形
45°
60°
65°
90°
24°
40°
65°
46°
35°
137°
95°
55°
68°
55°
20°
45°+40°+95°=180°
60°+65°+55°=180°
65°+46°+68°=179°
90°+35°+55°=180°
24°+137°+20°=181°
小组交流发现了什么。
我们发现每一个三角形的内角和都在180°左右。
实际上,三角形的三个内角和就是180°,只是因为测量有误差,造成比180°稍多或稍少。
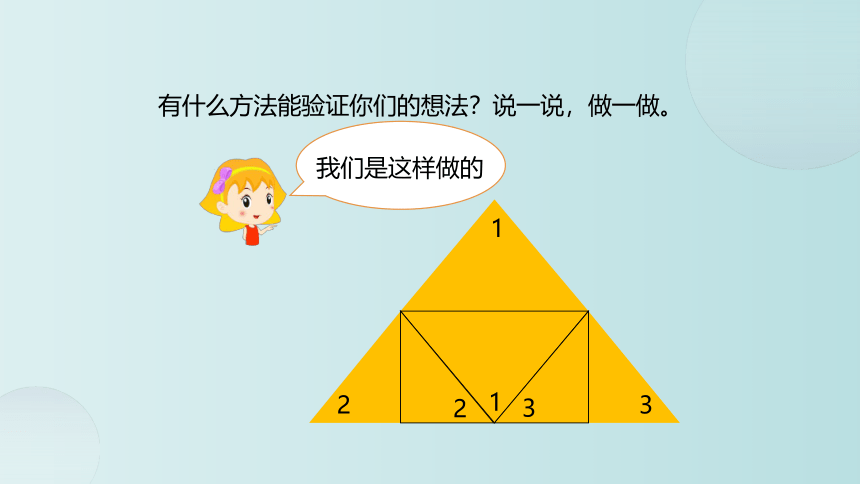
有什么方法能验证你们的想法?说一说,做一做。
180°是一个平角。我们把三角形的三个角撕下来,拼在一起。
有什么方法能验证你们的想法?说一说,做一做。
1
1
2
2
3
3
我们是这样做的
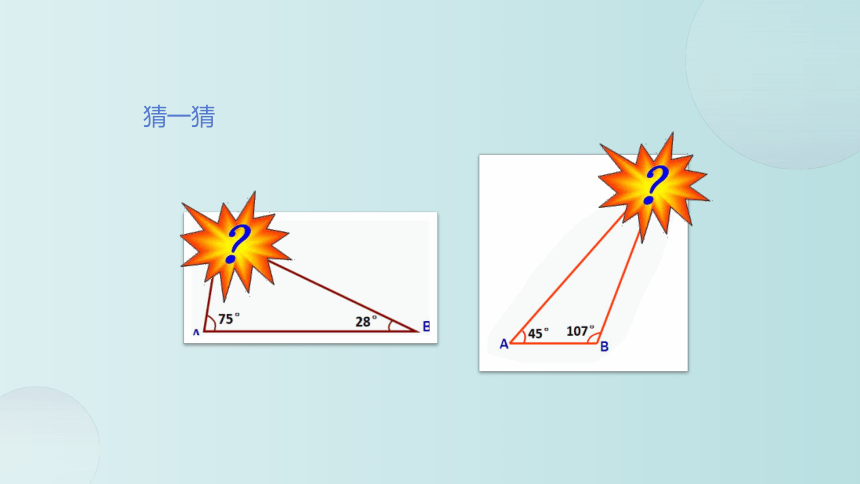
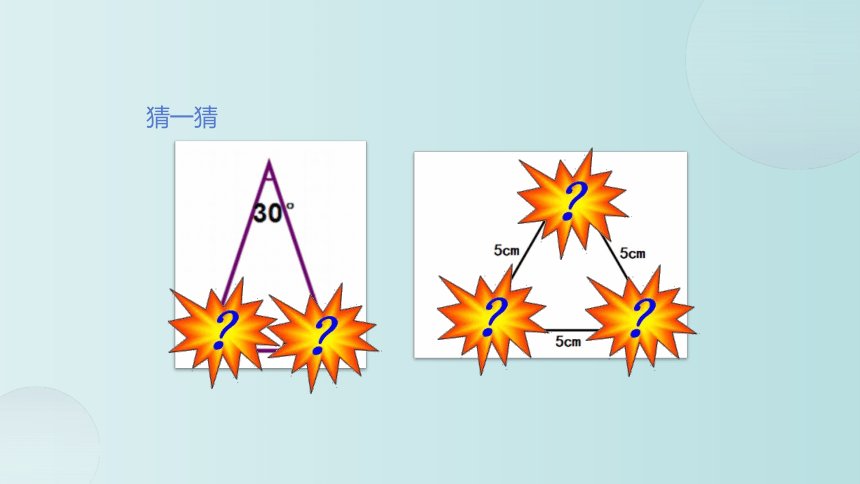
猜一猜
猜一猜
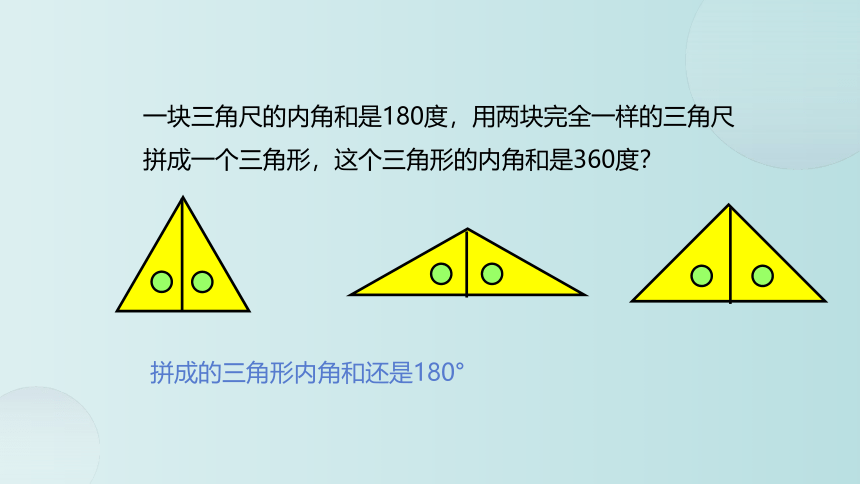
一块三角尺的内角和是180度,用两块完全一样的三角尺拼成一个三角形,这个三角形的内角和是360度?
拼成的三角形内角和还是180°
练一练(一)
1.填一填。
(1)
三角形ABC的内角和=∠A+∠B+∠C=( )+( )+( )=( ),所以三角形的内角和是( )。
(2)一个等边三角形的内角和是( )°,每个角都是( )°。
30°
90°
60°
180°
180°
180
60
2.选择。
(1)下面( )的内角和不是180°。
A. B. C. D.
(2)下面每组中三个度数的角不是一个三角形的三个内角的是( )。
A.120°15°35° B.90°45°45° C.60°60°60° D.160°10°10°
(3)把一个三角形的三条边分别扩大到原来的2倍,它的三个内角的度数( )。
A.分别扩大到原来的2倍 B.不变
C.分别缩小到原来的 D.无法确定
C
A
B
3.笑笑用两个完全相同的三角尺分别拼成两个不同的大三角形,请你算一算,每个大三角形的内角和是180°吗?
正确解答:
是180°。
思路分析:第一种拼法上面的角是两个30°的角拼成的,也就是60°,左右两个角都是60°,所以这个三角形的内角和是30°+30°+60°+60°=180°。第二种拼法上面的角是两个60°的角拼成的,也就是120°,左右两个角都是30°,所以这个三角形的内角和是60°+60°+30°+30°=180°。
4.【思维拓展题】下面各图形的内角和分别是多少度?
正确解答:
360° 540°
思路分析:如图,左边的四边形可以分割成2个三角形,所以内角和是180°×2=360°,右边的五边形可以分割成3个三角形,所以内角和是180°×3=540°。
练一练(2)
1.填空。
(1)在直角三角形中,两个锐角的度数和是( )°。
(2)(成都市锦江区)一个三角形的两个角的度数和是85°,这个三角形的第三个角的度数是( )°,这个三角形是( )三角形。
2.它们画的分别是什么三角形?(选题源自《小学教材全练》16页2题)
田田画的是_________________ _;萝萝画的是__________________。
90
95
180
钝角三角形或等腰三角形
锐角三角形
3.(合肥市政务区)下面是两块三角形玻璃打碎后留下的碎片,你知道它们原来各是什么三角形吗?
正确解答:
钝角三角形 锐角三角形或等边三角形
思路分析:因为三角形的内角和是180°,所以可以根据已知角的度数和三角形的内角和求出未知角的度数,从而判断出它们原来各是什么三角形。
4.埃及金字塔的四个侧面的形状都是等腰三角形,每个等腰三角形的顶角约是52°。埃及金字塔每个侧面的底角大约是多少度?
正确解答:
(180°-52°)÷2=64°
答:埃及金字塔每个侧面的底角大约是64°。
思路分析:根据三角形的内角和是180°及等腰三角形的两个底角度数相等,即可求出埃及金字塔每个侧面的底角大约是多少度。
5.刘大爷家有一块直角三角形菜地,在这块直角三角形菜地中,较大锐角的度数是较小锐角的2倍,你知道这块菜地三个角的度数吗?
正确解答:
90°÷(2+1)=30°
30°×2=60°
答:这块菜地三个角的度数分别是30°,60°,90°。
思路分析:可以通过画图来整理题中的数量关系,如下图:
较大锐角和较小锐角的度数和是90°,其中较小锐角占1份,较大锐角占2份,90°÷(2+1)=30°,即较小锐角的度数为30°,则较大锐角的度数为30°×2=60°。
6.【思维拓展题】如下图,等边三角形内有一个等腰三角形,并且∠1=∠2,∠3=∠4,求∠5的度数。
正确解答:
∠5=120°
思路分析:因为大三角形是等边三角形,所以∠1+∠2=∠3+∠4=60°。又因为∠1=∠2,∠3=∠4,所以2∠1=2∠3=60°,∠1=∠3=60°÷2=30°。在等腰三角形中,∠1+∠3=60°,∠5=180°-(∠1+∠3)=180°-60°=120°。
2.3 探索与发现:
三角形内角和
是这样吗?
我的三个内角的和一定比你大。
小组活动:每人准备一个三角形,量一量,填一填。
三角形的形状 每个内角的度数 三个内角的和
小组活动记录表
第 组
①大三角形
②小三角形
③锐角三角形
④直角三角形
⑤钝角三角形
45°
60°
65°
90°
24°
40°
65°
46°
35°
137°
95°
55°
68°
55°
20°
45°+40°+95°=180°
60°+65°+55°=180°
65°+46°+68°=179°
90°+35°+55°=180°
24°+137°+20°=181°
小组交流发现了什么。
我们发现每一个三角形的内角和都在180°左右。
实际上,三角形的三个内角和就是180°,只是因为测量有误差,造成比180°稍多或稍少。
有什么方法能验证你们的想法?说一说,做一做。
180°是一个平角。我们把三角形的三个角撕下来,拼在一起。
有什么方法能验证你们的想法?说一说,做一做。
1
1
2
2
3
3
我们是这样做的
猜一猜
猜一猜
一块三角尺的内角和是180度,用两块完全一样的三角尺拼成一个三角形,这个三角形的内角和是360度?
拼成的三角形内角和还是180°
练一练(一)
1.填一填。
(1)
三角形ABC的内角和=∠A+∠B+∠C=( )+( )+( )=( ),所以三角形的内角和是( )。
(2)一个等边三角形的内角和是( )°,每个角都是( )°。
30°
90°
60°
180°
180°
180
60
2.选择。
(1)下面( )的内角和不是180°。
A. B. C. D.
(2)下面每组中三个度数的角不是一个三角形的三个内角的是( )。
A.120°15°35° B.90°45°45° C.60°60°60° D.160°10°10°
(3)把一个三角形的三条边分别扩大到原来的2倍,它的三个内角的度数( )。
A.分别扩大到原来的2倍 B.不变
C.分别缩小到原来的 D.无法确定
C
A
B
3.笑笑用两个完全相同的三角尺分别拼成两个不同的大三角形,请你算一算,每个大三角形的内角和是180°吗?
正确解答:
是180°。
思路分析:第一种拼法上面的角是两个30°的角拼成的,也就是60°,左右两个角都是60°,所以这个三角形的内角和是30°+30°+60°+60°=180°。第二种拼法上面的角是两个60°的角拼成的,也就是120°,左右两个角都是30°,所以这个三角形的内角和是60°+60°+30°+30°=180°。
4.【思维拓展题】下面各图形的内角和分别是多少度?
正确解答:
360° 540°
思路分析:如图,左边的四边形可以分割成2个三角形,所以内角和是180°×2=360°,右边的五边形可以分割成3个三角形,所以内角和是180°×3=540°。
练一练(2)
1.填空。
(1)在直角三角形中,两个锐角的度数和是( )°。
(2)(成都市锦江区)一个三角形的两个角的度数和是85°,这个三角形的第三个角的度数是( )°,这个三角形是( )三角形。
2.它们画的分别是什么三角形?(选题源自《小学教材全练》16页2题)
田田画的是_________________ _;萝萝画的是__________________。
90
95
180
钝角三角形或等腰三角形
锐角三角形
3.(合肥市政务区)下面是两块三角形玻璃打碎后留下的碎片,你知道它们原来各是什么三角形吗?
正确解答:
钝角三角形 锐角三角形或等边三角形
思路分析:因为三角形的内角和是180°,所以可以根据已知角的度数和三角形的内角和求出未知角的度数,从而判断出它们原来各是什么三角形。
4.埃及金字塔的四个侧面的形状都是等腰三角形,每个等腰三角形的顶角约是52°。埃及金字塔每个侧面的底角大约是多少度?
正确解答:
(180°-52°)÷2=64°
答:埃及金字塔每个侧面的底角大约是64°。
思路分析:根据三角形的内角和是180°及等腰三角形的两个底角度数相等,即可求出埃及金字塔每个侧面的底角大约是多少度。
5.刘大爷家有一块直角三角形菜地,在这块直角三角形菜地中,较大锐角的度数是较小锐角的2倍,你知道这块菜地三个角的度数吗?
正确解答:
90°÷(2+1)=30°
30°×2=60°
答:这块菜地三个角的度数分别是30°,60°,90°。
思路分析:可以通过画图来整理题中的数量关系,如下图:
较大锐角和较小锐角的度数和是90°,其中较小锐角占1份,较大锐角占2份,90°÷(2+1)=30°,即较小锐角的度数为30°,则较大锐角的度数为30°×2=60°。
6.【思维拓展题】如下图,等边三角形内有一个等腰三角形,并且∠1=∠2,∠3=∠4,求∠5的度数。
正确解答:
∠5=120°
思路分析:因为大三角形是等边三角形,所以∠1+∠2=∠3+∠4=60°。又因为∠1=∠2,∠3=∠4,所以2∠1=2∠3=60°,∠1=∠3=60°÷2=30°。在等腰三角形中,∠1+∠3=60°,∠5=180°-(∠1+∠3)=180°-60°=120°。
