人教版数学七年级上册同步课件:3.4 第3课时行程问题与一元一次方程(共20张PPT)
文档属性
| 名称 | 人教版数学七年级上册同步课件:3.4 第3课时行程问题与一元一次方程(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 22:17:13 | ||
图片预览




文档简介
(共20张PPT)
第三章 一元一次方程
3.4 第3课时 路程问题与一元一次方程
知识回顾
2.行程问题中常见的量都有什么?
路程 速度 时间
3.行程问题中常见的量之间的数量关系是什么?
1.行程问题常见题型?
相向而行---相遇问题 同向而行---追击问题
情景导入
致100米的运动员:
一声枪响,
你们亮出自己的风采,
在这短短的100米中,
你们与时间争分夺秒,
只为了那最后的冲刺。
不管结果如何,你们都是胜利者。
因为,你们曾与时间竞赛。
在百米比赛中,裁判员会记录运动员所用的时间,你会计算运动员的速度吗?
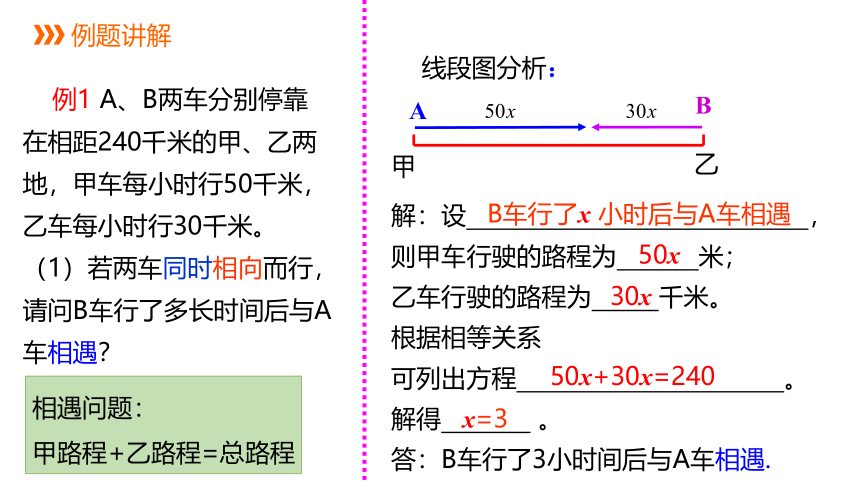
例1 A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(1)若两车同时相向而行,请问B车行了多长时间后与A车相遇?
甲
乙
A
B
线段图分析:
解:设 ,
则甲车行驶的路程为 米;
乙车行驶的路程为 千米。
根据相等关系
可列出方程 。
解得 。
答:B车行了3小时间后与A车相遇.
50x+30x=240
30x
50x
B车行了x 小时后与A车相遇
例题讲解
x=3
相遇问题:
甲路程+乙路程=总路程
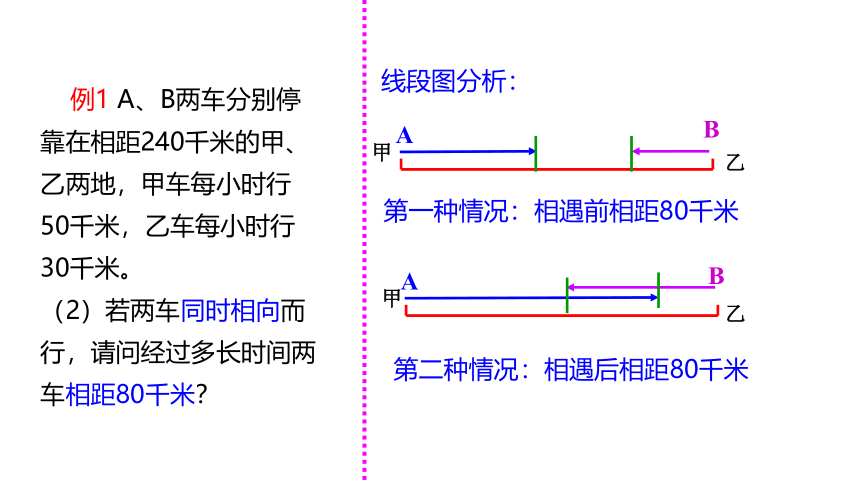
例1 A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(2)若两车同时相向而行,请问经过多长时间两车相距80千米?
线段图分析:
甲
乙
A
B
甲
乙
A
B
第一种情况:相遇前相距80千米
第二种情况:相遇后相距80千米
甲
乙
A
B
80千米
甲
乙
A
B
80千米
50x
30x
30x
50x
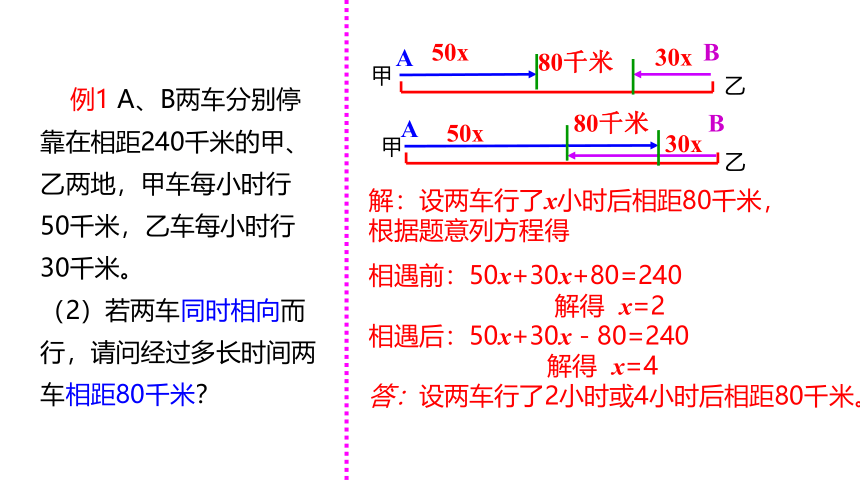
解:设两车行了x小时后相距80千米,
根据题意列方程得
相遇前:50x+30x+80=240
解得 x=2
相遇后:50x+30x - 80=240
解得 x=4
答:设两车行了2小时或4小时后相距80千米。
例1 A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(2)若两车同时相向而行,请问经过多长时间两车相距80千米?
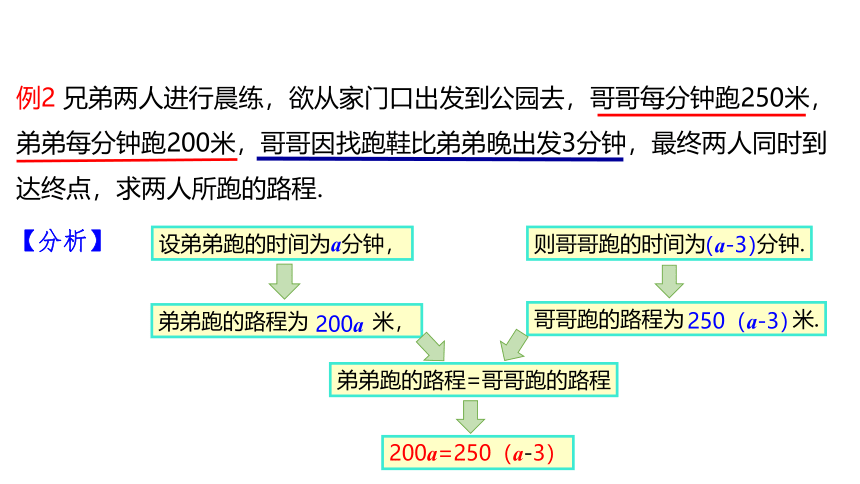
例2 兄弟两人进行晨练,欲从家门口出发到公园去,哥哥每分钟跑250米,弟弟每分钟跑200米,哥哥因找跑鞋比弟弟晚出发3分钟,最终两人同时到达终点,求两人所跑的路程.
设弟弟跑的时间为a分钟,
则哥哥跑的时间为 分钟.
弟弟跑的路程为 米,
哥哥跑的路程为 米.
弟弟跑的路程=哥哥跑的路程
200a=250(a-3)
【分析】
(a-3)
200a
250(a-3)
解:设弟弟跑的时间为a分钟,则哥哥跑的时间为(a-3)分钟.
根据题意列方程,得:
200a=250(a-3)
解得: a=15
所以:15×200=3000(米)
答:两人所跑的路程为3000米.
例2 兄弟两人进行晨练,欲从家门口出发到公园去,哥哥每分钟跑250米,弟弟每分钟跑200米,哥哥因找跑鞋比弟弟晚出发3分钟,最终两人同时到达终点,求两人所跑的路程.
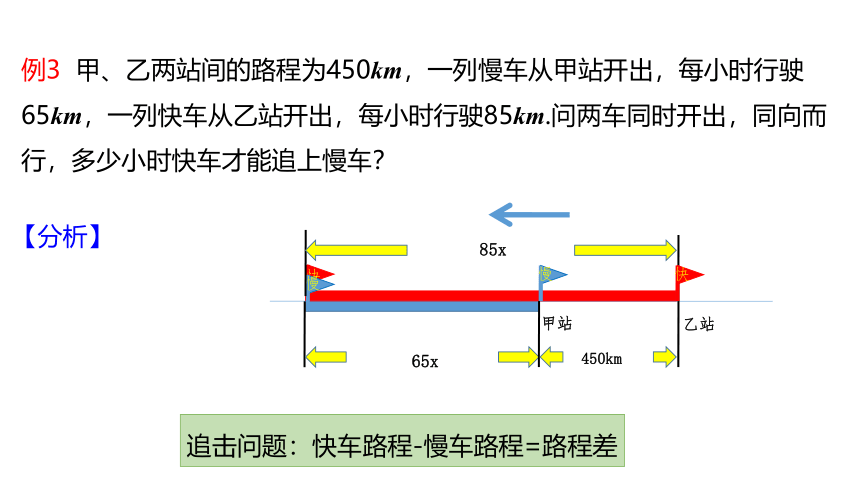
例3 甲、乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km,一列快车从乙站开出,每小时行驶85km.问两车同时开出,同向而行,多少小时快车才能追上慢车?
快
慢
甲站
乙站
450km
慢
快
65x
85x
【分析】
追击问题:快车路程-慢车路程=路程差
例3 甲、乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km,一列快车从乙站开出,每小时行驶85km.问两车同时开出,同向而行,多少小时快车才能追上慢车?
解:设x小时快车才能追上慢车,根据题意列方程,得:
85x-65x=450
解得: x=22.5
答: 22.5小时快车才能追上慢车.
速度(km/h) 时间(h) 路程(km)
顺水
逆水
例4 一船航行于A、B两个码头之间,顺水航行需要2小时,逆水航行需要2.5小时,已知水流速度是3km/h,求这两个码头之间的距离
A码头
B码头
水流方向
x+3
x - 3
2
2.5
2(x+3)
2.5( x- 3)
解:设船在静水中的速度是 x km/h
顺逆问题:
顺水速度=船速+水速
逆水速度=船速-水速
例3 一船航行于A、B两个码头之间,顺水航行需要2小时,逆水航行需要2.5小时,已知水流速度是3km/h,求这两个码头之间的距离
解:设船在静水中的速度是 x km/h,
根据题意得
2(x+3)=2.5(x-3)
解得x=27
2(x+3)=2×(27+3)=60
答:这两个码头之间的距离为60千米.
备注:顺逆问题是实际应用题的难点,主要是因为速度不是单一的量,是两个速度的和或者差.根据顺逆的路程相等列方程.
随堂演练
B
1.一条河的水流速度是1.6km/h,某条船在静水中的速度是akm/h,则该船在这条河中逆流行驶的速度是( )
A.(a+1.6)km/h B.(a﹣1.6)km/h
C.(a+3.2)km/h D.(a﹣3.2)km/h
D
2.从甲地到乙地,公共汽车原需行驶7小时,开通高速公路后,车速平均每小时增加了20千米,只需5个小时即可到达.则公共汽车提速后的速度是( )千米/时.
A. 40 B. 50 C. 60 D. 70
B
3.甲、乙两人同时从相距25千米的A地去B地,甲骑摩托车,乙骑自行车,甲的速度是乙的速度的3倍,甲到达B地后停留了30分钟,然后从B地返回A地,在途中遇见了乙,此时距他们出发的时间刚好是1小时,则甲的速度是( )
A.20千米/小时 B.60千米/小时
C.25千米/小时 D.75千米小时
4.如图,小黄和小陈观察蜗牛爬行,蜗牛在以A为起点沿直线匀速爬向B点的过程中,到达C点时用了6分钟,设还需要x分钟才能到达B点,根据题意列方程为 .
5.一对学生去校外参加劳动,以4千米每时的速度步行前往,走了半小时,学校有紧急通知要传给队长,通讯员骑自行车以14千米每时的速度按原路追上去,通讯员要多少时间才能追上学生队伍?
解:设通讯员要x小时才能追上学生队伍,
根据题意得
4×0.5+4x=14x
解得 x=0.2
答:通讯员要0.2小时才能追上学生队伍
6.两运动员在田径场练习长跑,田径场周长是400米,已知甲每分钟跑200米,乙每分钟跑160米,两人同时 从同一地点出发,同向而行,经过 多少分钟两人才能第一次相遇?
解:设两个运动员第一次相遇所需要时间为x分钟。
根据题意得
200x-160x=400
解得 x=10
答:经过 10分钟两人才能第一次相遇.
7.一架飞机在两城之间航行,风速为24 km/h,顺风飞行要2小时50分,逆风飞行要3小时,求两城距离.
解:设飞机在无风时的速度为x km/h,则在顺风中的速度为(x+24) km/h ,在逆风中的速度为(x-24)km/h.
根据题意,得 .
解得 x=840.
两城市的距离为3×(840-24)=2448 (km).
答:两城市之间的距离为2448 km.
课堂小结
行程问题
相遇问题:甲路程+乙路程=总路程
追击问题:快车路程-慢车路程=路程差
顺逆问题:
逆水速度=船速-水速
环形跑道问题:快的路程-慢的路程=1圈(第1次相遇)
顺水速度=船速+水速
第三章 一元一次方程
3.4 第3课时 路程问题与一元一次方程
知识回顾
2.行程问题中常见的量都有什么?
路程 速度 时间
3.行程问题中常见的量之间的数量关系是什么?
1.行程问题常见题型?
相向而行---相遇问题 同向而行---追击问题
情景导入
致100米的运动员:
一声枪响,
你们亮出自己的风采,
在这短短的100米中,
你们与时间争分夺秒,
只为了那最后的冲刺。
不管结果如何,你们都是胜利者。
因为,你们曾与时间竞赛。
在百米比赛中,裁判员会记录运动员所用的时间,你会计算运动员的速度吗?
例1 A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(1)若两车同时相向而行,请问B车行了多长时间后与A车相遇?
甲
乙
A
B
线段图分析:
解:设 ,
则甲车行驶的路程为 米;
乙车行驶的路程为 千米。
根据相等关系
可列出方程 。
解得 。
答:B车行了3小时间后与A车相遇.
50x+30x=240
30x
50x
B车行了x 小时后与A车相遇
例题讲解
x=3
相遇问题:
甲路程+乙路程=总路程
例1 A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(2)若两车同时相向而行,请问经过多长时间两车相距80千米?
线段图分析:
甲
乙
A
B
甲
乙
A
B
第一种情况:相遇前相距80千米
第二种情况:相遇后相距80千米
甲
乙
A
B
80千米
甲
乙
A
B
80千米
50x
30x
30x
50x
解:设两车行了x小时后相距80千米,
根据题意列方程得
相遇前:50x+30x+80=240
解得 x=2
相遇后:50x+30x - 80=240
解得 x=4
答:设两车行了2小时或4小时后相距80千米。
例1 A、B两车分别停靠在相距240千米的甲、乙两地,甲车每小时行50千米,乙车每小时行30千米。
(2)若两车同时相向而行,请问经过多长时间两车相距80千米?
例2 兄弟两人进行晨练,欲从家门口出发到公园去,哥哥每分钟跑250米,弟弟每分钟跑200米,哥哥因找跑鞋比弟弟晚出发3分钟,最终两人同时到达终点,求两人所跑的路程.
设弟弟跑的时间为a分钟,
则哥哥跑的时间为 分钟.
弟弟跑的路程为 米,
哥哥跑的路程为 米.
弟弟跑的路程=哥哥跑的路程
200a=250(a-3)
【分析】
(a-3)
200a
250(a-3)
解:设弟弟跑的时间为a分钟,则哥哥跑的时间为(a-3)分钟.
根据题意列方程,得:
200a=250(a-3)
解得: a=15
所以:15×200=3000(米)
答:两人所跑的路程为3000米.
例2 兄弟两人进行晨练,欲从家门口出发到公园去,哥哥每分钟跑250米,弟弟每分钟跑200米,哥哥因找跑鞋比弟弟晚出发3分钟,最终两人同时到达终点,求两人所跑的路程.
例3 甲、乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km,一列快车从乙站开出,每小时行驶85km.问两车同时开出,同向而行,多少小时快车才能追上慢车?
快
慢
甲站
乙站
450km
慢
快
65x
85x
【分析】
追击问题:快车路程-慢车路程=路程差
例3 甲、乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km,一列快车从乙站开出,每小时行驶85km.问两车同时开出,同向而行,多少小时快车才能追上慢车?
解:设x小时快车才能追上慢车,根据题意列方程,得:
85x-65x=450
解得: x=22.5
答: 22.5小时快车才能追上慢车.
速度(km/h) 时间(h) 路程(km)
顺水
逆水
例4 一船航行于A、B两个码头之间,顺水航行需要2小时,逆水航行需要2.5小时,已知水流速度是3km/h,求这两个码头之间的距离
A码头
B码头
水流方向
x+3
x - 3
2
2.5
2(x+3)
2.5( x- 3)
解:设船在静水中的速度是 x km/h
顺逆问题:
顺水速度=船速+水速
逆水速度=船速-水速
例3 一船航行于A、B两个码头之间,顺水航行需要2小时,逆水航行需要2.5小时,已知水流速度是3km/h,求这两个码头之间的距离
解:设船在静水中的速度是 x km/h,
根据题意得
2(x+3)=2.5(x-3)
解得x=27
2(x+3)=2×(27+3)=60
答:这两个码头之间的距离为60千米.
备注:顺逆问题是实际应用题的难点,主要是因为速度不是单一的量,是两个速度的和或者差.根据顺逆的路程相等列方程.
随堂演练
B
1.一条河的水流速度是1.6km/h,某条船在静水中的速度是akm/h,则该船在这条河中逆流行驶的速度是( )
A.(a+1.6)km/h B.(a﹣1.6)km/h
C.(a+3.2)km/h D.(a﹣3.2)km/h
D
2.从甲地到乙地,公共汽车原需行驶7小时,开通高速公路后,车速平均每小时增加了20千米,只需5个小时即可到达.则公共汽车提速后的速度是( )千米/时.
A. 40 B. 50 C. 60 D. 70
B
3.甲、乙两人同时从相距25千米的A地去B地,甲骑摩托车,乙骑自行车,甲的速度是乙的速度的3倍,甲到达B地后停留了30分钟,然后从B地返回A地,在途中遇见了乙,此时距他们出发的时间刚好是1小时,则甲的速度是( )
A.20千米/小时 B.60千米/小时
C.25千米/小时 D.75千米小时
4.如图,小黄和小陈观察蜗牛爬行,蜗牛在以A为起点沿直线匀速爬向B点的过程中,到达C点时用了6分钟,设还需要x分钟才能到达B点,根据题意列方程为 .
5.一对学生去校外参加劳动,以4千米每时的速度步行前往,走了半小时,学校有紧急通知要传给队长,通讯员骑自行车以14千米每时的速度按原路追上去,通讯员要多少时间才能追上学生队伍?
解:设通讯员要x小时才能追上学生队伍,
根据题意得
4×0.5+4x=14x
解得 x=0.2
答:通讯员要0.2小时才能追上学生队伍
6.两运动员在田径场练习长跑,田径场周长是400米,已知甲每分钟跑200米,乙每分钟跑160米,两人同时 从同一地点出发,同向而行,经过 多少分钟两人才能第一次相遇?
解:设两个运动员第一次相遇所需要时间为x分钟。
根据题意得
200x-160x=400
解得 x=10
答:经过 10分钟两人才能第一次相遇.
7.一架飞机在两城之间航行,风速为24 km/h,顺风飞行要2小时50分,逆风飞行要3小时,求两城距离.
解:设飞机在无风时的速度为x km/h,则在顺风中的速度为(x+24) km/h ,在逆风中的速度为(x-24)km/h.
根据题意,得 .
解得 x=840.
两城市的距离为3×(840-24)=2448 (km).
答:两城市之间的距离为2448 km.
课堂小结
行程问题
相遇问题:甲路程+乙路程=总路程
追击问题:快车路程-慢车路程=路程差
顺逆问题:
逆水速度=船速-水速
环形跑道问题:快的路程-慢的路程=1圈(第1次相遇)
顺水速度=船速+水速
