直线与椭圆的位置关系
图片预览





文档简介
课件18张PPT。直线与椭圆的位置关系
1.掌握椭圆的几何性质,掌握用坐标法研究直线与椭圆的位置关系,熟练地求弦长、面积、对称等问题.
2.培养数学理解能力及分析问题解决问题的能力.
教学目标
1、重点:掌握由曲线方程确定曲线位置关系的主要方法:判别式法;
掌握由位置关系求曲线的方法:基本量法。
2.难点:由于直线与圆锥曲线的关系,往往转化为方程来解决,但因为直线与圆锥的曲线有一个公共点并不是只是△=0的情况,学生容易出错。因此这是本节课的一个难点。而代数与几何的联系,以及知识的综合应用也本节课的一个难点。
教学重难点1、椭圆的定义?
2、椭圆的几何性质?
3、怎样才能判断直线与椭圆的位置关系?
方法一:几何法
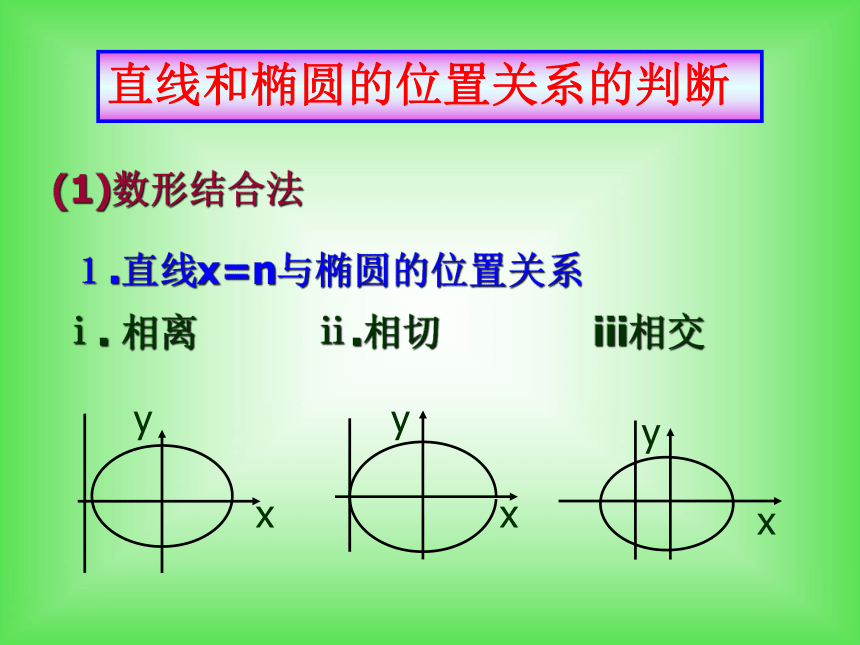
方法二:代数法问题: 1.直线x=n与椭圆的位置关系
ⅰ. 相离 ⅱ.相切 iii相交(1)数形结合法直线和椭圆的位置关系的判断 2.直线y=m与椭圆的位置关系种类:
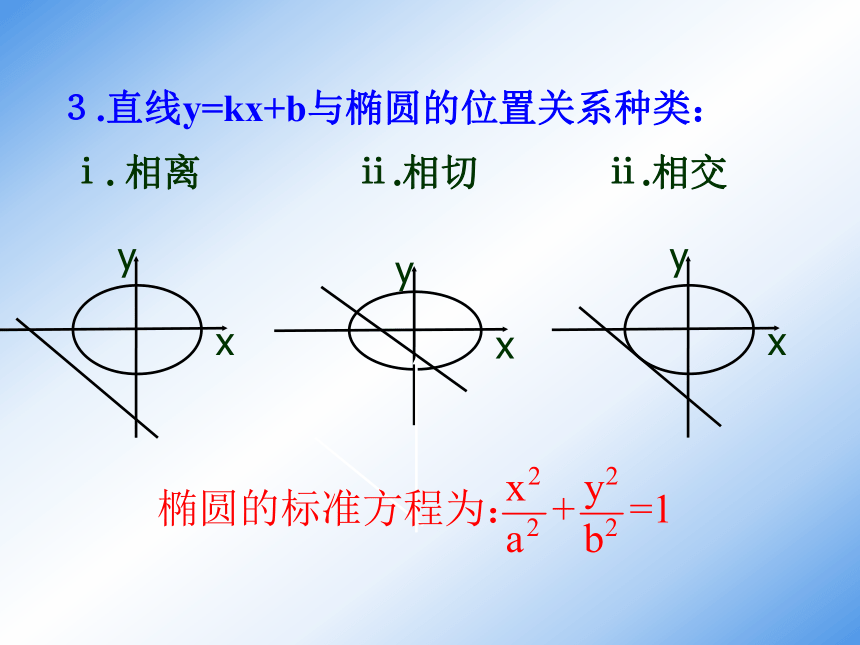
ⅰ. 相离 ⅱ.相切 ⅱ.相交 3.直线y=kx+b与椭圆的位置关系种类:
ⅰ. 相离 ⅱ.相切 ⅱ.相交(2)判别式法 要具体判断出直线和圆的关系,
应该将两个方程式联立.3.直线的斜率为k,被圆锥曲线截得弦AB两端点坐标为(x1, y1 )、(x2, y2),则有弦长公式:?
?
?
?
?
?
例一已知椭圆 及直线 .
(1)当直线和椭圆有公共点时,求实数 的取值范围;
(2)求椭圆截得的最长弦所在的直线方程.
分析:用方程组解的情况来判断,从方程角度看,主要是由一元二次方程根的判别式
解?1)解方程组
消 去整理得
,例题应用(1)
(2)由伟达定理得 ,
弦长 ,
当 时,L取得最大值为,此时直线方程为
. 例2.中心在原点一个焦点为 的椭圆的截直线 所得弦的中点横坐标为 ,求椭圆的方程. 分析:根据题意可设椭圆的标准方程,与直线方程连里解方程组,利用中点公式求得弦的中点的横坐标,最后解关于 的方程组即可. 解:设所求椭圆的方程为
由 得 ①
把直线方程代入椭圆方程,整理得
设弦的两个端点为 , ,则由根与系数的关系得
又中点的横坐标为 .由此得
解①、②得: [分析]本题和例2有相似之处,可仿其解法进行。由于本题的实质是求出直线的斜率,在所给的条件下求直线的斜率的方法较多,故本题的解法较多。 例4已知椭圆 与直线
相交于 两点, 是的 中
点.若 , 斜率为 (O为原点),
求椭圆方程.
分析:本例是一道综合性比较强的问题,求解
本题要利用中点公式求出点坐标,从而得的斜
率,另外还要用到弦长公式:解:由方程组消去 整理得:即:②①解①②得所求的椭圆方程为谢谢指导
1.掌握椭圆的几何性质,掌握用坐标法研究直线与椭圆的位置关系,熟练地求弦长、面积、对称等问题.
2.培养数学理解能力及分析问题解决问题的能力.
教学目标
1、重点:掌握由曲线方程确定曲线位置关系的主要方法:判别式法;
掌握由位置关系求曲线的方法:基本量法。
2.难点:由于直线与圆锥曲线的关系,往往转化为方程来解决,但因为直线与圆锥的曲线有一个公共点并不是只是△=0的情况,学生容易出错。因此这是本节课的一个难点。而代数与几何的联系,以及知识的综合应用也本节课的一个难点。
教学重难点1、椭圆的定义?
2、椭圆的几何性质?
3、怎样才能判断直线与椭圆的位置关系?
方法一:几何法
方法二:代数法问题: 1.直线x=n与椭圆的位置关系
ⅰ. 相离 ⅱ.相切 iii相交(1)数形结合法直线和椭圆的位置关系的判断 2.直线y=m与椭圆的位置关系种类:
ⅰ. 相离 ⅱ.相切 ⅱ.相交 3.直线y=kx+b与椭圆的位置关系种类:
ⅰ. 相离 ⅱ.相切 ⅱ.相交(2)判别式法 要具体判断出直线和圆的关系,
应该将两个方程式联立.3.直线的斜率为k,被圆锥曲线截得弦AB两端点坐标为(x1, y1 )、(x2, y2),则有弦长公式:?
?
?
?
?
?
例一已知椭圆 及直线 .
(1)当直线和椭圆有公共点时,求实数 的取值范围;
(2)求椭圆截得的最长弦所在的直线方程.
分析:用方程组解的情况来判断,从方程角度看,主要是由一元二次方程根的判别式
解?1)解方程组
消 去整理得
,例题应用(1)
(2)由伟达定理得 ,
弦长 ,
当 时,L取得最大值为,此时直线方程为
. 例2.中心在原点一个焦点为 的椭圆的截直线 所得弦的中点横坐标为 ,求椭圆的方程. 分析:根据题意可设椭圆的标准方程,与直线方程连里解方程组,利用中点公式求得弦的中点的横坐标,最后解关于 的方程组即可. 解:设所求椭圆的方程为
由 得 ①
把直线方程代入椭圆方程,整理得
设弦的两个端点为 , ,则由根与系数的关系得
又中点的横坐标为 .由此得
解①、②得: [分析]本题和例2有相似之处,可仿其解法进行。由于本题的实质是求出直线的斜率,在所给的条件下求直线的斜率的方法较多,故本题的解法较多。 例4已知椭圆 与直线
相交于 两点, 是的 中
点.若 , 斜率为 (O为原点),
求椭圆方程.
分析:本例是一道综合性比较强的问题,求解
本题要利用中点公式求出点坐标,从而得的斜
率,另外还要用到弦长公式:解:由方程组消去 整理得:即:②①解①②得所求的椭圆方程为谢谢指导
