必修第二册9.2用样本估计总体 同步练习(Word版含解析)
文档属性
| 名称 | 必修第二册9.2用样本估计总体 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 839.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 00:00:00 | ||
图片预览



文档简介
人教A版(2019)必修第二册 9.2 用样本估计总体 同步练习
一、单选题
1.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是
A.中位数 B.平均数
C.方差 D.极差
2.某台机床加工的产品中次品数的频率分布如表:
次品数 0 1 2 3 4
频率 0.5 0.2 0.05 0.2 0.05
则次品数的平均数为( )A.1.1 B.3 C.1.5 D.2
3.甲 乙 丙 丁四位同学组成的数学学习小组进行了一次小组竞赛,共测试了5道题,每位同学各题得分情况如下表:
题目 学生 第1题 第2题 第3题 第4题 第5题
甲 10 10 10 20 0
乙 10 10 5 15 10
丙 10 10 15 15 10
丁 0 10 10 20 20
下列说法正确的是( )A.甲的平均得分比丙的平均得分高
B.乙的得分极差比丁的得分极差大
C.对于这4位同学,因为第4题的平均得分比第2题的平均得分高,所以第4题相关知识一定比第2题相关知识掌握好
D.对于这4位同学,第3题得分的方差比第5题得分的方差小
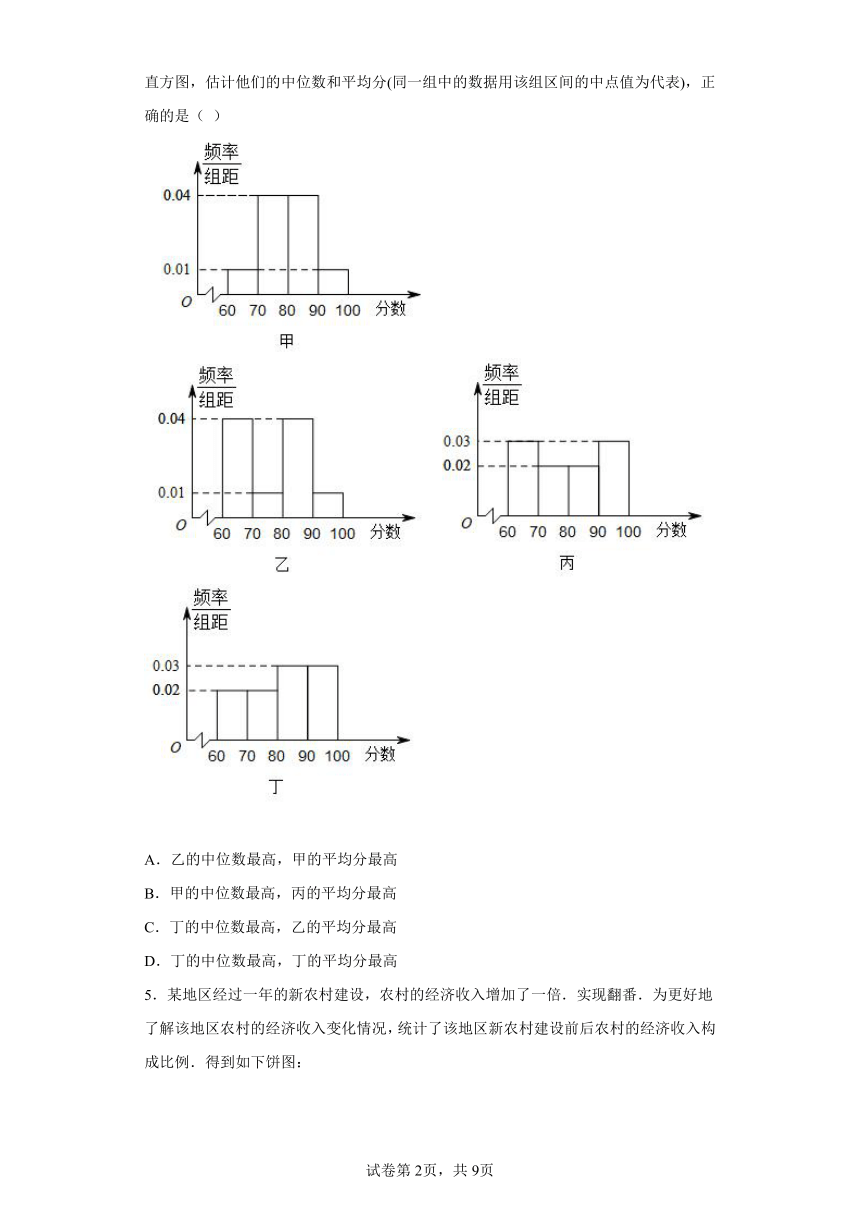
4.甲 乙 丙 丁四位同学在高中学业水平模拟测试中的成绩分布分别为下面的频率分布直方图,估计他们的中位数和平均分(同一组中的数据用该组区间的中点值为代表),正确的是( )
A.乙的中位数最高,甲的平均分最高
B.甲的中位数最高,丙的平均分最高
C.丁的中位数最高,乙的平均分最高
D.丁的中位数最高,丁的平均分最高
5.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:
则下面结论中不正确的是
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
6.某高中为了解学生课外知识的积累情况,随机抽取名同学参加课外知识测试,测试共道题,每答对一题得分,答错得分.已知每名同学至少能答对道题,得分不少于分记为及格,不少于分记为优秀,测试成绩百分比分布图如图所示,则下列说法正确的是( )
A.该次课外知识测试及格率为
B.该次课外知识测试得满分的同学有名
C.该次测试成绩的中位数大于测试成绩的平均数
D.若该校共有名学生,则课外知识测试成绩能得优秀的同学大约有名
7.已知甲 乙 丙 丁 戊五位同学高一入学时年龄的平均数 中位数均为16,方差为0.8,则三年后,下列判断错误的是( )
A.这五位同学年龄的平均数变为19 B.这五位同学年龄的中位数变为19
C.这五位同学年龄的方差仍为0.8 D.这五位同学年龄的方差变为3.8
8.有13名同学参加百米竞赛,预赛成绩各不相同,要取前6名参加决赛,小明同学已经知道了自己的成绩,为了判断自己是否能进入决赛,他还需要知道13名同学成绩的( )
A.平均数 B.众数 C.中位数 D.方差
9.若样本数据,,…,的标准差为,则数据,,…,的标准差为( )
A. B. C. D.
10.某赛季甲乙两名篮球运动员在若干场比赛中的得分情况如下:
甲:21、22、23、25、28、29、30、30;
乙:14、16、23、26、28、30、33、38.
则下列描述合理的是( )
A.甲队员每场比赛得分的平均值大 B.乙队员每场比赛得分的平均值大
C.甲队员比赛成绩比较稳定 D.乙队员比赛成绩比较稳定
11.2020年宿州市某中学参加高中数学建模(应用)能力测试,高一年级有60人,高二年级有40人.高一的平均成绩为70分,高二的平均成绩为80分,则参加测试的100名学生的平均成绩为( )
A.72分 B.73分 C.74分 D.75分
12.已知甲 乙两组数据(已按从小到大的顺序排列):甲组:27,28,39,40,m,50;乙组:24,n,34,43,48,52.若这两组数据的30百分位数 80百分位数分别相等,则等于( )
A. B. C. D.
13.某学校组建了演讲,舞蹈 航模 合唱,机器人五个社团,全校名学生每人都参加且只参加其中一个社团,校团委从这名学生中随机选取部分学生进行调查,并将调查结果绘制了如下不完整的两个统计图:
则选取的学生中参加机器人社团的学生数为( )
A. B. C. D.
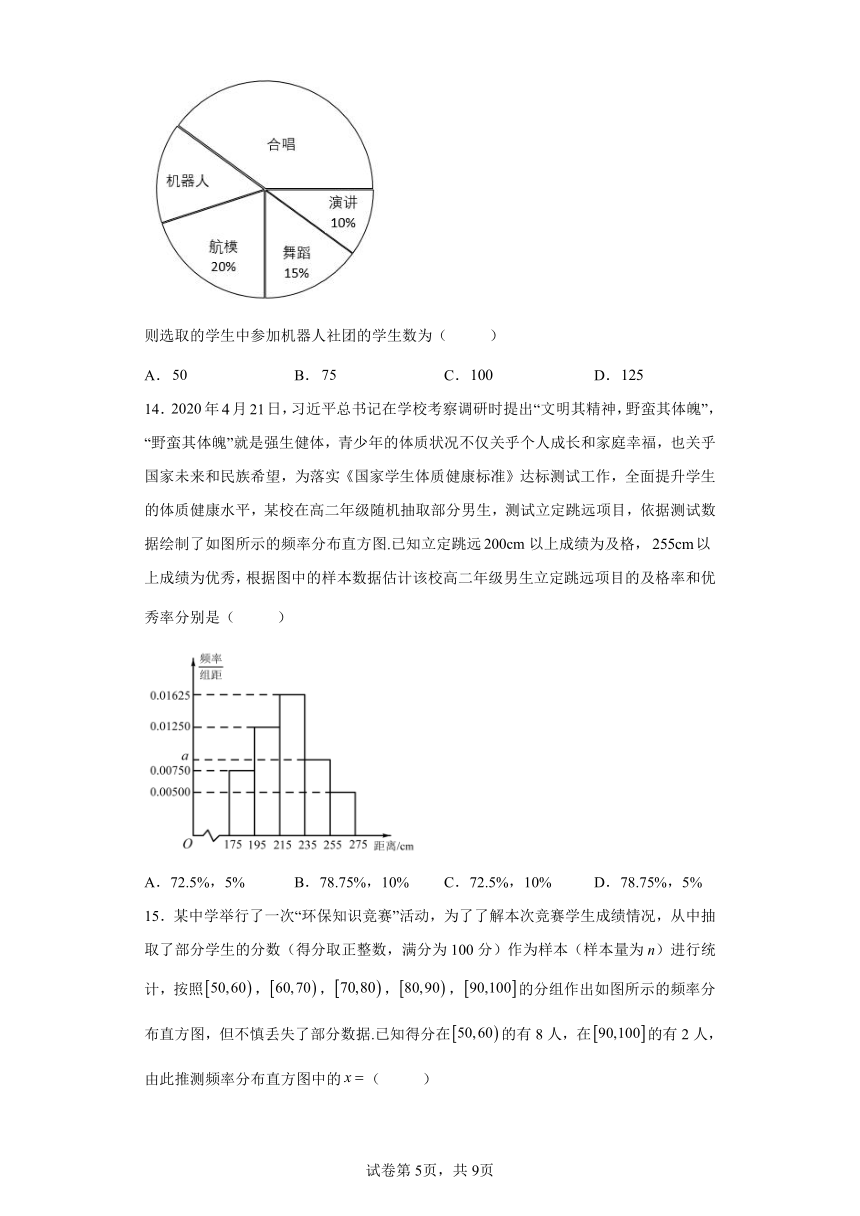
14.年月日,习近平总书记在学校考察调研时提出“文明其精神,野蛮其体魄”,“野蛮其体魄”就是强生健体,青少年的体质状况不仅关乎个人成长和家庭幸福,也关乎国家未来和民族希望,为落实《国家学生体质健康标准》达标测试工作,全面提升学生的体质健康水平,某校在高二年级随机抽取部分男生,测试立定跳远项目,依据测试数据绘制了如图所示的频率分布直方图.已知立定跳远以上成绩为及格,以上成绩为优秀,根据图中的样本数据估计该校高二年级男生立定跳远项目的及格率和优秀率分别是( )
A.72.5%,5% B.78.75%,10% C.72.5%,10% D.78.75%,5%
15.某中学举行了一次“环保知识竞赛”活动,为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本量为n)进行统计,按照,,,,的分组作出如图所示的频率分布直方图,但不慎丢失了部分数据.已知得分在的有8人,在的有2人,由此推测频率分布直方图中的( )
A.0.04 B.0.03 C.0.02 D.0.01
二、填空题
16.一个容量为100的样本,其数据的分组与各组的频数如下表:
组别 [0,10) [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]
频数 12 13 24 15 16 13 7
则样本数据落在[10,40)上的频率为________.
17.已知某样本数据分别为1,4,3,a,6,且样本均值,则样本方差_________.
18.已知一组数据,,3,5的中位数为7,平均数为8,则______.
三、解答题
19.某公司为了解用户对其产品的满意程度,采用分层抽样的方法从A,B两个地区共抽取了500名用户,请用户根据满意程度对该公司品评分,该公司将收集到的数据按照,,,分组,绘制成评分频率分布直方图如下:
已知A地区用户约为40000人,B地区用户约为10000人.
(1)求该公司采用分层抽样的方法从A,B两个地区分别抽取的用户人数;
(2)根据频率分布直分图,估计B地区所有用户中,对该产品评分不低于80分的用户的人数;
(3)根据频率分布直方图,估计A地区抽取的400名用户对该公司产品的评分的平均值为,B地区抽取的100名用户对该公司产品的评分的平均值为,以及A,B两个地区抽取的500名用户对该公司产品的评分的平均值为,试比较和的大小.(结论不要求证明)
20.鱼卷是泉州十大名小吃之一,不但本地人喜欢,而且深受外来游客的赞赏.小张从事鱼卷生产和批发多年,有着不少来自零售商和酒店的客户当地的习俗是农历正月不生产鱼卷,客户正月所需要的鱼卷都会在上一年农历十二月底进行一次性采购小张把去年年底采购鱼卷的数量x(单位:箱)在的客户称为“熟客”,并把他们去年采购的数量制成下表:
采购数x
客户数 10 10 5 20 5
(1)根据表中的数据作出频率分布直方图,并估计采购数在168箱以上(含168箱)的“熟客”人数;
(2)若去年年底“熟客”们采购的鱼卷数量占小张去年年底总的销售量的,估算小张去年年底总的销售量(同一组中的数据用该组区间的中点值为代表);
(3)由于鱼卷受到游客们的青睐,小张做了一份市场调查,决定今年年底是否在网上出售鱼卷,若不在网上出售鱼卷,则按去年的价格出售,每箱利润为20元,预计销售量与去年持平;若在网上出售鱼卷,则需把每箱售价下调2至5元,且每下调m元()销售量可增加1000m箱,求小张今年年底收入Y(单位:元)的最大值.
21.某校根据该校高一年级100名学生的英语成绩(不包括听力部分)得到如下频数分布表:
分组
频数 8 24 36 28 4
(1)根据频数分布表,作出这些数据的频率分布直方图,并求这100名学生英语成绩(不包括听力部分)的平均分(同一组中的数据用该组区间的中间值作代表);
(2)若这100名学生英语成绩的优秀率为,求英语成绩为优秀的分数线(保留整数位).
22.生产过程中,测得纤维产品的纤度(表示纤细的一种量),共有100个数据,将数据分组如下表:
分组 频数 频率
4
25
30
29
10
2
合计 100
(1)完成频率分布表,并画出频率分布直方图;
(2)估计纤度落在内的可能性及纤度小于的可能性各是多少?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
可不用动笔,直接得到答案,亦可采用特殊数据,特值法筛选答案.
【详解】
设9位评委评分按从小到大排列为.
则①原始中位数为,去掉最低分,最高分,后剩余,
中位数仍为,A正确.
②原始平均数,后来平均数
平均数受极端值影响较大,与不一定相同,B不正确
③
由②易知,C不正确.
④原极差,后来极差可能相等可能变小,D不正确.
本题旨在考查学生对中位数、平均数、方差、极差本质的理解.
2.A
平均数是次品数与相应的频率乘积之和.
【详解】
设数据xi出现的频率为pi(i=1,2,…,n),则x1,x2,…,xn的平均数为
x1p1+x2p2+…+xnpn=0×0.5+1×0.2+2×0.05+3×0.2+4×0.05=1.1.
故选:A
3.D
根据题意计算对应平均值、极差和方差,进行比较,逐一判断选项正误即可.
【详解】
选项A中,甲的平均分为,丙的平均分为,故甲的平均得分比丙的平均得分低,故错误;
选项B中,乙的得分极差为,丁的得分极差为,极差相等,故错误;
选项C中,不清楚两题的具体分值是否相同,所以不能通过平均分判断第4题相关知识一定比第2题相关知识掌握好,故错误;
选项D中,第3题得分的平均值为,
故方差为,
第5题得分的平均分为,
故方差为,
故第3题得分的方差比第5题得分的方差小.故正确.
故选:D.
4.D
由频率分布直方图易得四位同学的中位数,可比较出大小,再分别计算出平均数进行比较,可得选项.
【详解】
甲 乙 丙三位同学的成绩中位数都是80,丁的成绩中位数大于80;
甲的平均成绩为,
乙的平均成绩为,
丙的平均成绩为,
丁的平均成绩为
故选:D.
5.A
首先设出新农村建设前的经济收入为M,根据题意,得到新农村建设后的经济收入为2M,之后从图中各项收入所占的比例,得到其对应的收入是多少,从而可以比较其大小,并且得到其相应的关系,从而得出正确的选项.
【详解】
设新农村建设前的收入为M,而新农村建设后的收入为2M,
则新农村建设前种植收入为0.6M,而新农村建设后的种植收入为0.74M,所以种植收入增加了,所以A项不正确;
新农村建设前其他收入我0.04M,新农村建设后其他收入为0.1M,故增加了一倍以上,所以B项正确;
新农村建设前,养殖收入为0.3M,新农村建设后为0.6M,所以增加了一倍,所以C项正确;
新农村建设后,养殖收入与第三产业收入的综合占经济收入的,所以超过了经济收入的一半,所以D正确;
故选A.
点睛:该题考查的是有关新农村建设前后的经济收入的构成比例的饼形图,要会从图中读出相应的信息即可得结果.
6.C
由百分比图知,成绩为100分、80分、60分、40分的百分比分别为,结合各项的描述即可判断其正误.
【详解】
由图知,及格率为,故A错误.
该测试满分同学的百分比为,即有名,B错误.
由图知,中位数为分,平均数为分,故C正确.
由题意,名学生成绩能得优秀的同学有,故D错误.
故选:C
7.D
利用平均数、中位数、方差的定义直接求解.
【详解】
甲、乙、丙、丁、戊五位同学高一入学时年龄的平均数、中位数均为16,方差位0.8,
三年后,
这五位同学年龄的平均数变为16+3=19,故A正确;
这五位同学年龄的中位数变为16+3=19,故B正确;
这五位同学的方差不变,仍为0.8,故C正确,D错误.
故选:D.
8.C
成绩由小到大排列,能否进入决赛就看小明成绩排名是否在第7以前即可得解.
【详解】
把13名同学成绩按由大到小排列,取成绩靠前的6个成绩进入决赛,即最中间一个数之前的6个成绩进入决赛,
13个成绩按由大到小排列时,最中间一个数即是中位数.
故选:C
9.B
首先设原数据的平均数为,则新数据的平均数为,然后结合原数据的方差,利用方差的公式计算得出新数据的方差,再求出标准差即可.
【详解】
设原数据的平均数为,则新数据的平均数为,
则原数据的方差为,
则新数据的方差为:
.
故数据,,…,的标准差为:8.
故选:B.
10.C
计算均值,再根据数据的集中度判断.
【详解】
甲的均值为,
乙的均值为,
两者均值相同,甲的方差为
乙的方差为
,
甲的方差小于乙的方差,甲稳定.
故选:C.
11.C
根据平均值的计算公式,由题中条件直接计算,即可得出结果.
【详解】
由题意可得,参加测试的100名学生的平均成绩为.
故选:C.
12.A
根据百分位数的定义并结合已知条件求出的值,由此可得的值.
【详解】
因为×6=1.8,×6=4.8,所以30百分位数为第二个数,即n=28,80百分位数为第五个数即m=48,所以==.
故选:A
13.B
根据演讲的人数,求得本次调查的人数为人,进而求得机器人所占的比例,即可求解.
【详解】
由题意,本次调查的人数为人,
其中合唱比赛所占的比例为,
所以机器人所占的比例为,
所以选取的学生中参加机器人社团的学生数为人.
故选:B.
14.B
计算以上的矩形的面积之和,可得出该校高二年级男生立定跳远项目的及格率,计算以上的矩形的面积之和,可得出该校高二年级男生立定跳远项目的优秀率.
【详解】
由题意可知,该校高二年级男生立定跳远项目的及格率为,
该校高二年级男生立定跳远项目的优秀率为.
故选:B.
15.B
根据频率分布直方图,先求得抽取学生的人数.
【详解】
得分在的有8人, 得分在的频率为
所以抽取中的人数为人
在的有2人,所以在的频率为,所以
∴由频率分布直方图各小矩形面积和为1,得.
解得.
故选:B.
本题考查了频率分布直方图的意义,补全频率分布直方图,属于基础题.
16.0.52
根据图表,样本数据落在[10,40)上的频数为13+24+15=52,根据频率公式即可得解.
【详解】
样本数据落在[10,40)上的频数为13+24+15=52.
则样本数据落在[10,40)上的频率为=0.52.
故答案为:0.52
17.##
先求得的值,然后求得样本方差.
【详解】
依题意,
所以.
故答案为:
18.135
先由平均数为8,求出,然后分和讨论,当时,不妨设,再分,和三种情况讨论即可
【详解】
因为一组数据,,3,5的平均数为8,
所以,解得,
若,则,此时四个数为,显然中位数不是7,
不妨设,若,则,此时4个数排列为,中位数为4,不合题意,
若时,则,此时4个数排列为,显然中位数不是7,
若,则4个数排列为,则中位数为,解得,则,
所以,
故答案为:135
19.(1)地区抽取400户,地区抽取100户;(2)10;(3)当时,,时,,时,.
(1)根据分层抽样,样本比等于总体比求得抽取的用户人数;
(2)由频率分布图得出频率后可得所求人数;
(3)根据均值的定义求出,作差比较.
【详解】
(1)设A,B两个地区抽取的用户人数分别为,则,所以,;
(2)由频率分布图知,B地区所有用户中,对该产品评分不低于80分的用户频率为,人数;
(3)由题意,
,
所以当时,,时,,时,.
20.(1)见解析 17人(2)12000箱 (3)最大值为256000元.
(1)根据统计表作出频率分布直方图,再根据直方图即可求出,
(2)根据统计表和直方图即可求出,
(3)没有在网上出售鱼卷,则今年的年底小张的收入为(元,若网上出售鱼卷,则今年的年底的销售量为,即可求出的最大值,比较即可
【详解】
解: (1)作出频率分布直方图,如图
根据上图,可知采购量在168箱以上(含168箱)的“熟客”人数为
(2)去年年底“熟客”所采购的鱼卷总数大约为
(箱)
小张去年年底总的销售量为(箱)
(3)若不在网上出售鱼卷,则今年年底小张的收入为(元);
若在网上出售鱼卷,则今年年底的销售量为箱,每箱的利润为,
则今年年底小张的收入为
,
当时, 取得最大值256000
∵,
∴小张今年年底收入的最大值为256000元.
本题考查了频率分布直方图的计算问题,属于基础题.
21.(1)频率分布直方图答案见解析,平均分;(2)分数线为99.
(1)作出频率分布直方图,结合频率分布直方图的性质能求出平均分.(2)由题可知,,的频率为0.04,,的频率为0.28,由此能求出英语成绩为优秀的分数线.
【详解】
解:(1)频率分布直方图如下:
平均分.
(2)由题可知,的频率为0.04,
的频率为0.28,
因为这100名学生英语成绩的优秀率为,所以成绩优秀的分数线在之间,
设优秀成绩的分数线为x,则有.1
解得.
故英语成绩为优秀的分数线为99.
22.(1)答案见解析;(2),.
(1)根据题意,由频率与频数的关系,计算可得各组的频率,进而可以做出频率分布表,结合分布表,进而可以做出频率分步直方图;
(2)由频率分布表可得纤度落在中的可能性,并可计算纤度小于的可能性.
【详解】
频率分布表如下:
分组 频数 频率
4
25
30
29
10
合计
频率分布直方图如图所示.
(2)利用样本估计总体,则纤度落在的可能性即为纤度落在的频率,即为.
纤度小于的可能性即为纤度小于的频率,即为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是
A.中位数 B.平均数
C.方差 D.极差
2.某台机床加工的产品中次品数的频率分布如表:
次品数 0 1 2 3 4
频率 0.5 0.2 0.05 0.2 0.05
则次品数的平均数为( )A.1.1 B.3 C.1.5 D.2
3.甲 乙 丙 丁四位同学组成的数学学习小组进行了一次小组竞赛,共测试了5道题,每位同学各题得分情况如下表:
题目 学生 第1题 第2题 第3题 第4题 第5题
甲 10 10 10 20 0
乙 10 10 5 15 10
丙 10 10 15 15 10
丁 0 10 10 20 20
下列说法正确的是( )A.甲的平均得分比丙的平均得分高
B.乙的得分极差比丁的得分极差大
C.对于这4位同学,因为第4题的平均得分比第2题的平均得分高,所以第4题相关知识一定比第2题相关知识掌握好
D.对于这4位同学,第3题得分的方差比第5题得分的方差小
4.甲 乙 丙 丁四位同学在高中学业水平模拟测试中的成绩分布分别为下面的频率分布直方图,估计他们的中位数和平均分(同一组中的数据用该组区间的中点值为代表),正确的是( )
A.乙的中位数最高,甲的平均分最高
B.甲的中位数最高,丙的平均分最高
C.丁的中位数最高,乙的平均分最高
D.丁的中位数最高,丁的平均分最高
5.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:
则下面结论中不正确的是
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
6.某高中为了解学生课外知识的积累情况,随机抽取名同学参加课外知识测试,测试共道题,每答对一题得分,答错得分.已知每名同学至少能答对道题,得分不少于分记为及格,不少于分记为优秀,测试成绩百分比分布图如图所示,则下列说法正确的是( )
A.该次课外知识测试及格率为
B.该次课外知识测试得满分的同学有名
C.该次测试成绩的中位数大于测试成绩的平均数
D.若该校共有名学生,则课外知识测试成绩能得优秀的同学大约有名
7.已知甲 乙 丙 丁 戊五位同学高一入学时年龄的平均数 中位数均为16,方差为0.8,则三年后,下列判断错误的是( )
A.这五位同学年龄的平均数变为19 B.这五位同学年龄的中位数变为19
C.这五位同学年龄的方差仍为0.8 D.这五位同学年龄的方差变为3.8
8.有13名同学参加百米竞赛,预赛成绩各不相同,要取前6名参加决赛,小明同学已经知道了自己的成绩,为了判断自己是否能进入决赛,他还需要知道13名同学成绩的( )
A.平均数 B.众数 C.中位数 D.方差
9.若样本数据,,…,的标准差为,则数据,,…,的标准差为( )
A. B. C. D.
10.某赛季甲乙两名篮球运动员在若干场比赛中的得分情况如下:
甲:21、22、23、25、28、29、30、30;
乙:14、16、23、26、28、30、33、38.
则下列描述合理的是( )
A.甲队员每场比赛得分的平均值大 B.乙队员每场比赛得分的平均值大
C.甲队员比赛成绩比较稳定 D.乙队员比赛成绩比较稳定
11.2020年宿州市某中学参加高中数学建模(应用)能力测试,高一年级有60人,高二年级有40人.高一的平均成绩为70分,高二的平均成绩为80分,则参加测试的100名学生的平均成绩为( )
A.72分 B.73分 C.74分 D.75分
12.已知甲 乙两组数据(已按从小到大的顺序排列):甲组:27,28,39,40,m,50;乙组:24,n,34,43,48,52.若这两组数据的30百分位数 80百分位数分别相等,则等于( )
A. B. C. D.
13.某学校组建了演讲,舞蹈 航模 合唱,机器人五个社团,全校名学生每人都参加且只参加其中一个社团,校团委从这名学生中随机选取部分学生进行调查,并将调查结果绘制了如下不完整的两个统计图:
则选取的学生中参加机器人社团的学生数为( )
A. B. C. D.
14.年月日,习近平总书记在学校考察调研时提出“文明其精神,野蛮其体魄”,“野蛮其体魄”就是强生健体,青少年的体质状况不仅关乎个人成长和家庭幸福,也关乎国家未来和民族希望,为落实《国家学生体质健康标准》达标测试工作,全面提升学生的体质健康水平,某校在高二年级随机抽取部分男生,测试立定跳远项目,依据测试数据绘制了如图所示的频率分布直方图.已知立定跳远以上成绩为及格,以上成绩为优秀,根据图中的样本数据估计该校高二年级男生立定跳远项目的及格率和优秀率分别是( )
A.72.5%,5% B.78.75%,10% C.72.5%,10% D.78.75%,5%
15.某中学举行了一次“环保知识竞赛”活动,为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本量为n)进行统计,按照,,,,的分组作出如图所示的频率分布直方图,但不慎丢失了部分数据.已知得分在的有8人,在的有2人,由此推测频率分布直方图中的( )
A.0.04 B.0.03 C.0.02 D.0.01
二、填空题
16.一个容量为100的样本,其数据的分组与各组的频数如下表:
组别 [0,10) [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]
频数 12 13 24 15 16 13 7
则样本数据落在[10,40)上的频率为________.
17.已知某样本数据分别为1,4,3,a,6,且样本均值,则样本方差_________.
18.已知一组数据,,3,5的中位数为7,平均数为8,则______.
三、解答题
19.某公司为了解用户对其产品的满意程度,采用分层抽样的方法从A,B两个地区共抽取了500名用户,请用户根据满意程度对该公司品评分,该公司将收集到的数据按照,,,分组,绘制成评分频率分布直方图如下:
已知A地区用户约为40000人,B地区用户约为10000人.
(1)求该公司采用分层抽样的方法从A,B两个地区分别抽取的用户人数;
(2)根据频率分布直分图,估计B地区所有用户中,对该产品评分不低于80分的用户的人数;
(3)根据频率分布直方图,估计A地区抽取的400名用户对该公司产品的评分的平均值为,B地区抽取的100名用户对该公司产品的评分的平均值为,以及A,B两个地区抽取的500名用户对该公司产品的评分的平均值为,试比较和的大小.(结论不要求证明)
20.鱼卷是泉州十大名小吃之一,不但本地人喜欢,而且深受外来游客的赞赏.小张从事鱼卷生产和批发多年,有着不少来自零售商和酒店的客户当地的习俗是农历正月不生产鱼卷,客户正月所需要的鱼卷都会在上一年农历十二月底进行一次性采购小张把去年年底采购鱼卷的数量x(单位:箱)在的客户称为“熟客”,并把他们去年采购的数量制成下表:
采购数x
客户数 10 10 5 20 5
(1)根据表中的数据作出频率分布直方图,并估计采购数在168箱以上(含168箱)的“熟客”人数;
(2)若去年年底“熟客”们采购的鱼卷数量占小张去年年底总的销售量的,估算小张去年年底总的销售量(同一组中的数据用该组区间的中点值为代表);
(3)由于鱼卷受到游客们的青睐,小张做了一份市场调查,决定今年年底是否在网上出售鱼卷,若不在网上出售鱼卷,则按去年的价格出售,每箱利润为20元,预计销售量与去年持平;若在网上出售鱼卷,则需把每箱售价下调2至5元,且每下调m元()销售量可增加1000m箱,求小张今年年底收入Y(单位:元)的最大值.
21.某校根据该校高一年级100名学生的英语成绩(不包括听力部分)得到如下频数分布表:
分组
频数 8 24 36 28 4
(1)根据频数分布表,作出这些数据的频率分布直方图,并求这100名学生英语成绩(不包括听力部分)的平均分(同一组中的数据用该组区间的中间值作代表);
(2)若这100名学生英语成绩的优秀率为,求英语成绩为优秀的分数线(保留整数位).
22.生产过程中,测得纤维产品的纤度(表示纤细的一种量),共有100个数据,将数据分组如下表:
分组 频数 频率
4
25
30
29
10
2
合计 100
(1)完成频率分布表,并画出频率分布直方图;
(2)估计纤度落在内的可能性及纤度小于的可能性各是多少?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
可不用动笔,直接得到答案,亦可采用特殊数据,特值法筛选答案.
【详解】
设9位评委评分按从小到大排列为.
则①原始中位数为,去掉最低分,最高分,后剩余,
中位数仍为,A正确.
②原始平均数,后来平均数
平均数受极端值影响较大,与不一定相同,B不正确
③
由②易知,C不正确.
④原极差,后来极差可能相等可能变小,D不正确.
本题旨在考查学生对中位数、平均数、方差、极差本质的理解.
2.A
平均数是次品数与相应的频率乘积之和.
【详解】
设数据xi出现的频率为pi(i=1,2,…,n),则x1,x2,…,xn的平均数为
x1p1+x2p2+…+xnpn=0×0.5+1×0.2+2×0.05+3×0.2+4×0.05=1.1.
故选:A
3.D
根据题意计算对应平均值、极差和方差,进行比较,逐一判断选项正误即可.
【详解】
选项A中,甲的平均分为,丙的平均分为,故甲的平均得分比丙的平均得分低,故错误;
选项B中,乙的得分极差为,丁的得分极差为,极差相等,故错误;
选项C中,不清楚两题的具体分值是否相同,所以不能通过平均分判断第4题相关知识一定比第2题相关知识掌握好,故错误;
选项D中,第3题得分的平均值为,
故方差为,
第5题得分的平均分为,
故方差为,
故第3题得分的方差比第5题得分的方差小.故正确.
故选:D.
4.D
由频率分布直方图易得四位同学的中位数,可比较出大小,再分别计算出平均数进行比较,可得选项.
【详解】
甲 乙 丙三位同学的成绩中位数都是80,丁的成绩中位数大于80;
甲的平均成绩为,
乙的平均成绩为,
丙的平均成绩为,
丁的平均成绩为
故选:D.
5.A
首先设出新农村建设前的经济收入为M,根据题意,得到新农村建设后的经济收入为2M,之后从图中各项收入所占的比例,得到其对应的收入是多少,从而可以比较其大小,并且得到其相应的关系,从而得出正确的选项.
【详解】
设新农村建设前的收入为M,而新农村建设后的收入为2M,
则新农村建设前种植收入为0.6M,而新农村建设后的种植收入为0.74M,所以种植收入增加了,所以A项不正确;
新农村建设前其他收入我0.04M,新农村建设后其他收入为0.1M,故增加了一倍以上,所以B项正确;
新农村建设前,养殖收入为0.3M,新农村建设后为0.6M,所以增加了一倍,所以C项正确;
新农村建设后,养殖收入与第三产业收入的综合占经济收入的,所以超过了经济收入的一半,所以D正确;
故选A.
点睛:该题考查的是有关新农村建设前后的经济收入的构成比例的饼形图,要会从图中读出相应的信息即可得结果.
6.C
由百分比图知,成绩为100分、80分、60分、40分的百分比分别为,结合各项的描述即可判断其正误.
【详解】
由图知,及格率为,故A错误.
该测试满分同学的百分比为,即有名,B错误.
由图知,中位数为分,平均数为分,故C正确.
由题意,名学生成绩能得优秀的同学有,故D错误.
故选:C
7.D
利用平均数、中位数、方差的定义直接求解.
【详解】
甲、乙、丙、丁、戊五位同学高一入学时年龄的平均数、中位数均为16,方差位0.8,
三年后,
这五位同学年龄的平均数变为16+3=19,故A正确;
这五位同学年龄的中位数变为16+3=19,故B正确;
这五位同学的方差不变,仍为0.8,故C正确,D错误.
故选:D.
8.C
成绩由小到大排列,能否进入决赛就看小明成绩排名是否在第7以前即可得解.
【详解】
把13名同学成绩按由大到小排列,取成绩靠前的6个成绩进入决赛,即最中间一个数之前的6个成绩进入决赛,
13个成绩按由大到小排列时,最中间一个数即是中位数.
故选:C
9.B
首先设原数据的平均数为,则新数据的平均数为,然后结合原数据的方差,利用方差的公式计算得出新数据的方差,再求出标准差即可.
【详解】
设原数据的平均数为,则新数据的平均数为,
则原数据的方差为,
则新数据的方差为:
.
故数据,,…,的标准差为:8.
故选:B.
10.C
计算均值,再根据数据的集中度判断.
【详解】
甲的均值为,
乙的均值为,
两者均值相同,甲的方差为
乙的方差为
,
甲的方差小于乙的方差,甲稳定.
故选:C.
11.C
根据平均值的计算公式,由题中条件直接计算,即可得出结果.
【详解】
由题意可得,参加测试的100名学生的平均成绩为.
故选:C.
12.A
根据百分位数的定义并结合已知条件求出的值,由此可得的值.
【详解】
因为×6=1.8,×6=4.8,所以30百分位数为第二个数,即n=28,80百分位数为第五个数即m=48,所以==.
故选:A
13.B
根据演讲的人数,求得本次调查的人数为人,进而求得机器人所占的比例,即可求解.
【详解】
由题意,本次调查的人数为人,
其中合唱比赛所占的比例为,
所以机器人所占的比例为,
所以选取的学生中参加机器人社团的学生数为人.
故选:B.
14.B
计算以上的矩形的面积之和,可得出该校高二年级男生立定跳远项目的及格率,计算以上的矩形的面积之和,可得出该校高二年级男生立定跳远项目的优秀率.
【详解】
由题意可知,该校高二年级男生立定跳远项目的及格率为,
该校高二年级男生立定跳远项目的优秀率为.
故选:B.
15.B
根据频率分布直方图,先求得抽取学生的人数.
【详解】
得分在的有8人, 得分在的频率为
所以抽取中的人数为人
在的有2人,所以在的频率为,所以
∴由频率分布直方图各小矩形面积和为1,得.
解得.
故选:B.
本题考查了频率分布直方图的意义,补全频率分布直方图,属于基础题.
16.0.52
根据图表,样本数据落在[10,40)上的频数为13+24+15=52,根据频率公式即可得解.
【详解】
样本数据落在[10,40)上的频数为13+24+15=52.
则样本数据落在[10,40)上的频率为=0.52.
故答案为:0.52
17.##
先求得的值,然后求得样本方差.
【详解】
依题意,
所以.
故答案为:
18.135
先由平均数为8,求出,然后分和讨论,当时,不妨设,再分,和三种情况讨论即可
【详解】
因为一组数据,,3,5的平均数为8,
所以,解得,
若,则,此时四个数为,显然中位数不是7,
不妨设,若,则,此时4个数排列为,中位数为4,不合题意,
若时,则,此时4个数排列为,显然中位数不是7,
若,则4个数排列为,则中位数为,解得,则,
所以,
故答案为:135
19.(1)地区抽取400户,地区抽取100户;(2)10;(3)当时,,时,,时,.
(1)根据分层抽样,样本比等于总体比求得抽取的用户人数;
(2)由频率分布图得出频率后可得所求人数;
(3)根据均值的定义求出,作差比较.
【详解】
(1)设A,B两个地区抽取的用户人数分别为,则,所以,;
(2)由频率分布图知,B地区所有用户中,对该产品评分不低于80分的用户频率为,人数;
(3)由题意,
,
所以当时,,时,,时,.
20.(1)见解析 17人(2)12000箱 (3)最大值为256000元.
(1)根据统计表作出频率分布直方图,再根据直方图即可求出,
(2)根据统计表和直方图即可求出,
(3)没有在网上出售鱼卷,则今年的年底小张的收入为(元,若网上出售鱼卷,则今年的年底的销售量为,即可求出的最大值,比较即可
【详解】
解: (1)作出频率分布直方图,如图
根据上图,可知采购量在168箱以上(含168箱)的“熟客”人数为
(2)去年年底“熟客”所采购的鱼卷总数大约为
(箱)
小张去年年底总的销售量为(箱)
(3)若不在网上出售鱼卷,则今年年底小张的收入为(元);
若在网上出售鱼卷,则今年年底的销售量为箱,每箱的利润为,
则今年年底小张的收入为
,
当时, 取得最大值256000
∵,
∴小张今年年底收入的最大值为256000元.
本题考查了频率分布直方图的计算问题,属于基础题.
21.(1)频率分布直方图答案见解析,平均分;(2)分数线为99.
(1)作出频率分布直方图,结合频率分布直方图的性质能求出平均分.(2)由题可知,,的频率为0.04,,的频率为0.28,由此能求出英语成绩为优秀的分数线.
【详解】
解:(1)频率分布直方图如下:
平均分.
(2)由题可知,的频率为0.04,
的频率为0.28,
因为这100名学生英语成绩的优秀率为,所以成绩优秀的分数线在之间,
设优秀成绩的分数线为x,则有.1
解得.
故英语成绩为优秀的分数线为99.
22.(1)答案见解析;(2),.
(1)根据题意,由频率与频数的关系,计算可得各组的频率,进而可以做出频率分布表,结合分布表,进而可以做出频率分步直方图;
(2)由频率分布表可得纤度落在中的可能性,并可计算纤度小于的可能性.
【详解】
频率分布表如下:
分组 频数 频率
4
25
30
29
10
合计
频率分布直方图如图所示.
(2)利用样本估计总体,则纤度落在的可能性即为纤度落在的频率,即为.
纤度小于的可能性即为纤度小于的频率,即为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
