华师大版八下数学 18.1.2平行四边形对角线的性质 教案
文档属性
| 名称 | 华师大版八下数学 18.1.2平行四边形对角线的性质 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 69.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 00:00:00 | ||
图片预览

文档简介
18.1.2 平行四边形对角线的性质
知识技能目标
1.理解和掌握发现平行四边形的对角线互相平分的特征;
2.了解两平行线之间距离的概念;
3.会利用平行四边形的特征进行相关的计算和说理.
过程性目标
1.通过实践操作,感受两平行线之间距离处处相等;
2.体会两平行线之间的距离、点到直线之间距离、点与点之间距离的相互联系与转化.
教学重点:平行四边形对角线互相平分的性质以及性质的应用。
教学难点:综合运用平行四边形的性质进行有关的论证和计算。
课前准备
准备一些方格纸.
教学过程
一、创设情境
师 请同学们画一个ABCD,对角线AC和BD相交于O,用刻度尺测量OA,OB,OC,OD的大小关系.再画一个试一试.
生 OA = OC, OB = OD.
二、探究归纳
师 很好!说明平行四边形的对角线互相平分.
在上节课平行四边形的旋转过程中,我们也观察到
了OA与OB,OC与OD能够互相重合,请同学们用
学过的知识来说明这一现象
生 ABCD是一个中心对称图形,O是它的对称中心,
OA = OC, OB = OD.
师 回答得非常正确,由此我们得出了平行四边形的又一个重要特征:
师生 平行四边形的对角线互相平分
四边形ABCD是平行四边形,
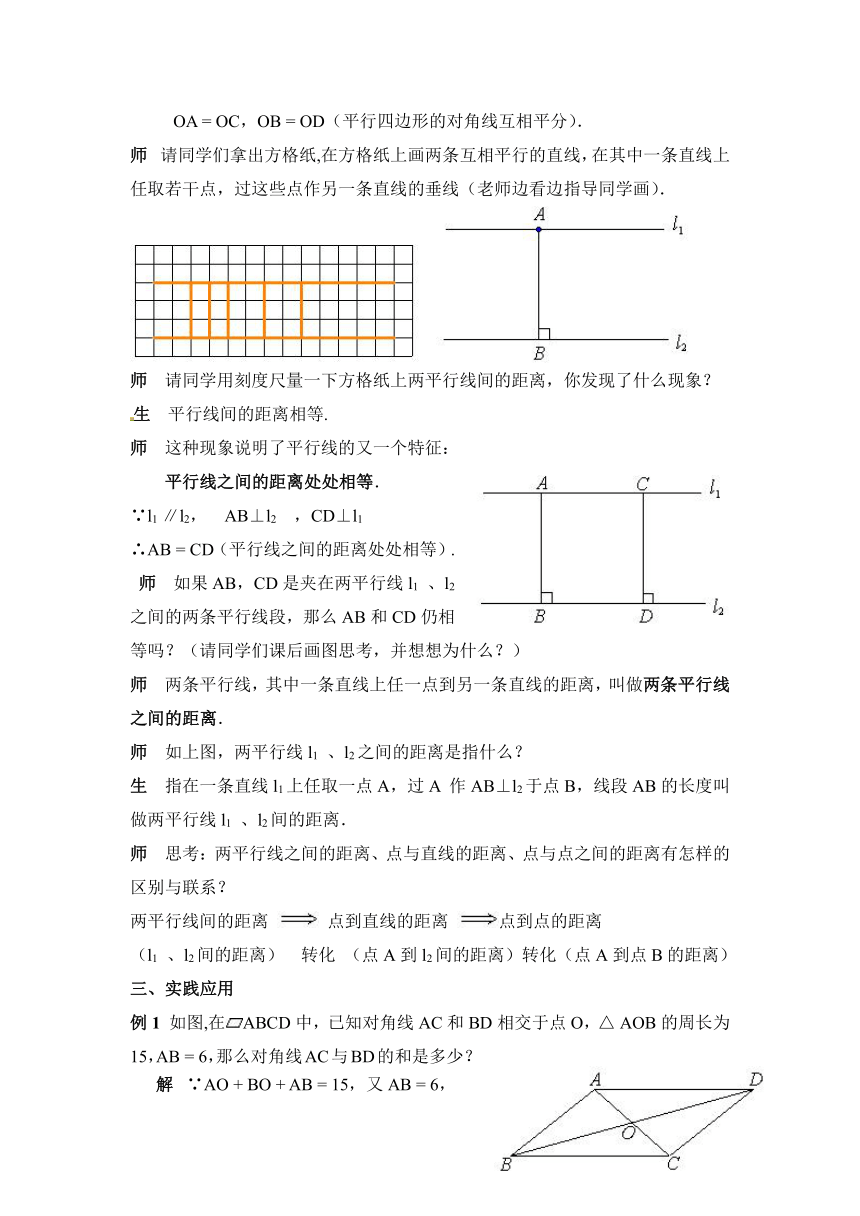
OA = OC,OB = OD(平行四边形的对角线互相平分).
师 请同学们拿出方格纸,在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线(老师边看边指导同学画).
师 请同学用刻度尺量一下方格纸上两平行线间的距离,你发现了什么现象?
生 平行线间的距离相等.
师 这种现象说明了平行线的又一个特征:
平行线之间的距离处处相等.
∵l1 ∥l2, AB⊥l2 ,CD⊥l1
∴AB = CD(平行线之间的距离处处相等).
师 如果AB,CD是夹在两平行线l1 、l2之间的两条平行线段,那么AB和CD仍相等吗?(请同学们课后画图思考,并想想为什么?)
师 两条平行线,其中一条直线上任一点到另一条直线的距离,叫做两条平行线之间的距离.
师 如上图,两平行线l1 、l2之间的距离是指什么?
生 指在一条直线l1上任取一点A,过A 作AB⊥l2于点B,线段AB的长度叫做两平行线l1 、l2间的距离.
师 思考:两平行线之间的距离、点与直线的距离、点与点之间的距离有怎样的区别与联系?
两平行线间的距离 点到直线的距离 点到点的距离
(l1 、l2间的距离) 转化 (点A到l2间的距离)转化(点A到点B的距离)
三、实践应用
例1 如图,在ABCD中,已知对角线AC和BD相交于点O,△ AOB的周长为15,AB = 6,那么对角线AC与BD的和是多少?
解 ∵AO + BO + AB = 15,又AB = 6,
∴AO + BO = 15-6 = 9.
又∵四边形ABCD是平行四边形,
∴AO = CO,BO = DO(平行四边形的对角线互相平分).
即AC + BD = 2AO + 2 BO = 2(AO + BO)
=2×9 = 18.
例2 如上图, ABCD的周长为60cm,对角线AC,BD相交于点O,△ AOB的周长比△BOC的周长少8cm,求AB,BC的长.
解 ∵AB + BC + CD + DA = 60,
(BC + BO + CO)-(AB + AO + BO)= 8,
又四边形ABCD是平行四边形,
∴AB = CD,AD = BC(平行四边形的对边平行).
AO = CO,BO = DO(平行四边形的对角线互相平分).
从而AB + BC =30,BC-AB = 8,
得BC =19,AB =11.
例3已知ABCD中,对角线AC,BD相交于点O,说明S△ABC= S△DBC.
解 过点A作AE⊥BC于点E、过点D作DF⊥BC交BC的延长线于点F.
∵AD∥BC, AE⊥BC,DF⊥BC,
∴AE = DF(平行线之间的距离处处相等),
∴,
即S△ABC= S△DBC.
四、交流反思
师 通过两节课的讨论与学习,我们的收获真不小,已掌握了平行四边形的哪些特征,你能回想出来吗?
1.平行四边形的对边平行且相等;
2.平行四边形的对角相等;
3.平行四边形的对角线互相平分;
4.平行线之间的距离处处相等.
五、检测反馈
1.已知在ABCD中,两条对角线AC,BD相交于点O,指出图形中相等的线段.
2.如图,如果直线 l1 ∥l2,那么△ABC的面积和△DBC的面积是相等的,你能说出理由吗?你还能在这两条平行线l1 、l2之间画出其他与△ABC面积相等的三角形吗?
3.ABCD中, 对角线AC,BD相交于点O,已知AO比AB短2cm,BO比AB长2cm,BO是AO的2倍,求AC,BD的长.
4.如图,ABCD中,AE、CF分别平分∠BAD和∠BCD,试说明AC、EF互相平分.
( http: / / zhdduya100. / ) ( http: / / zhdduya100. / )
知识技能目标
1.理解和掌握发现平行四边形的对角线互相平分的特征;
2.了解两平行线之间距离的概念;
3.会利用平行四边形的特征进行相关的计算和说理.
过程性目标
1.通过实践操作,感受两平行线之间距离处处相等;
2.体会两平行线之间的距离、点到直线之间距离、点与点之间距离的相互联系与转化.
教学重点:平行四边形对角线互相平分的性质以及性质的应用。
教学难点:综合运用平行四边形的性质进行有关的论证和计算。
课前准备
准备一些方格纸.
教学过程
一、创设情境
师 请同学们画一个ABCD,对角线AC和BD相交于O,用刻度尺测量OA,OB,OC,OD的大小关系.再画一个试一试.
生 OA = OC, OB = OD.
二、探究归纳
师 很好!说明平行四边形的对角线互相平分.
在上节课平行四边形的旋转过程中,我们也观察到
了OA与OB,OC与OD能够互相重合,请同学们用
学过的知识来说明这一现象
生 ABCD是一个中心对称图形,O是它的对称中心,
OA = OC, OB = OD.
师 回答得非常正确,由此我们得出了平行四边形的又一个重要特征:
师生 平行四边形的对角线互相平分
四边形ABCD是平行四边形,
OA = OC,OB = OD(平行四边形的对角线互相平分).
师 请同学们拿出方格纸,在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线(老师边看边指导同学画).
师 请同学用刻度尺量一下方格纸上两平行线间的距离,你发现了什么现象?
生 平行线间的距离相等.
师 这种现象说明了平行线的又一个特征:
平行线之间的距离处处相等.
∵l1 ∥l2, AB⊥l2 ,CD⊥l1
∴AB = CD(平行线之间的距离处处相等).
师 如果AB,CD是夹在两平行线l1 、l2之间的两条平行线段,那么AB和CD仍相等吗?(请同学们课后画图思考,并想想为什么?)
师 两条平行线,其中一条直线上任一点到另一条直线的距离,叫做两条平行线之间的距离.
师 如上图,两平行线l1 、l2之间的距离是指什么?
生 指在一条直线l1上任取一点A,过A 作AB⊥l2于点B,线段AB的长度叫做两平行线l1 、l2间的距离.
师 思考:两平行线之间的距离、点与直线的距离、点与点之间的距离有怎样的区别与联系?
两平行线间的距离 点到直线的距离 点到点的距离
(l1 、l2间的距离) 转化 (点A到l2间的距离)转化(点A到点B的距离)
三、实践应用
例1 如图,在ABCD中,已知对角线AC和BD相交于点O,△ AOB的周长为15,AB = 6,那么对角线AC与BD的和是多少?
解 ∵AO + BO + AB = 15,又AB = 6,
∴AO + BO = 15-6 = 9.
又∵四边形ABCD是平行四边形,
∴AO = CO,BO = DO(平行四边形的对角线互相平分).
即AC + BD = 2AO + 2 BO = 2(AO + BO)
=2×9 = 18.
例2 如上图, ABCD的周长为60cm,对角线AC,BD相交于点O,△ AOB的周长比△BOC的周长少8cm,求AB,BC的长.
解 ∵AB + BC + CD + DA = 60,
(BC + BO + CO)-(AB + AO + BO)= 8,
又四边形ABCD是平行四边形,
∴AB = CD,AD = BC(平行四边形的对边平行).
AO = CO,BO = DO(平行四边形的对角线互相平分).
从而AB + BC =30,BC-AB = 8,
得BC =19,AB =11.
例3已知ABCD中,对角线AC,BD相交于点O,说明S△ABC= S△DBC.
解 过点A作AE⊥BC于点E、过点D作DF⊥BC交BC的延长线于点F.
∵AD∥BC, AE⊥BC,DF⊥BC,
∴AE = DF(平行线之间的距离处处相等),
∴,
即S△ABC= S△DBC.
四、交流反思
师 通过两节课的讨论与学习,我们的收获真不小,已掌握了平行四边形的哪些特征,你能回想出来吗?
1.平行四边形的对边平行且相等;
2.平行四边形的对角相等;
3.平行四边形的对角线互相平分;
4.平行线之间的距离处处相等.
五、检测反馈
1.已知在ABCD中,两条对角线AC,BD相交于点O,指出图形中相等的线段.
2.如图,如果直线 l1 ∥l2,那么△ABC的面积和△DBC的面积是相等的,你能说出理由吗?你还能在这两条平行线l1 、l2之间画出其他与△ABC面积相等的三角形吗?
3.ABCD中, 对角线AC,BD相交于点O,已知AO比AB短2cm,BO比AB长2cm,BO是AO的2倍,求AC,BD的长.
4.如图,ABCD中,AE、CF分别平分∠BAD和∠BCD,试说明AC、EF互相平分.
( http: / / zhdduya100. / ) ( http: / / zhdduya100. / )
