华师大版八下数学 19.2.1菱形的性质 教案
文档属性
| 名称 | 华师大版八下数学 19.2.1菱形的性质 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 499.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 00:00:00 | ||
图片预览

文档简介
菱形的性质
教学目标:
1、让学生动手探索菱形的定义,以及和平行四边形的联系与区别
2、掌握菱形的性质并会用它进行有关的论证和计算
教学重点:
掌握并应用菱形的性质
教学难点
在实际问题中对菱形性质的运用
1、设疑自探
对称性
边
角
对角线
1、复习引入
平行四边形 的性质
2、感受生活
下面我们一起来观察生活中的一些图案,图案中是否有我们学过的平行四边形?
再仔细观察它和我们已经学过的平行四边形又有怎样的不同?
展示平行四边形,它的一边平行移动,直到有两邻边相等,这样特殊的平行四边就是我们今天要研究的图形,菱形
菱形是有一组邻边相等的平行四边形
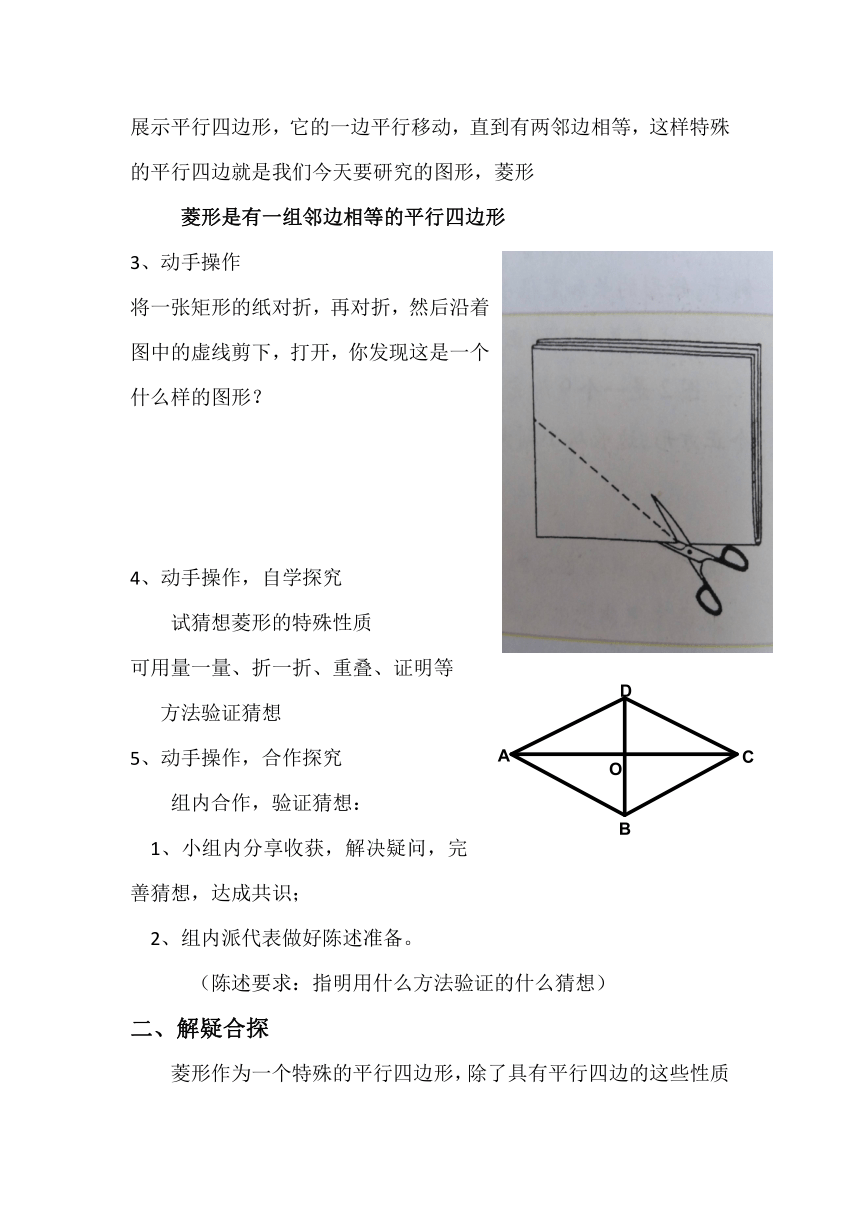
3、动手操作
将一张矩形的纸对折,再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形?
4、动手操作,自学探究
试猜想菱形的特殊性质
可用量一量、折一折、重叠、证明等
方法验证猜想
5、动手操作,合作探究
组内合作,验证猜想:
1、小组内分享收获,解决疑问,完善猜想,达成共识;
2、组内派代表做好陈述准备。
(陈述要求:指明用什么方法验证的什么猜想)
二、解疑合探
菱形作为一个特殊的平行四边形,除了具有平行四边的这些性质外,还具有怎样的特殊性质,看看你刚才剪下的菱形,猜想它具有哪些特殊性质?(提问)利用手中的菱形,完成自学探究,小组内合作探究,结果展示
1、性质
平行四边形的性质 菱形的特殊性质
对称性:中心对称 轴对称
边: 对边平行且相等 四条边相等
角: 对角相等
对角线: 对角线互相平分 对角线互相垂直
2、证明:菱形的对角线互相垂直
已知:如图,菱形ABCD
求证:AC⊥BD
证明:∵菱形ABCD
∴AD = CD,AB = BC,AO=OC
∴OD⊥AC,
即:AC⊥BD
3、质疑再探
通过前面的探究学习,你还有哪些疑问或看法?
两条对角线分出四个怎样的三角形?
对角线平分了一组对角
四、自主学习,巩固新知
如图,四边形ABCD是菱形,对角线AC、BD相交于点O,且 AB = 5,AO = 4,
则(1)菱形的周长为 _____ ;
(2)BO = ______ , AC =______,
BD =______;
(3) = _______;
(4) = ______ ×=______× =_______
五、合作学习,探索新知
通过“牛刀小试”的计算,你能发现菱形对角线的长与面积有什么关系吗?这个结论对所有菱形都成立吗?请简单说明理由。
先独立思考,再组内交流合作
菱形的面积公式
六、学以致用
若视频中的跳伞队员们组成了如图所示的菱形ABCD ,其边长为60m, ∠BAD=60°,请你求出两条对角线的长和菱形的面积(结果保留根号)。
七、课堂总结
1.这节课我的收获是··· ···
2.我的困惑是··· ···
八、分级达标,检验新知
1、下列性质中,菱形具有但平行四边形不一定具有的是( )
A、对边相等 B、对角相等
C、对角线互相垂直 D、对边平行
2、已知菱形ABCD中, 若∠ABC = 100°,则∠ABD = ____________ ;
3、如图,这是工人制作的一种铁艺菱形图案,其中AC=6cm,BD比AC长2cm。请你帮他算一下,(1)该图案的面积。(2)至少要多长铁丝才能制作出该图案?
D
C
C
D
A
B
A
B
C
D
O
A
B
C
D
E
A
D
C
B
O
教学目标:
1、让学生动手探索菱形的定义,以及和平行四边形的联系与区别
2、掌握菱形的性质并会用它进行有关的论证和计算
教学重点:
掌握并应用菱形的性质
教学难点
在实际问题中对菱形性质的运用
1、设疑自探
对称性
边
角
对角线
1、复习引入
平行四边形 的性质
2、感受生活
下面我们一起来观察生活中的一些图案,图案中是否有我们学过的平行四边形?
再仔细观察它和我们已经学过的平行四边形又有怎样的不同?
展示平行四边形,它的一边平行移动,直到有两邻边相等,这样特殊的平行四边就是我们今天要研究的图形,菱形
菱形是有一组邻边相等的平行四边形
3、动手操作
将一张矩形的纸对折,再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形?
4、动手操作,自学探究
试猜想菱形的特殊性质
可用量一量、折一折、重叠、证明等
方法验证猜想
5、动手操作,合作探究
组内合作,验证猜想:
1、小组内分享收获,解决疑问,完善猜想,达成共识;
2、组内派代表做好陈述准备。
(陈述要求:指明用什么方法验证的什么猜想)
二、解疑合探
菱形作为一个特殊的平行四边形,除了具有平行四边的这些性质外,还具有怎样的特殊性质,看看你刚才剪下的菱形,猜想它具有哪些特殊性质?(提问)利用手中的菱形,完成自学探究,小组内合作探究,结果展示
1、性质
平行四边形的性质 菱形的特殊性质
对称性:中心对称 轴对称
边: 对边平行且相等 四条边相等
角: 对角相等
对角线: 对角线互相平分 对角线互相垂直
2、证明:菱形的对角线互相垂直
已知:如图,菱形ABCD
求证:AC⊥BD
证明:∵菱形ABCD
∴AD = CD,AB = BC,AO=OC
∴OD⊥AC,
即:AC⊥BD
3、质疑再探
通过前面的探究学习,你还有哪些疑问或看法?
两条对角线分出四个怎样的三角形?
对角线平分了一组对角
四、自主学习,巩固新知
如图,四边形ABCD是菱形,对角线AC、BD相交于点O,且 AB = 5,AO = 4,
则(1)菱形的周长为 _____ ;
(2)BO = ______ , AC =______,
BD =______;
(3) = _______;
(4) = ______ ×=______× =_______
五、合作学习,探索新知
通过“牛刀小试”的计算,你能发现菱形对角线的长与面积有什么关系吗?这个结论对所有菱形都成立吗?请简单说明理由。
先独立思考,再组内交流合作
菱形的面积公式
六、学以致用
若视频中的跳伞队员们组成了如图所示的菱形ABCD ,其边长为60m, ∠BAD=60°,请你求出两条对角线的长和菱形的面积(结果保留根号)。
七、课堂总结
1.这节课我的收获是··· ···
2.我的困惑是··· ···
八、分级达标,检验新知
1、下列性质中,菱形具有但平行四边形不一定具有的是( )
A、对边相等 B、对角相等
C、对角线互相垂直 D、对边平行
2、已知菱形ABCD中, 若∠ABC = 100°,则∠ABD = ____________ ;
3、如图,这是工人制作的一种铁艺菱形图案,其中AC=6cm,BD比AC长2cm。请你帮他算一下,(1)该图案的面积。(2)至少要多长铁丝才能制作出该图案?
D
C
C
D
A
B
A
B
C
D
O
A
B
C
D
E
A
D
C
B
O
