华师大版八下数学 19.2.2菱形的判定 教案
文档属性
| 名称 | 华师大版八下数学 19.2.2菱形的判定 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 91.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 19:48:50 | ||
图片预览

文档简介
菱形的判定
教学目标:
一、知识与技能
能说出菱形的两个判定定理,并会用它进行相关的论证和计算.
二、过程与方法
1.经历探究菱形判定条件的过程,通过操作、观察、猜想、证明的过程,培养学生的科学探索精神.
2.探索并掌握菱形的判定方法.
3.利用菱形的判定方法进行合理的论证和计算.
三、情感态度与价值观
1.让学生在探究过程中加深对菱形的理解,养成主动探索的学习习惯.
2.通过菱形与矩形判定方法的类比,进一步体会类比的思想方法的作用.
教学重点: 菱形的判定方法.
教学难点: 探究菱形的判定条件并合理利用它进行论证和计算.
教具准备: 多媒体课件
教学过程
一、创设问题情境,引入新课
想一想:菱形和矩形分别比平行四边形多了哪些性质?怎样判定一个四边形是矩形?
(让学生回忆并说出菱形和矩形各自的性质,教师用对比的形式播放课件)
矩 形 菱 形
性质 1.四个角都是直角 1.四条边都相等
2.对角线相等 2.对角线互相垂直且平分一组对角
判定 有一个角是直角的平行四边形
2.三个角是直角的四边形
角线相等的平行四边形
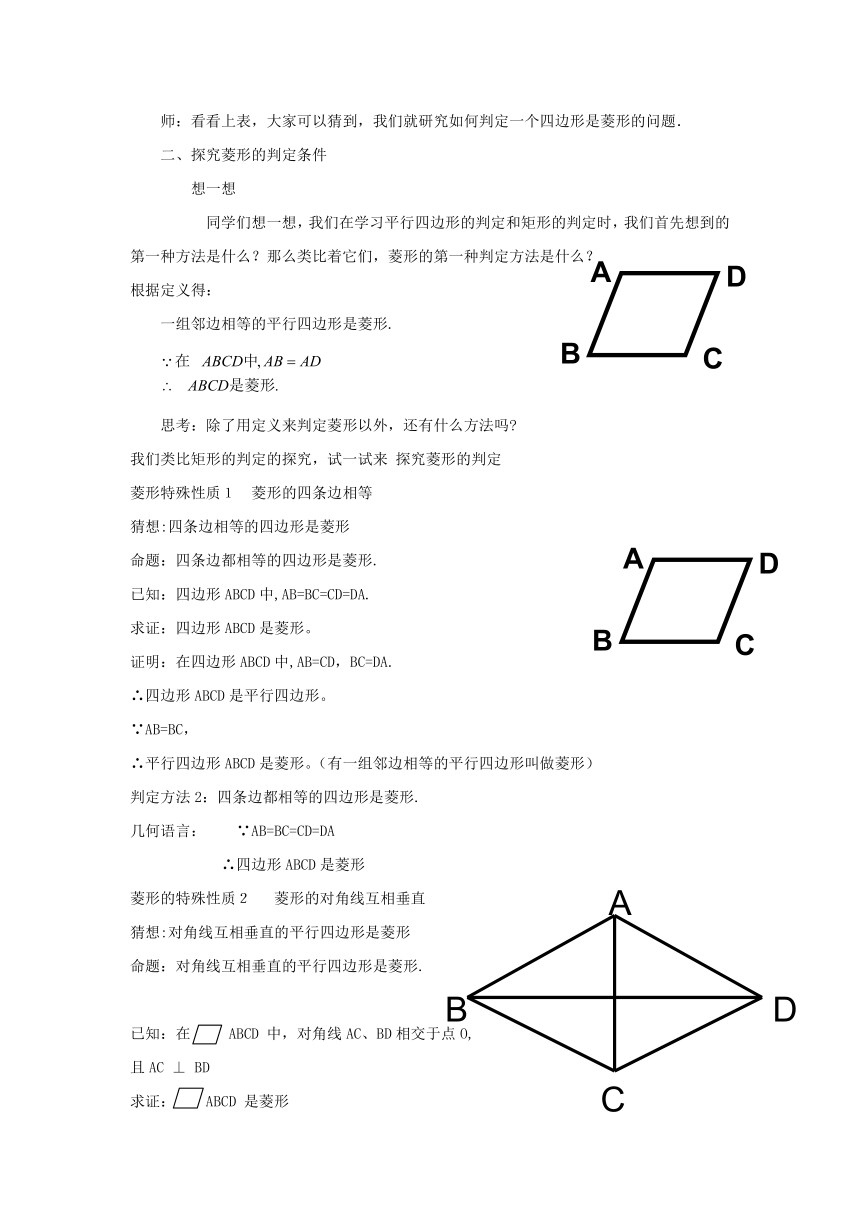
师:看看上表,大家可以猜到,我们就研究如何判定一个四边形是菱形的问题.
2、探究菱形的判定条件
想一想
同学们想一想,我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么?那么类比着它们,菱形的第一种判定方法是什么?
根据定义得:
一组邻边相等的平行四边形是菱形.
思考:除了用定义来判定菱形以外,还有什么方法吗
我们类比矩形的判定的探究,试一试来 探究菱形的判定
菱形特殊性质1 菱形的四条边相等
猜想:四条边相等的四边形是菱形
命题:四条边都相等的四边形是菱形.
已知:四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形。
证明:在四边形ABCD中,AB=CD,BC=DA.
∴四边形ABCD是平行四边形。
∵AB=BC,
∴平行四边形ABCD是菱形。(有一组邻边相等的平行四边形叫做菱形)
判定方法2:四条边都相等的四边形是菱形.
几何语言: ∵AB=BC=CD=DA
∴四边形ABCD是菱形
菱形的特殊性质2 菱形的对角线互相垂直
猜想:对角线互相垂直的平行四边形是菱形
命题:对角线互相垂直的平行四边形是菱形.
已知:在 ABCD 中,对角线AC、BD相交于点O,
且AC ⊥ BD
求证: ABCD 是菱形
证明:∵四边形ABCD是平行四边形
∴OA=OC
又∵ AC ⊥ BD;
∴BA=BC(线段垂直平分线上的点到线段两个端点的距离相等)
∴ ABCD是菱形(有一组邻边相等的平行四边形叫做菱形).
判定方法3:对角线互相垂直的平行四边形是菱形
几何语言:∵四边形ABCD是平行四边形且AC⊥BD
∴ □ABCD是菱形
归纳:请同学们总结今天学习了几种菱形的判定方法
三、例题讲解:
例1、如图,在矩形ABCD中,点E、F、G、H分别是四条边的中点,试问四边形EFGH是什么图形?并说明理由。
解:在矩形ABCD中,
∠A= ∠B,AD=BC;
∵E、F、G、H是四条边的中点,
∴AE=EB,AH=BF,
∴ △AEH≌ △BEF(SAS)
∴EH=EF;
同理可得:EF=FG,FG=HG,
∴EH=EF=FG=GH,
∴四边形ABCD是菱形。(有四条边相等的四边形是菱形。)
例2、如图,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F。
求证:四边形AECF的菱形。
证明:在矩形ABCD中,
∵AD∥BC,
∴ ∠DAC= ∠BCA, ∠AEF= ∠CFE
又∵EF平分AC,
∴OA=OC,
△AOE≌ △COF(AAS)
∴OE=OF。
∵OA=OC,OE=OF,
∴四边形ABCD是平行四边形。
∵平行四边形ABCD中,AC⊥EF,
∴四边形ABCD是菱形。(对角线互相垂直的平行四边形是菱形)
A
B
C
D
A
B
C
D
A
B
C
D
教学目标:
一、知识与技能
能说出菱形的两个判定定理,并会用它进行相关的论证和计算.
二、过程与方法
1.经历探究菱形判定条件的过程,通过操作、观察、猜想、证明的过程,培养学生的科学探索精神.
2.探索并掌握菱形的判定方法.
3.利用菱形的判定方法进行合理的论证和计算.
三、情感态度与价值观
1.让学生在探究过程中加深对菱形的理解,养成主动探索的学习习惯.
2.通过菱形与矩形判定方法的类比,进一步体会类比的思想方法的作用.
教学重点: 菱形的判定方法.
教学难点: 探究菱形的判定条件并合理利用它进行论证和计算.
教具准备: 多媒体课件
教学过程
一、创设问题情境,引入新课
想一想:菱形和矩形分别比平行四边形多了哪些性质?怎样判定一个四边形是矩形?
(让学生回忆并说出菱形和矩形各自的性质,教师用对比的形式播放课件)
矩 形 菱 形
性质 1.四个角都是直角 1.四条边都相等
2.对角线相等 2.对角线互相垂直且平分一组对角
判定 有一个角是直角的平行四边形
2.三个角是直角的四边形
角线相等的平行四边形
师:看看上表,大家可以猜到,我们就研究如何判定一个四边形是菱形的问题.
2、探究菱形的判定条件
想一想
同学们想一想,我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么?那么类比着它们,菱形的第一种判定方法是什么?
根据定义得:
一组邻边相等的平行四边形是菱形.
思考:除了用定义来判定菱形以外,还有什么方法吗
我们类比矩形的判定的探究,试一试来 探究菱形的判定
菱形特殊性质1 菱形的四条边相等
猜想:四条边相等的四边形是菱形
命题:四条边都相等的四边形是菱形.
已知:四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形。
证明:在四边形ABCD中,AB=CD,BC=DA.
∴四边形ABCD是平行四边形。
∵AB=BC,
∴平行四边形ABCD是菱形。(有一组邻边相等的平行四边形叫做菱形)
判定方法2:四条边都相等的四边形是菱形.
几何语言: ∵AB=BC=CD=DA
∴四边形ABCD是菱形
菱形的特殊性质2 菱形的对角线互相垂直
猜想:对角线互相垂直的平行四边形是菱形
命题:对角线互相垂直的平行四边形是菱形.
已知:在 ABCD 中,对角线AC、BD相交于点O,
且AC ⊥ BD
求证: ABCD 是菱形
证明:∵四边形ABCD是平行四边形
∴OA=OC
又∵ AC ⊥ BD;
∴BA=BC(线段垂直平分线上的点到线段两个端点的距离相等)
∴ ABCD是菱形(有一组邻边相等的平行四边形叫做菱形).
判定方法3:对角线互相垂直的平行四边形是菱形
几何语言:∵四边形ABCD是平行四边形且AC⊥BD
∴ □ABCD是菱形
归纳:请同学们总结今天学习了几种菱形的判定方法
三、例题讲解:
例1、如图,在矩形ABCD中,点E、F、G、H分别是四条边的中点,试问四边形EFGH是什么图形?并说明理由。
解:在矩形ABCD中,
∠A= ∠B,AD=BC;
∵E、F、G、H是四条边的中点,
∴AE=EB,AH=BF,
∴ △AEH≌ △BEF(SAS)
∴EH=EF;
同理可得:EF=FG,FG=HG,
∴EH=EF=FG=GH,
∴四边形ABCD是菱形。(有四条边相等的四边形是菱形。)
例2、如图,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F。
求证:四边形AECF的菱形。
证明:在矩形ABCD中,
∵AD∥BC,
∴ ∠DAC= ∠BCA, ∠AEF= ∠CFE
又∵EF平分AC,
∴OA=OC,
△AOE≌ △COF(AAS)
∴OE=OF。
∵OA=OC,OE=OF,
∴四边形ABCD是平行四边形。
∵平行四边形ABCD中,AC⊥EF,
∴四边形ABCD是菱形。(对角线互相垂直的平行四边形是菱形)
A
B
C
D
A
B
C
D
A
B
C
D
