沪科版数学八年级下册 19.2平行四边形-课件(共16张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 19.2平行四边形-课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1002.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 09:40:18 | ||
图片预览




文档简介
(共16张PPT)
世界七大数学难题
NP完全问题
霍奇猜想
庞加莱猜想
黎曼假设
杨-米尔斯存在性和质量缺口
纳卫尔-斯托可方程
BSD猜想
悬赏100万美金
在数学课上,老师提出了这样一个问题,用20米的绳子围成平行四边形,且边长是正整数,有多少种围法?小明是个聪明的孩子,很快得出了答案,你知道答案了吗?这时候老师接着提问,如果长边比短边长2米,那将怎样呢
创设情境 1分钟挑战
导入新课
19.2.1 平行四边形
生活中,平行四边形无处不在,那么它有哪些性质呢?今天我们就一起来探讨一下吧!
讲授新课
平行四边形边的相关概念
一
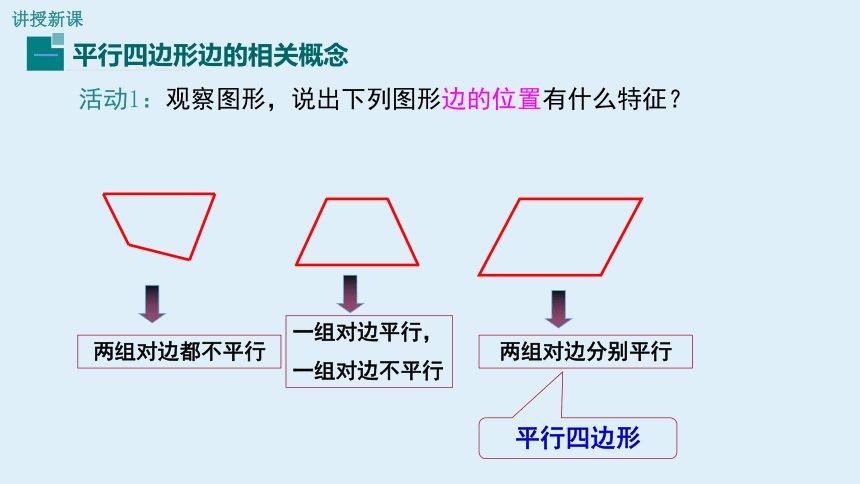
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
平行四边形
活动1:观察图形,说出下列图形边的位置有什么特征?
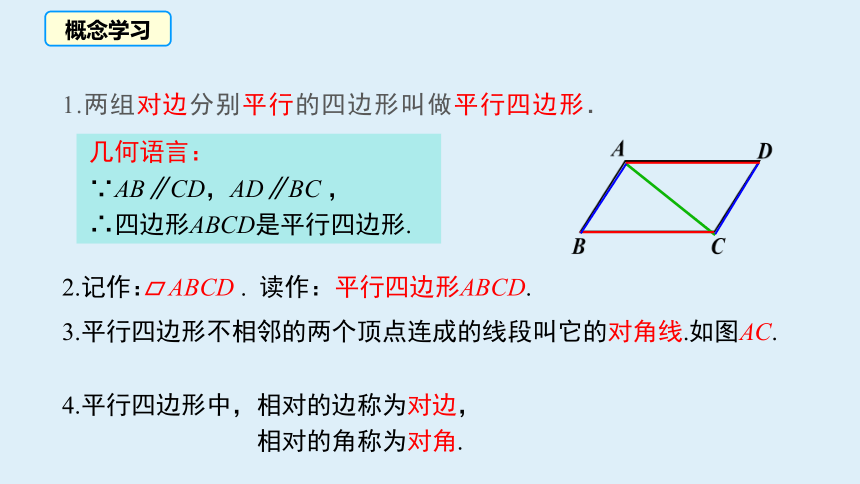
1.两组对边分别平行的四边形叫做平行四边形.
2.记作: ABCD . 读作:平行四边形ABCD.
几何语言:
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
3.平行四边形不相邻的两个顶点连成的线段叫它的对角线.如图AC.
4.平行四边形中,相对的边称为对边,
相对的角称为对角.
概念学习
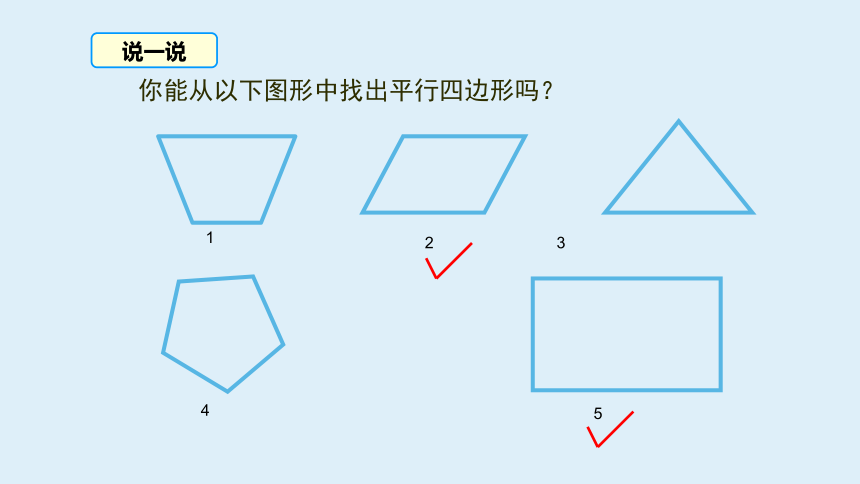
你能从以下图形中找出平行四边形吗?
2
3
1
4
5
说一说
平行四边形边和角的性质
二
平行四边形对边相等,对角相等.
这个结论正确吗?
证明:如图,连接AC,
∵AD∥BC,AB ∥ CD,
∴∠1=∠2,∠3=∠4.
又AC是△ABC和△CDA的公共边,
∴ △ABC≌ △CDA.
∴AB=CD,BC=DA,
∠B=∠D.
已知: ABCD,AB∥CD,AD∥BC.
求证: AB=CD,BC=DA; ∠B=∠D,∠BAD=∠DCB
又∵∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3.
即∠BAD=∠DCB.
证明结论
思考:不添加辅助线,你能否直接 运用平行四边形的定义,证明
其对角相等?
A
B
C
D
证明:∵AB∥DC,
∴∠ABC+∠BCD=180°
∵AD∥BC,
∴∠BAD+∠ABC=180°,
∴∠BCD=∠BAD,
同理 ∠ABC=∠ADC.
例题讲解
例1 已知:如图 ABCD中,BE平分∠ABC交AD于点E。
(1)如果AE=2,求CD的长。
(2)如果∠AEB=40°,求∠C的度数。
A
B
C
D
E
1 .如图,在□ABCD中
(1)若∠A=130°,则∠B=______ ,∠C=______ ,∠D=______.
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
16
当堂练习
2.已知: ABCD,E,F是对角线AC上的两点,并且AE=CF,求证: BE=DF.
证明:∵四边形ABCD是平行四边形,
∴∠BAE=∠DCF.
∴ △ABE≌ △CDF.
∴ AB=CD,AD ∥ BC,
又∵AE=CF,
∴BE=DF.
A
D
B
C
E
F
平行四边形
课堂小结
两组对边分别平行的四边形是平行四边形
定义
性质
对边平行,
对边相等,
对角相等
分层作业:
必做题:教材习题19.1 1,2
选做题:(解决问题)
农民李某想发展副业致 富,经考察地形后,在耕地旁边的荒地上开垦一平行四边形形状的鱼塘。能测得∠B=120° ,量得AD=50米,AB=80米。请你帮助李某计算一下鱼塘的对边AB、CD之间的距离及这个鱼塘的周长。
数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
世界七大数学难题
NP完全问题
霍奇猜想
庞加莱猜想
黎曼假设
杨-米尔斯存在性和质量缺口
纳卫尔-斯托可方程
BSD猜想
悬赏100万美金
在数学课上,老师提出了这样一个问题,用20米的绳子围成平行四边形,且边长是正整数,有多少种围法?小明是个聪明的孩子,很快得出了答案,你知道答案了吗?这时候老师接着提问,如果长边比短边长2米,那将怎样呢
创设情境 1分钟挑战
导入新课
19.2.1 平行四边形
生活中,平行四边形无处不在,那么它有哪些性质呢?今天我们就一起来探讨一下吧!
讲授新课
平行四边形边的相关概念
一
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
平行四边形
活动1:观察图形,说出下列图形边的位置有什么特征?
1.两组对边分别平行的四边形叫做平行四边形.
2.记作: ABCD . 读作:平行四边形ABCD.
几何语言:
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
3.平行四边形不相邻的两个顶点连成的线段叫它的对角线.如图AC.
4.平行四边形中,相对的边称为对边,
相对的角称为对角.
概念学习
你能从以下图形中找出平行四边形吗?
2
3
1
4
5
说一说
平行四边形边和角的性质
二
平行四边形对边相等,对角相等.
这个结论正确吗?
证明:如图,连接AC,
∵AD∥BC,AB ∥ CD,
∴∠1=∠2,∠3=∠4.
又AC是△ABC和△CDA的公共边,
∴ △ABC≌ △CDA.
∴AB=CD,BC=DA,
∠B=∠D.
已知: ABCD,AB∥CD,AD∥BC.
求证: AB=CD,BC=DA; ∠B=∠D,∠BAD=∠DCB
又∵∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3.
即∠BAD=∠DCB.
证明结论
思考:不添加辅助线,你能否直接 运用平行四边形的定义,证明
其对角相等?
A
B
C
D
证明:∵AB∥DC,
∴∠ABC+∠BCD=180°
∵AD∥BC,
∴∠BAD+∠ABC=180°,
∴∠BCD=∠BAD,
同理 ∠ABC=∠ADC.
例题讲解
例1 已知:如图 ABCD中,BE平分∠ABC交AD于点E。
(1)如果AE=2,求CD的长。
(2)如果∠AEB=40°,求∠C的度数。
A
B
C
D
E
1 .如图,在□ABCD中
(1)若∠A=130°,则∠B=______ ,∠C=______ ,∠D=______.
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
16
当堂练习
2.已知: ABCD,E,F是对角线AC上的两点,并且AE=CF,求证: BE=DF.
证明:∵四边形ABCD是平行四边形,
∴∠BAE=∠DCF.
∴ △ABE≌ △CDF.
∴ AB=CD,AD ∥ BC,
又∵AE=CF,
∴BE=DF.
A
D
B
C
E
F
平行四边形
课堂小结
两组对边分别平行的四边形是平行四边形
定义
性质
对边平行,
对边相等,
对角相等
分层作业:
必做题:教材习题19.1 1,2
选做题:(解决问题)
农民李某想发展副业致 富,经考察地形后,在耕地旁边的荒地上开垦一平行四边形形状的鱼塘。能测得∠B=120° ,量得AD=50米,AB=80米。请你帮助李某计算一下鱼塘的对边AB、CD之间的距离及这个鱼塘的周长。
数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
