沪科版数学八年级下册 第17章 一元二次方程 课件(共19张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 第17章 一元二次方程 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 20:04:20 | ||
图片预览






文档简介
(共19张PPT)
第17章 一元二次方程(通用)
1.什么样的方程式一元二次方程?它的一般形式
是什么?
2.一元二次方程的解法有哪些?分别距离说明
3.如何根据一元二次方程的根的判别式来判断方程
是否有实根?
4.一元二次方程的根与系数之间有什么关系?
5.利用一元二次方程模型解决实际问题有哪些步骤?
知识回顾
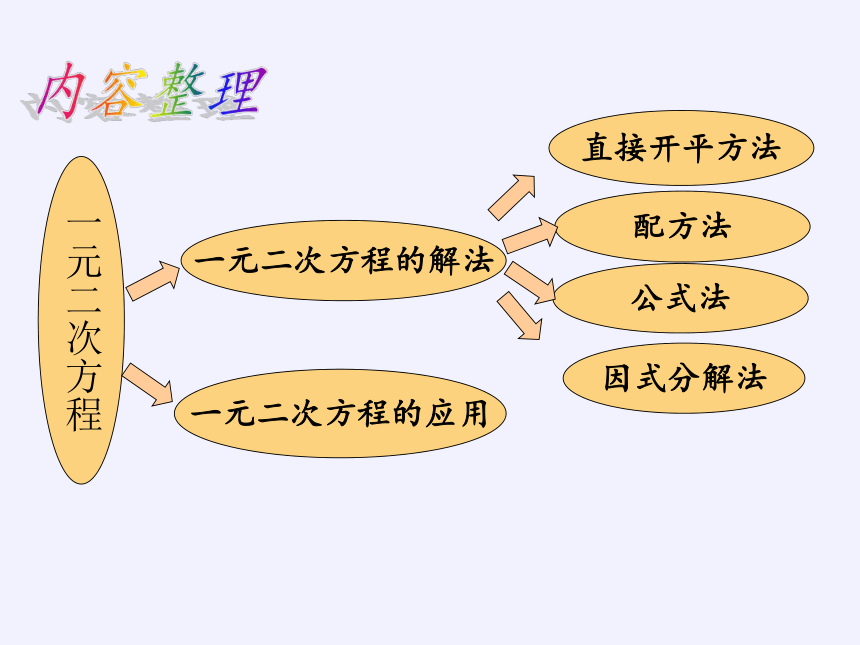
内容整理
一元二次方程的应用
一元二次方程的解法
因式分解法
公式法
配方法
直接开平方法
一元二次方程
1.直接开平方法。
(x+m)2=n(n≥ 0)
2.配方法。
①化——将二次项系数化为1。
③配——在方程两边同时加上一次项系数一半的平
方,使原方程变为(x+m)2=n (n≥ 0)的形式。
④开——用直接开平方法解出方程。
②移——将常数项移到方程的右边。
一元二次方程的解法
3.公式法
4.分解因式法。
求根公式:x= (b2-4ac ≥ 0)
-b±
2a
步骤:①先化为一般形式;
②再确定a、b、c,求b2-4ac;
③当 b2-4ac≥ 0时,代入公式:
④当b2-4ac<0时,方程无实数解
步骤:①右边化为0,左边化成两个因式的积;
②分别令两个因式为0,求解。
1.增长率问题
3.面积体积问题
2.利润问题
4.表格问题
注意: ①设要有单位
②解出方程后检验根的合理性
一元二次方程的应用
1、判断下面哪些方程是一元二次方程
√
√
×
×
×
×
新知探究
2.一元二次方程3+x=2x(x+1)化成一般形式
为 ,其中二次项系数为 。
3.若关于x的方程(m+2)x2-3x-2=0是一元二
次方程,则m的取值范围是 。
2x2+x-3=0
2
m ≠-2
4.解下列方程。
(2x-3)2=9
5.用配方法解方程。
3x2-2x-5=0
6.用公式法解方程。
①x2-2x-3=0
7.用分解因式法解方程。
(4x-1)(5x+7)=0
说出下列方程用哪种方法解比较适当。
(3x-2)2=7
x2-6x-9=0
3x2-2x-1=0
(2x+3)2=(5x+1)2
直接开平方法
配方法
公式法
直接开平方法或分解因式法
1.若一个三位数的个位数字是a,十位
数字是b,百位数字是c,则这个三位数
可表示为 。
100c+10b+a
一元二次方程的应用
2.有一个两位数,它的十位数字与个位数字的和是5.把这个两位数的十位数字与个位数字互换后得到另一个两位数,两个两位数的积为763.求原来的两位数.
3.甲公司前年缴税40万元,今年缴税48.4万元,
若设该公司缴税的年增长率为x,则根据题意可列
方程为 。
2.甲公司前年缴税40万元,去年和今年共缴税95
万元,若设该公司缴税的年增长率为x,则根据题
意可列方程为 。
1.甲公司前年缴税40万元,到今年共缴税135万
元,若设该公司缴税的年增长率为x,则根据题
意可列方程为 。
40(1+x)2=48.4
40(1+x)+40(1+x)2=95
40+40(1+x)+40(1+x)2=135
4. 某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元
解:设每千克水果应涨价x元, 依题意得:
( )( )=6000
10+x
500
解这个方程得:x1=5 , x2=10
要使顾客得到实惠应取x=5
答:每千克水果应涨价 5元.
20x
-
谢 谢
第17章 一元二次方程(通用)
1.什么样的方程式一元二次方程?它的一般形式
是什么?
2.一元二次方程的解法有哪些?分别距离说明
3.如何根据一元二次方程的根的判别式来判断方程
是否有实根?
4.一元二次方程的根与系数之间有什么关系?
5.利用一元二次方程模型解决实际问题有哪些步骤?
知识回顾
内容整理
一元二次方程的应用
一元二次方程的解法
因式分解法
公式法
配方法
直接开平方法
一元二次方程
1.直接开平方法。
(x+m)2=n(n≥ 0)
2.配方法。
①化——将二次项系数化为1。
③配——在方程两边同时加上一次项系数一半的平
方,使原方程变为(x+m)2=n (n≥ 0)的形式。
④开——用直接开平方法解出方程。
②移——将常数项移到方程的右边。
一元二次方程的解法
3.公式法
4.分解因式法。
求根公式:x= (b2-4ac ≥ 0)
-b±
2a
步骤:①先化为一般形式;
②再确定a、b、c,求b2-4ac;
③当 b2-4ac≥ 0时,代入公式:
④当b2-4ac<0时,方程无实数解
步骤:①右边化为0,左边化成两个因式的积;
②分别令两个因式为0,求解。
1.增长率问题
3.面积体积问题
2.利润问题
4.表格问题
注意: ①设要有单位
②解出方程后检验根的合理性
一元二次方程的应用
1、判断下面哪些方程是一元二次方程
√
√
×
×
×
×
新知探究
2.一元二次方程3+x=2x(x+1)化成一般形式
为 ,其中二次项系数为 。
3.若关于x的方程(m+2)x2-3x-2=0是一元二
次方程,则m的取值范围是 。
2x2+x-3=0
2
m ≠-2
4.解下列方程。
(2x-3)2=9
5.用配方法解方程。
3x2-2x-5=0
6.用公式法解方程。
①x2-2x-3=0
7.用分解因式法解方程。
(4x-1)(5x+7)=0
说出下列方程用哪种方法解比较适当。
(3x-2)2=7
x2-6x-9=0
3x2-2x-1=0
(2x+3)2=(5x+1)2
直接开平方法
配方法
公式法
直接开平方法或分解因式法
1.若一个三位数的个位数字是a,十位
数字是b,百位数字是c,则这个三位数
可表示为 。
100c+10b+a
一元二次方程的应用
2.有一个两位数,它的十位数字与个位数字的和是5.把这个两位数的十位数字与个位数字互换后得到另一个两位数,两个两位数的积为763.求原来的两位数.
3.甲公司前年缴税40万元,今年缴税48.4万元,
若设该公司缴税的年增长率为x,则根据题意可列
方程为 。
2.甲公司前年缴税40万元,去年和今年共缴税95
万元,若设该公司缴税的年增长率为x,则根据题
意可列方程为 。
1.甲公司前年缴税40万元,到今年共缴税135万
元,若设该公司缴税的年增长率为x,则根据题
意可列方程为 。
40(1+x)2=48.4
40(1+x)+40(1+x)2=95
40+40(1+x)+40(1+x)2=135
4. 某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元
解:设每千克水果应涨价x元, 依题意得:
( )( )=6000
10+x
500
解这个方程得:x1=5 , x2=10
要使顾客得到实惠应取x=5
答:每千克水果应涨价 5元.
20x
-
谢 谢
