沪科版数学八年级下册 17.3一元二次方程根的判别式 课件(共18张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 17.3一元二次方程根的判别式 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 20:05:38 | ||
图片预览






文档简介
(共18张PPT)
17.3 一 元 二 次 方 程
根 的 判 别 式
用配方法解一元二次方程
想一想
思考:究竟是谁决定了一元二次方程根的情况
式子b2-4ac 叫做一元二次方程ax2+bx+c=0(a≠0)的根的判别式,
通常用符号“Δ”来表示,即Δ= b2-4ac .
4、当Δ = b2-4ac≥0时
方程有
两个实数根
3、当Δ = b2-4ac < 0时,
2、当Δ = b2-4ac = 0时,
1、当Δ = b2-4ac>0时,
方程有
两个不相等的实数根
方程有
方程
两个相等的实数根
无实数根
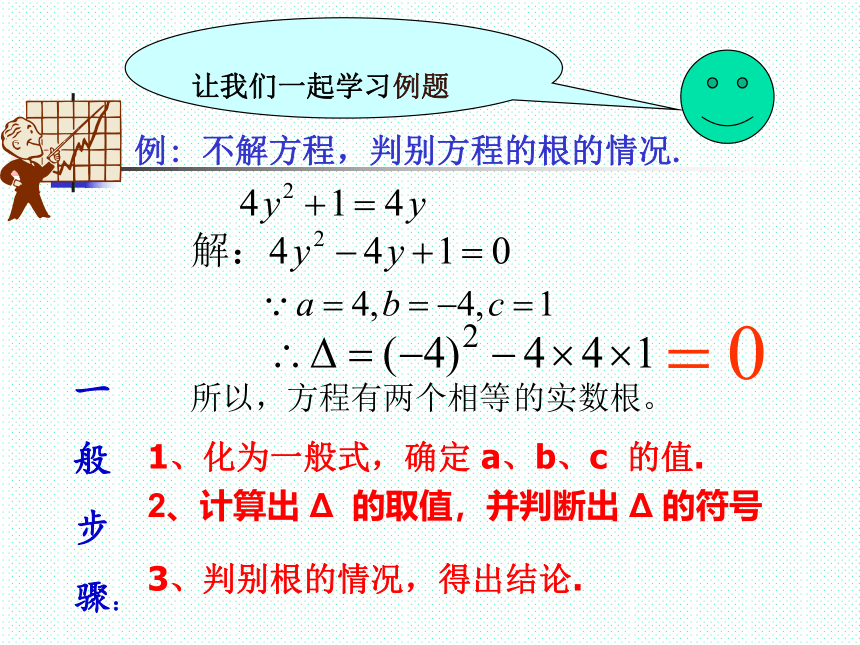
让我们一起学习例题
一
般
步
骤:
3、判别根的情况,得出结论.
例: 不解方程,判别方程的根的情况.
1、化为一般式,确定 a、b、c 的值.
2、计算出 Δ 的取值,并判断出 Δ 的符号
不解方程,判别下列方程的根 的情况。
解:
>0
原方程有两个不相等的实数根。
解:原方程可变形为
原方程有两个相等的实数根。
解:
<0
原方程没有实数根。
看看你做的对不对
例:不解方程,判别关于 的方程
的根的情况.
系数含有字母的方程
1、已知关于x的一元二次方程
mx2-(3m-1)x+2m -2=0(m≠0)
求证:无论m取任何实数时,方程恒有实数根。
所以:无论m取任何实数时,方程恒有实数根。
想一想 你能说出结论1的逆命题吗
结论1:一般地,方程ax2+bx+c=0(a≠0), 当Δ> 0时,有两个不相等的实数根; 当Δ=0时,有两个相等的实数根; 当Δ<0时,没有实数根;
当Δ≤0时, 有两个相等的实数根;
4、当一元二次方程有两个实数根时
3、当方程没有实数根时
2、当方程有两个相等的实数根时
Δ = b2-4ac>0
Δ = b2-4ac < 0
1、当方程有两个不相等的实数根时
Δ = b2-4ac≥0
Δ = b2-4ac = 0
试一试:
(2)解:∵方程有两个相等的实数根
∴Δ= 0 即 (-3)2- 4k = 0, 解得k = k = 时,方程有两个相等的实数根。
关于x的一元二次方程x2-3x + k = 0,
问k取值时
(1)方程有两个不相等的实数根
(2)方程有两个相等的实数根
(3)方程没有实数根
1.(·西宁市)若关于x的一元二次方程mx2-2x+1=0有实数根,则m的取值范围是 ( )
A.m<1 B. m<1且m≠0
C.m≤1 D. m≤1且m≠0
D
2.(·昆明)已知关于x的一元二次方程x2+2x+k=0有实数根,则k的取值范围是 ( )
A.k≤1 B.k≥1 C.k<1 D.k>1
A
3.(·长沙)若一元二次方程 有两个相等的实数根,那么 的值为 ( )
A.-4 B.4 C. 1/4 D.- 1/4
C
.
1、关于 的一元二次方程
m≥0且m≠1
有两个实数根,则m的取值范围为
试一试
2、关于 的一元二次方程
有两个不相等的实数根,则k的取值范围为
课堂总结
Δ = b2-4ac叫做一元二次方程根的判别式。
1.当Δ = b2-4ac>0时
2.当Δ = b2-4ac = 0时
3.当Δ = b2-4ac < 0时
方程有两个不相等的实数根
方程有两个相等的实数根
方程无实数根
注意:当Δ = b2-4ac≥0时
方程有两个实数根
1、在一元二次方程
( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.根的情况无法
A
1、已知关于x的方程
证明:不论m为何值,这个方 程总有两个不相等的实数根
2、已知关于x的方程
(a-2)x2+(-2a+1)x+a=0
有实数根,求a的范围。
17.3 一 元 二 次 方 程
根 的 判 别 式
用配方法解一元二次方程
想一想
思考:究竟是谁决定了一元二次方程根的情况
式子b2-4ac 叫做一元二次方程ax2+bx+c=0(a≠0)的根的判别式,
通常用符号“Δ”来表示,即Δ= b2-4ac .
4、当Δ = b2-4ac≥0时
方程有
两个实数根
3、当Δ = b2-4ac < 0时,
2、当Δ = b2-4ac = 0时,
1、当Δ = b2-4ac>0时,
方程有
两个不相等的实数根
方程有
方程
两个相等的实数根
无实数根
让我们一起学习例题
一
般
步
骤:
3、判别根的情况,得出结论.
例: 不解方程,判别方程的根的情况.
1、化为一般式,确定 a、b、c 的值.
2、计算出 Δ 的取值,并判断出 Δ 的符号
不解方程,判别下列方程的根 的情况。
解:
>0
原方程有两个不相等的实数根。
解:原方程可变形为
原方程有两个相等的实数根。
解:
<0
原方程没有实数根。
看看你做的对不对
例:不解方程,判别关于 的方程
的根的情况.
系数含有字母的方程
1、已知关于x的一元二次方程
mx2-(3m-1)x+2m -2=0(m≠0)
求证:无论m取任何实数时,方程恒有实数根。
所以:无论m取任何实数时,方程恒有实数根。
想一想 你能说出结论1的逆命题吗
结论1:一般地,方程ax2+bx+c=0(a≠0), 当Δ> 0时,有两个不相等的实数根; 当Δ=0时,有两个相等的实数根; 当Δ<0时,没有实数根;
当Δ≤0时, 有两个相等的实数根;
4、当一元二次方程有两个实数根时
3、当方程没有实数根时
2、当方程有两个相等的实数根时
Δ = b2-4ac>0
Δ = b2-4ac < 0
1、当方程有两个不相等的实数根时
Δ = b2-4ac≥0
Δ = b2-4ac = 0
试一试:
(2)解:∵方程有两个相等的实数根
∴Δ= 0 即 (-3)2- 4k = 0, 解得k = k = 时,方程有两个相等的实数根。
关于x的一元二次方程x2-3x + k = 0,
问k取值时
(1)方程有两个不相等的实数根
(2)方程有两个相等的实数根
(3)方程没有实数根
1.(·西宁市)若关于x的一元二次方程mx2-2x+1=0有实数根,则m的取值范围是 ( )
A.m<1 B. m<1且m≠0
C.m≤1 D. m≤1且m≠0
D
2.(·昆明)已知关于x的一元二次方程x2+2x+k=0有实数根,则k的取值范围是 ( )
A.k≤1 B.k≥1 C.k<1 D.k>1
A
3.(·长沙)若一元二次方程 有两个相等的实数根,那么 的值为 ( )
A.-4 B.4 C. 1/4 D.- 1/4
C
.
1、关于 的一元二次方程
m≥0且m≠1
有两个实数根,则m的取值范围为
试一试
2、关于 的一元二次方程
有两个不相等的实数根,则k的取值范围为
课堂总结
Δ = b2-4ac叫做一元二次方程根的判别式。
1.当Δ = b2-4ac>0时
2.当Δ = b2-4ac = 0时
3.当Δ = b2-4ac < 0时
方程有两个不相等的实数根
方程有两个相等的实数根
方程无实数根
注意:当Δ = b2-4ac≥0时
方程有两个实数根
1、在一元二次方程
( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.根的情况无法
A
1、已知关于x的方程
证明:不论m为何值,这个方 程总有两个不相等的实数根
2、已知关于x的方程
(a-2)x2+(-2a+1)x+a=0
有实数根,求a的范围。
