冀教版数学七年级下册同步课件:7.1 第2课时 说理(共19张PPT)
文档属性
| 名称 | 冀教版数学七年级下册同步课件:7.1 第2课时 说理(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 275.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 10:14:49 | ||
图片预览




文档简介
(共19张PPT)
第七章 相交线与平行线
7.1 第2课时 说理
知识回顾
问题1 什么叫做命题?命题有哪些部分组成?有哪些类型?
能够进行肯定或者否定判断的语句,叫做命题.
一般地,命题都是由条件和结论两部分组成的.
在命题中,既有正确的命题,也有不正确的命题.我们把正确的命题叫做真命题,把不正确的命题叫做假命题.
要说明一个命题是假命题,只要举出一个符合命题条件,但不符合命题结论的例子就可以,像这样的例子叫做反例.
问题2 什么叫做反例?
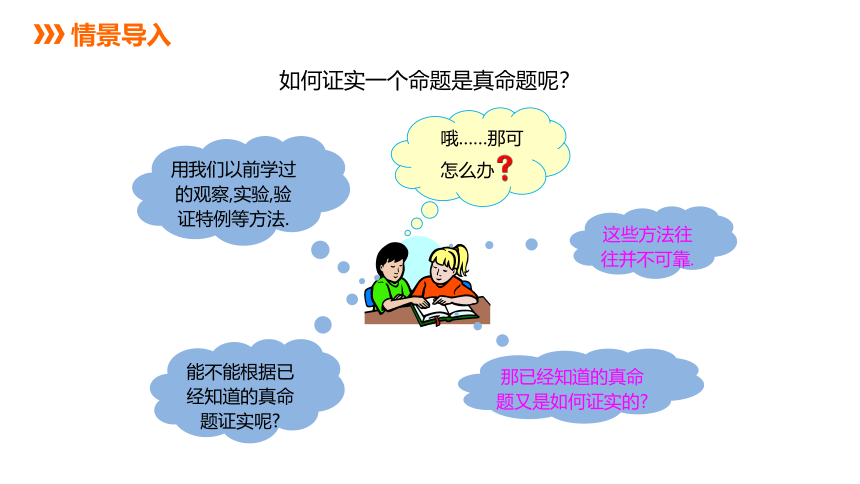
如何证实一个命题是真命题呢?
用我们以前学过的观察,实验,验证特例等方法.
这些方法往往并不可靠.
那已经知道的真命题又是如何证实的
能不能根据已经知道的真命题证实呢
哦……那可
怎么办
情景导入
观察与思考
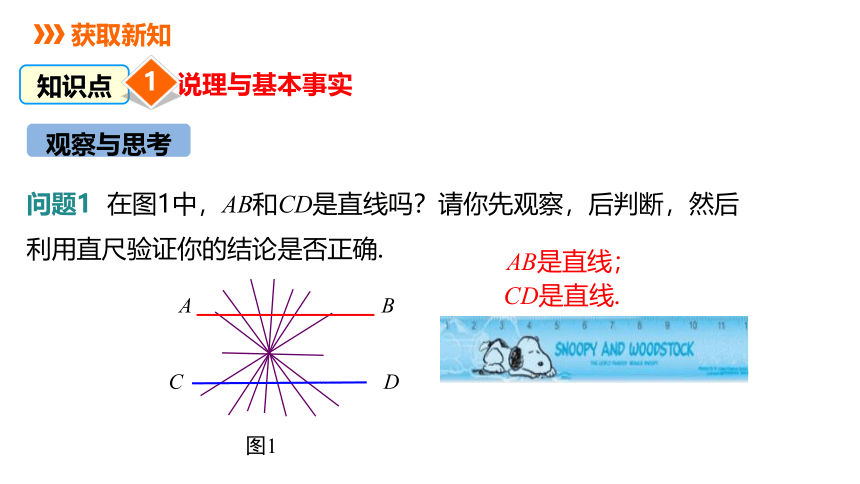
问题1 在图1中,AB和CD是直线吗?请你先观察,后判断,然后利用直尺验证你的结论是否正确.
图1
A
B
C
D
AB是直线;
CD是直线.
获取新知
知识点
说理与基本事实
1
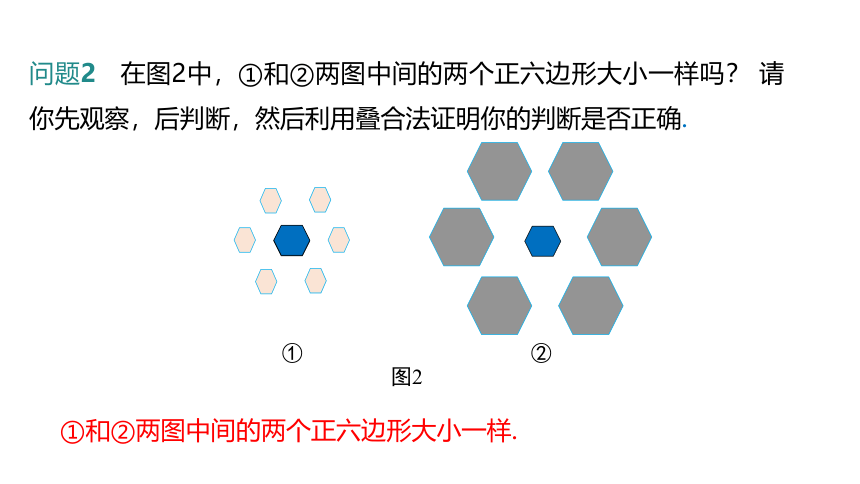
问题2 在图2中,①和②两图中间的两个正六边形大小一样吗? 请你先观察,后判断,然后利用叠合法证明你的判断是否正确.
图2
①
②
①和②两图中间的两个正六边形大小一样.
问题3 如果a=-b,那么a2=b2.由此得出:当a=-b时,a3=b3.你认为后一个命题正确吗?为什么?
后一个命题不正确.
说明:设a=1,b=-1,则a=-b.(符合命题的条件)
则a3=13=1,b3=(-1)3=-1,则a3≠b3.(不符合命题的结论)
所以命题“当a=-b时,a3=b3”是个假命题.
知识要点
由观察、实验、归纳和类比等方法得出的命题,可能是真命题,也可能是假命题.判断命题的真假需要说明理由,这个过程就是说理.
有些命题经过实践经验被公认为真命题,我们把这样的命题叫做基本事实.
我们学过的基本事实有哪些呢?
过平面上两点,有且只有一条直线.
两点之间的连线中,垂线最短.
互动探究
观察相邻两个奇数的和:
1
3
5
7
9
···
4
8
12
16
···
问题1 相邻两个奇数的和与4之间有什么关系?请提出你的猜想.
相邻两个奇数的和都能被4的整除.
实验、归纳是常用的发现命题的方法.
知识点
定理与演绎推理
2
问题2 通过说理,验证你的猜想正确与否.
说明:设a=2k-1,b=2k+1,其中k是整数.(符合命题的条件)
则a+b=2k-1+(2k+1)=4k.(符合命题的结论)
所以“相邻两个奇数的和能被4整除”这个命题是真命题.
两个相邻偶数的和与4能被4整除,这个命题是真命题吗?
说明:设a=2k,b=2k+2,其中k是整数.(符合命题的条件)
则a+b=2k+(2k+2)=4k+2.(不符合命题的结论)
所以“两个相邻偶数的和与4能被4整除”这个命题是假命题.
想一想:与一个偶数前后相邻的两个偶数之和,一定是4的倍数,这个命题是真命题吗?
例 如图,说明“如果C,D是线段AB上的两点,且AC=BD,那么AD=CB”是真命题.
A
C
D
B
理由:因为 AC=DB(已知),
所以 AC+CD=DB+CD(等量加等量,和相等),
所以 AD=CB(线段和的定义).
例题讲解
知识要点
依据已有的事实(包括定义、基本事实、已被确认的真命题),按照确定的规则,得到某个具体的结论的推理就是演绎推理.
有些真命题,它们的正确性已经过演绎推理得到证实,并被作为判定其他命题真假的依据,这些命题叫做定理.
练一练
说明“如果∠A和∠B都是∠C的补角,那么∠A=∠B”是一个真命题.
理由:因为∠A+∠C=180°.(补角的定义),
所以 ∠A=180°-∠C (等式的性质).
因为 ∠B+∠C=180° (补角的定义),
所以 ∠B=180°-∠C (等式的性质),
所以 ∠A=∠C ( 等量代换 ).
1.下列问题用到推理的是( )
A.根据a=10,b=10,得到a=b
B.观察得到了三角形有三个角
C.老师告诉了我们关于金字塔的许多奥秘
D.由经验可知过两点有且只有一条直线
A
随堂演练
2.下列说法中不正确的是( )
A.证实命题正确与否的推理过程就是说理
B.命题是判断一件事的语句
C.基本事实的正确与否必须通过推理的方法来证实
D.定理都是真命题,但真命题不一定是定理
C
3.如图,已知线段AB,点C,M都是线段AB上的点,若M是BC的中点,则AC+AB=2AM,请在下面说理过程的括号内填写适当的说明依据.
A
C
M
B
理由:因为M是BC的中点(已知),
所以 BC=2MC ( ).
因为 AM=AC+CM ( ),
线段中点的定义
线段和的定义
所以 2AM=2AC+2CM ( ),
等式的性质2
所以 2AM=2AC+BC ( ),
等量代换
又因为 AB=AC+BC ( ),
线段和的定义
所以 2AM=AC+BC ( ),
等量代换
4.如图所示,OM为∠AOB内的任意一条射线,OE,OF分别是∠AOM和∠BOM的平分线, 那么∠AOB=2∠EOF.请在下面说理过程的括号内填上推理的依据.
O
A
B
M
E
F
理由:因为OE平分∠AOM( ),
所以 ∠AOM=2∠EOM ( ).
角平分线的定义
所以 ∠BOM=2∠FOM( ).
角平分线的定义
已知
因为OF平分∠BOM( ),
已知
因为 ∠AOB=∠AOM+∠BOM ( ).
所以 ∠AOB=2∠EOM+2∠FOM ( ).
所以 ∠AOB=2∠EOF ( ).
角的和的定义
等量代换
角的和的定义
说理
演绎推理
基本事实
定理
课堂小结
第七章 相交线与平行线
7.1 第2课时 说理
知识回顾
问题1 什么叫做命题?命题有哪些部分组成?有哪些类型?
能够进行肯定或者否定判断的语句,叫做命题.
一般地,命题都是由条件和结论两部分组成的.
在命题中,既有正确的命题,也有不正确的命题.我们把正确的命题叫做真命题,把不正确的命题叫做假命题.
要说明一个命题是假命题,只要举出一个符合命题条件,但不符合命题结论的例子就可以,像这样的例子叫做反例.
问题2 什么叫做反例?
如何证实一个命题是真命题呢?
用我们以前学过的观察,实验,验证特例等方法.
这些方法往往并不可靠.
那已经知道的真命题又是如何证实的
能不能根据已经知道的真命题证实呢
哦……那可
怎么办
情景导入
观察与思考
问题1 在图1中,AB和CD是直线吗?请你先观察,后判断,然后利用直尺验证你的结论是否正确.
图1
A
B
C
D
AB是直线;
CD是直线.
获取新知
知识点
说理与基本事实
1
问题2 在图2中,①和②两图中间的两个正六边形大小一样吗? 请你先观察,后判断,然后利用叠合法证明你的判断是否正确.
图2
①
②
①和②两图中间的两个正六边形大小一样.
问题3 如果a=-b,那么a2=b2.由此得出:当a=-b时,a3=b3.你认为后一个命题正确吗?为什么?
后一个命题不正确.
说明:设a=1,b=-1,则a=-b.(符合命题的条件)
则a3=13=1,b3=(-1)3=-1,则a3≠b3.(不符合命题的结论)
所以命题“当a=-b时,a3=b3”是个假命题.
知识要点
由观察、实验、归纳和类比等方法得出的命题,可能是真命题,也可能是假命题.判断命题的真假需要说明理由,这个过程就是说理.
有些命题经过实践经验被公认为真命题,我们把这样的命题叫做基本事实.
我们学过的基本事实有哪些呢?
过平面上两点,有且只有一条直线.
两点之间的连线中,垂线最短.
互动探究
观察相邻两个奇数的和:
1
3
5
7
9
···
4
8
12
16
···
问题1 相邻两个奇数的和与4之间有什么关系?请提出你的猜想.
相邻两个奇数的和都能被4的整除.
实验、归纳是常用的发现命题的方法.
知识点
定理与演绎推理
2
问题2 通过说理,验证你的猜想正确与否.
说明:设a=2k-1,b=2k+1,其中k是整数.(符合命题的条件)
则a+b=2k-1+(2k+1)=4k.(符合命题的结论)
所以“相邻两个奇数的和能被4整除”这个命题是真命题.
两个相邻偶数的和与4能被4整除,这个命题是真命题吗?
说明:设a=2k,b=2k+2,其中k是整数.(符合命题的条件)
则a+b=2k+(2k+2)=4k+2.(不符合命题的结论)
所以“两个相邻偶数的和与4能被4整除”这个命题是假命题.
想一想:与一个偶数前后相邻的两个偶数之和,一定是4的倍数,这个命题是真命题吗?
例 如图,说明“如果C,D是线段AB上的两点,且AC=BD,那么AD=CB”是真命题.
A
C
D
B
理由:因为 AC=DB(已知),
所以 AC+CD=DB+CD(等量加等量,和相等),
所以 AD=CB(线段和的定义).
例题讲解
知识要点
依据已有的事实(包括定义、基本事实、已被确认的真命题),按照确定的规则,得到某个具体的结论的推理就是演绎推理.
有些真命题,它们的正确性已经过演绎推理得到证实,并被作为判定其他命题真假的依据,这些命题叫做定理.
练一练
说明“如果∠A和∠B都是∠C的补角,那么∠A=∠B”是一个真命题.
理由:因为∠A+∠C=180°.(补角的定义),
所以 ∠A=180°-∠C (等式的性质).
因为 ∠B+∠C=180° (补角的定义),
所以 ∠B=180°-∠C (等式的性质),
所以 ∠A=∠C ( 等量代换 ).
1.下列问题用到推理的是( )
A.根据a=10,b=10,得到a=b
B.观察得到了三角形有三个角
C.老师告诉了我们关于金字塔的许多奥秘
D.由经验可知过两点有且只有一条直线
A
随堂演练
2.下列说法中不正确的是( )
A.证实命题正确与否的推理过程就是说理
B.命题是判断一件事的语句
C.基本事实的正确与否必须通过推理的方法来证实
D.定理都是真命题,但真命题不一定是定理
C
3.如图,已知线段AB,点C,M都是线段AB上的点,若M是BC的中点,则AC+AB=2AM,请在下面说理过程的括号内填写适当的说明依据.
A
C
M
B
理由:因为M是BC的中点(已知),
所以 BC=2MC ( ).
因为 AM=AC+CM ( ),
线段中点的定义
线段和的定义
所以 2AM=2AC+2CM ( ),
等式的性质2
所以 2AM=2AC+BC ( ),
等量代换
又因为 AB=AC+BC ( ),
线段和的定义
所以 2AM=AC+BC ( ),
等量代换
4.如图所示,OM为∠AOB内的任意一条射线,OE,OF分别是∠AOM和∠BOM的平分线, 那么∠AOB=2∠EOF.请在下面说理过程的括号内填上推理的依据.
O
A
B
M
E
F
理由:因为OE平分∠AOM( ),
所以 ∠AOM=2∠EOM ( ).
角平分线的定义
所以 ∠BOM=2∠FOM( ).
角平分线的定义
已知
因为OF平分∠BOM( ),
已知
因为 ∠AOB=∠AOM+∠BOM ( ).
所以 ∠AOB=2∠EOM+2∠FOM ( ).
所以 ∠AOB=2∠EOF ( ).
角的和的定义
等量代换
角的和的定义
说理
演绎推理
基本事实
定理
课堂小结
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
