冀教版数学七年级下册同步课件:6.3.2二元一次方程组的应用(二)(共24张PPT)
文档属性
| 名称 | 冀教版数学七年级下册同步课件:6.3.2二元一次方程组的应用(二)(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 20:35:43 | ||
图片预览








文档简介
(共24张PPT)
第六章 二元一次方程组
6.3 第2课时 二元一次方程组的应用(二)
列二元一次方程组解应用题的一般步骤是什么?
审
设
列
解
答
根据相等关系列出需要的代数式,并列出方程
弄清题意和题中的已知量、未知量等
用字母表示问题中的2个未知数
解这个方程组,求出未知数的值
写出答案
知识回顾
找
找出2个相等关系
例1 去年秋季,某校七年级和高一年级招生总人数为500人,计划今年秋季七年级招生人数增加20%,高中一年级人数增加15%,这样,今年秋季七年级和高中一年级招生总人数将比去年增加18%,今年秋季七年级和高中一年级各计划招生多少人?
今年,七年级人数+高中一年级人数=500(1+18%);
分析:本题中的等量关系
去年,七年级人数+高中一年级人数=500;
今年,七年级人数=去年七年级人数+增长数;
今年,高中一年级人数=去年高中一年级人数+增长数;
例题讲解
知识点
百分率问题
1
解:设去年七年级招生x名,高中一年级招生y名.根据题意,得
解得
所以
答:今年秋季七年级计划招生360名,高中一年级计划招生230名.
如果将今年两个年级计划招生人数设为未知数,如何列方程组呢?
基本关系式:
增长率=(增长后的量-增长前的量)/增长前的量×100%;
相等关系:
增长前的量×(1+增长率) =增长后的量;
下降前的量×(1-降低率) =下降后的量.
归纳
【分析】设去年的总产值为x万元,总支出为y万元,则有
总产值/万元 总支出/万元 利润/万元
去年
今年
(1+20﹪)x
(1-10﹪)y
780
x
y
200
某工厂去年的利润(总产值-总支出)为200万元,今年总产值比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元.去年的总产值、总支出各是多少万元
变式练习
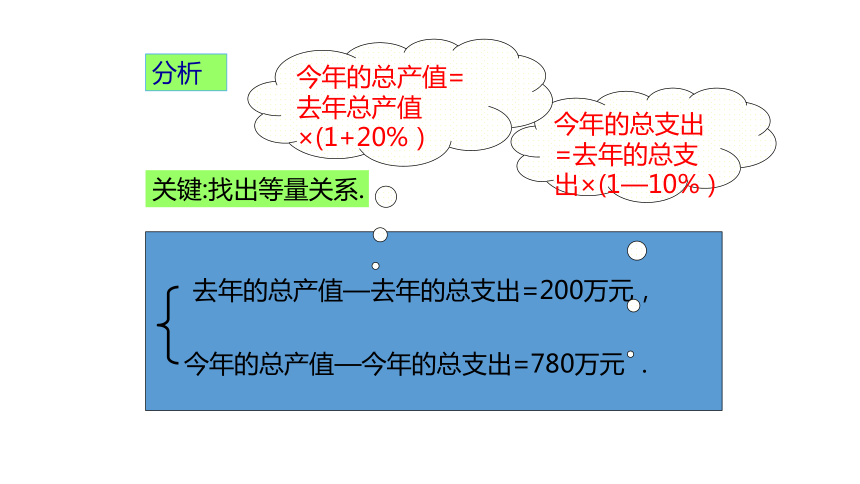
去年的总产值—去年的总支出=200万元,
今年的总产值—今年的总支出=780万元 .
分析
关键:找出等量关系.
今年的总支出=去年的总支出×(1—10%)
今年的总产值=
去年总产值×(1+20%)
解:设去年的总产值为x万元,总支出为y万元,则有
x-y=200
(1+20﹪)x-(1-10﹪)y=780
因此,去年的总产值是2 000万元,总支出是1800万元.
解得
x=2 000
y=1 800
例2 小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
例题讲解
知识点
行程问题
2
分析:小华到学校的路分成两段,一段为平路,一段为下坡路.
平路:60 m/min
下坡路:80 m/min
上坡路:40 m/min
走平路的时间+走下坡的时间=________,
走上坡的时间+走平路的时间= _______.
路程=平均速度×时间
10
15
方法一(直接设元法)
平路时间 坡路时间 总时间
上学
放学
解:设小华家到学校平路长x m,下坡长y m.
根据题意,可列方程组:
解方程组,得
所以,小明家到学校的距离为700米.
方法二(间接设元法)
平路 距离 坡路距离
上学
放学
解:设小华下坡路所花时间为x min,上坡路所花时间为y min.
根据题意,可列方程组:
解方程组,得
所以,小明家到学校的距离为700米.
故 平路距离:60×(10-5)=300(米)
坡路距离:80×5=400(米)
甲、乙两地相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
分析:对于行程问题,一般可以借助示意图表示题中的数量关系,可以更加直观的找到相等关系.
变式练习
(1) 同时出发,同向而行
甲出发点
乙出发点
4km
甲追上乙
乙2h行程
甲2h行程
甲2h行程=4km+乙2h行程
(2) 同时出发,相向而行
甲出发点
乙出发点
4km
相遇地
甲0.5h
行程
乙0.5h
行程
甲0.5h行程+乙0.5h行程=4km
解:设甲、乙的速度分别为x km/h,y km/h.根据题意与分析中图示的两个相等关系,得
解方程组,得
答:甲的速度为5 km/h,乙的速度为3 km/h.
小明为了测得火车过桥时的速度和火车的长度,在一铁路桥旁进行观察,火车从开始上桥到完全过桥共用26s, 整列火车完全在桥上的时间为14s. 已知桥长1000m,你能根据小明测得的数据求出火车的速度和长度吗
思考:(1)问题中涉及了哪些量?
(2)画示意图,并寻找等量关系.
(3)用x、y分别表示火车的速度(m/s) 和长度(m), 列方程组.
(4)解答上面的问题.
一起探究
小明为了测得火车过桥时的速度和火车的长度,在一铁路桥旁进行观察,火车从开始上桥到完全过桥共用26s, 整列火车完全在桥上的时间为14s. 已知桥长1000m,你能根据小明测得的数据求出火车的速度和长度吗
火车26s内所行路程=桥长+火车长
火车14s内所行路程=桥长-火车长
解:设火车的速度为x m/s,长度为y m.
根据题意,得
26x=1000+y
14x=1000-y
x=50
y=300
解得
答:火车的速度为50 m/s,长度为300m.
实际问题
设未知数、找等量关系、列方程(组)
数学问题
[方程(组)]
解方程(组)
数学问题的解
检 验
实际问题
的答案
归纳
1.甲、乙两人赛跑,若乙先跑10米,甲跑5秒即可追上乙;若乙先跑2秒,则甲跑4秒就可追上乙.设甲速为x米/秒,乙速为y米/秒,则可列方程组为( ).
B
4y=6x
4x=6y
4y=6x
5y+10=5x,
5x=5y+10,
5x+10=5y,
4x=6y
5y=5x+10,
A
B
C
D
{
{
{
{
随堂演练
2. 甲、乙两种商品原来的单价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.求甲、乙两种商品原来的单价.
解: 设甲商品原来的单价为x 元,乙商品原来的单价为y 元.
根据等量关系得
解这个方程组得
答:甲商品原来的单价为40元,乙商品原来的单价为60元.
3.某业余运动员针对自行车和长跑项目进行专项训练某次训练中,他骑自行车的平均速度为10 m/s,跑步的平均速度为 ,自行车路段和长跑路段共5 km,共用时15 min.求自行车路段和长跑路段的长度.
分析:本问题涉及的等量关系有:
自行车路段长度+长跑路段长度=总路程,
骑自行车的时间+长跑时间=总时间.
解: 设自行车路段的长度为x m,长跑路段的长度为y m.
根据等量关系,得
解这个方程组,得
因此自行车路段的长度为3000m,
长跑路段的长度为2000m.
课堂小结
列方程组解决问题
一般步骤:
审、找、设、列、解、验、答
关键:找等量关系
第六章 二元一次方程组
6.3 第2课时 二元一次方程组的应用(二)
列二元一次方程组解应用题的一般步骤是什么?
审
设
列
解
答
根据相等关系列出需要的代数式,并列出方程
弄清题意和题中的已知量、未知量等
用字母表示问题中的2个未知数
解这个方程组,求出未知数的值
写出答案
知识回顾
找
找出2个相等关系
例1 去年秋季,某校七年级和高一年级招生总人数为500人,计划今年秋季七年级招生人数增加20%,高中一年级人数增加15%,这样,今年秋季七年级和高中一年级招生总人数将比去年增加18%,今年秋季七年级和高中一年级各计划招生多少人?
今年,七年级人数+高中一年级人数=500(1+18%);
分析:本题中的等量关系
去年,七年级人数+高中一年级人数=500;
今年,七年级人数=去年七年级人数+增长数;
今年,高中一年级人数=去年高中一年级人数+增长数;
例题讲解
知识点
百分率问题
1
解:设去年七年级招生x名,高中一年级招生y名.根据题意,得
解得
所以
答:今年秋季七年级计划招生360名,高中一年级计划招生230名.
如果将今年两个年级计划招生人数设为未知数,如何列方程组呢?
基本关系式:
增长率=(增长后的量-增长前的量)/增长前的量×100%;
相等关系:
增长前的量×(1+增长率) =增长后的量;
下降前的量×(1-降低率) =下降后的量.
归纳
【分析】设去年的总产值为x万元,总支出为y万元,则有
总产值/万元 总支出/万元 利润/万元
去年
今年
(1+20﹪)x
(1-10﹪)y
780
x
y
200
某工厂去年的利润(总产值-总支出)为200万元,今年总产值比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元.去年的总产值、总支出各是多少万元
变式练习
去年的总产值—去年的总支出=200万元,
今年的总产值—今年的总支出=780万元 .
分析
关键:找出等量关系.
今年的总支出=去年的总支出×(1—10%)
今年的总产值=
去年总产值×(1+20%)
解:设去年的总产值为x万元,总支出为y万元,则有
x-y=200
(1+20﹪)x-(1-10﹪)y=780
因此,去年的总产值是2 000万元,总支出是1800万元.
解得
x=2 000
y=1 800
例2 小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
例题讲解
知识点
行程问题
2
分析:小华到学校的路分成两段,一段为平路,一段为下坡路.
平路:60 m/min
下坡路:80 m/min
上坡路:40 m/min
走平路的时间+走下坡的时间=________,
走上坡的时间+走平路的时间= _______.
路程=平均速度×时间
10
15
方法一(直接设元法)
平路时间 坡路时间 总时间
上学
放学
解:设小华家到学校平路长x m,下坡长y m.
根据题意,可列方程组:
解方程组,得
所以,小明家到学校的距离为700米.
方法二(间接设元法)
平路 距离 坡路距离
上学
放学
解:设小华下坡路所花时间为x min,上坡路所花时间为y min.
根据题意,可列方程组:
解方程组,得
所以,小明家到学校的距离为700米.
故 平路距离:60×(10-5)=300(米)
坡路距离:80×5=400(米)
甲、乙两地相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
分析:对于行程问题,一般可以借助示意图表示题中的数量关系,可以更加直观的找到相等关系.
变式练习
(1) 同时出发,同向而行
甲出发点
乙出发点
4km
甲追上乙
乙2h行程
甲2h行程
甲2h行程=4km+乙2h行程
(2) 同时出发,相向而行
甲出发点
乙出发点
4km
相遇地
甲0.5h
行程
乙0.5h
行程
甲0.5h行程+乙0.5h行程=4km
解:设甲、乙的速度分别为x km/h,y km/h.根据题意与分析中图示的两个相等关系,得
解方程组,得
答:甲的速度为5 km/h,乙的速度为3 km/h.
小明为了测得火车过桥时的速度和火车的长度,在一铁路桥旁进行观察,火车从开始上桥到完全过桥共用26s, 整列火车完全在桥上的时间为14s. 已知桥长1000m,你能根据小明测得的数据求出火车的速度和长度吗
思考:(1)问题中涉及了哪些量?
(2)画示意图,并寻找等量关系.
(3)用x、y分别表示火车的速度(m/s) 和长度(m), 列方程组.
(4)解答上面的问题.
一起探究
小明为了测得火车过桥时的速度和火车的长度,在一铁路桥旁进行观察,火车从开始上桥到完全过桥共用26s, 整列火车完全在桥上的时间为14s. 已知桥长1000m,你能根据小明测得的数据求出火车的速度和长度吗
火车26s内所行路程=桥长+火车长
火车14s内所行路程=桥长-火车长
解:设火车的速度为x m/s,长度为y m.
根据题意,得
26x=1000+y
14x=1000-y
x=50
y=300
解得
答:火车的速度为50 m/s,长度为300m.
实际问题
设未知数、找等量关系、列方程(组)
数学问题
[方程(组)]
解方程(组)
数学问题的解
检 验
实际问题
的答案
归纳
1.甲、乙两人赛跑,若乙先跑10米,甲跑5秒即可追上乙;若乙先跑2秒,则甲跑4秒就可追上乙.设甲速为x米/秒,乙速为y米/秒,则可列方程组为( ).
B
4y=6x
4x=6y
4y=6x
5y+10=5x,
5x=5y+10,
5x+10=5y,
4x=6y
5y=5x+10,
A
B
C
D
{
{
{
{
随堂演练
2. 甲、乙两种商品原来的单价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.求甲、乙两种商品原来的单价.
解: 设甲商品原来的单价为x 元,乙商品原来的单价为y 元.
根据等量关系得
解这个方程组得
答:甲商品原来的单价为40元,乙商品原来的单价为60元.
3.某业余运动员针对自行车和长跑项目进行专项训练某次训练中,他骑自行车的平均速度为10 m/s,跑步的平均速度为 ,自行车路段和长跑路段共5 km,共用时15 min.求自行车路段和长跑路段的长度.
分析:本问题涉及的等量关系有:
自行车路段长度+长跑路段长度=总路程,
骑自行车的时间+长跑时间=总时间.
解: 设自行车路段的长度为x m,长跑路段的长度为y m.
根据等量关系,得
解这个方程组,得
因此自行车路段的长度为3000m,
长跑路段的长度为2000m.
课堂小结
列方程组解决问题
一般步骤:
审、找、设、列、解、验、答
关键:找等量关系
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
