冀教版数学七年级下册同步课件:8.5 第1课时 平方差公式(共17张PPT)
文档属性
| 名称 | 冀教版数学七年级下册同步课件:8.5 第1课时 平方差公式(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 241.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 21:20:18 | ||
图片预览





文档简介
(共17张PPT)
第八章 整式的乘法
8.5 第1课时 平方差公式
知识回顾
多项式与多项式是如何相乘的?
(x + 3)( x+5)
=x2
+5x
+3x
+15
=x2
+8x
+15.
(a+b)(m+n)
=am
+an
+bm
+bn
情景导入
“灰太狼的阴谋”?
灰太狼开起了租地公司,他把一块边长
为a米的正方形土地租给慢羊羊种植.有一年他对慢羊羊说:“我把这块地的一边增加5米,另一边减少5米,再继续租给你, 你也没吃亏,你看如何 ”慢羊羊一听觉得没有吃亏,就答应了.回到羊村,就把这件事对喜羊羊他们讲了,喜羊羊一听,就说道:“村长,您吃亏了!” 慢羊羊村长很吃惊…
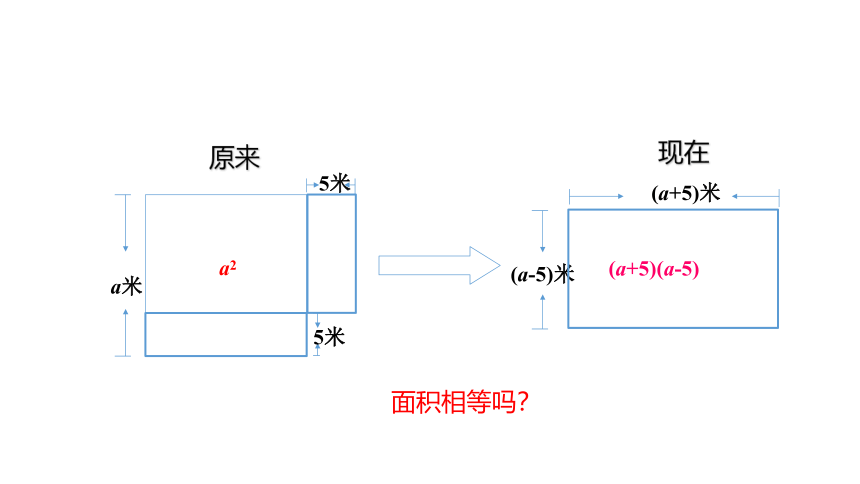
同学们,你认为慢羊羊吃亏了吗?
5米
5米
a米
(a-5)米
(a+5)米
面积相等吗?
原来
现在
a2
(a+5)(a-5)
获取新知
①(x + 1)( x-1);
②(m + 2)( m-2);
③(2m+ 1)(2m-1);
④(5y + z)(5y-z).
问题1:计算下列多项式的积,你能发现什么规律?
x2 - 12
m2-22
(2m)2 - 12
(5y)2 - z2
想一想:这些计算结果有什么共同特点?
知识点
平方差的特征
1
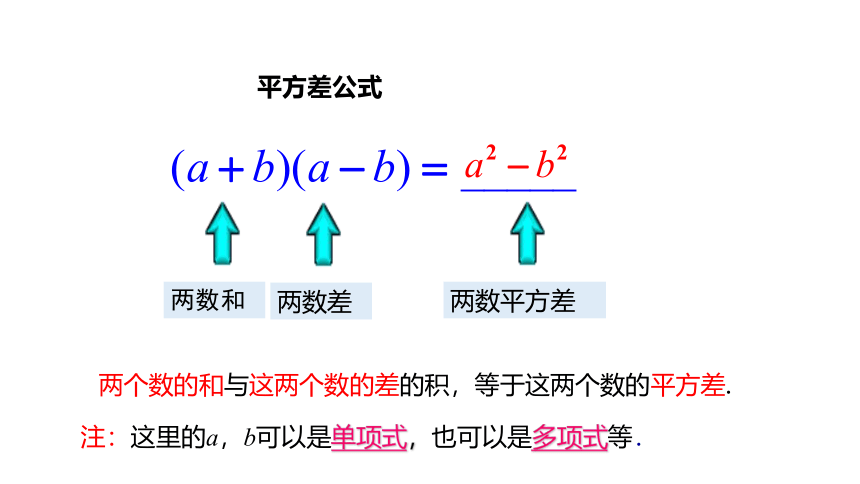
两数和
两数差
两数平方差
两个数的和与这两个数的差的积,等于这两个数的平方差.
平方差公式
注:这里的a,b可以是单项式,也可以是多项式等.
左边=
=右边
代数验证
(多项式乘以多项式的法则)
(合并同类项法则)
问题2
如图,在一个边长为a的正方形中,剪去一个边长为b的小正方形,再将余下的部分剪拼成一个长方形.
(1)两个图形(着色部分)的面积之间有什么关系?
(2)请你结合图形对平方差公式(a+b)(a-b)=a2-b2进行解释.
b
a
图1
相等
图1:a2-b2
图2:长:(a+b),宽:(a-b)
面积:(a+b)(a-b)
b
a
图2
b
a2-b2=(a+b)(a-b)
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
a-b
a-b
几何验证
面积法
算式 与平方差公式中a对应的项 与平方差公式中b对应的项 写成“a2-b2”的形式 计算结果
(m+2)(m-2)
(2m+3)(2m-3)
(x+2y)(-x+2y)
(1+3y)(1-3y)
问题3
按要求填写下面的表格:
m
2
m2-22
m2-4
2m
3
(2m)2-32
4m2-9
2y
x
(2y)2-x2
4y2-x2
1
3y
12-(3y)2
1-9y2
知识点
平方差公式的运用
2
例题讲解
例1 计算:
a
b
解:
利用平方差公式计算,必须找到相同的项和互为相反数的项
a
b
a
b
例2 用平方差公式计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .
解: (1) 102×98
(2) (y+2)(y-2)- (y-1)(y+5)
= 1002-22
=10000 – 4
=(100+2)(100-2)
=9996
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.
1.下列各式中,能用平方差公式运算的是( )
A.(-a+b)(-a-b) B.(a-b)(b-a)
C.(2a-3b)(3a+2b) D .(-2y-x)(x+2y)
A
随堂演练
2.计算(2x+3)(2x-3)的值是( )
A.4x2-9 B.4x2-3
C.2x2-9 D.2x2-3
A
3.计算:
(1)(x+1)(x-____)=x2-1;
(2)(x+3y)______=9y2-x2.
(3y-x)
1
4.下面各式的计算对不对?如果不对,应当怎样改正?
(1)(x+2)(x-2)=x2-2
(2)(-3a-2)(3a-2)=9a2-4
不对
改正:
(1)(x+2)(x-2)=x2-4
不对
改正方法1:
(-3a-2)(3a-2)=-[(3a+2)(3a-2)]=-(9a2-4)=-9a2+4.
改正方法2:
(-3a-2)(3a-2)=(-2-3a)(-2+3a)=(-2)2-(3a)2=4-9a2
(1)(a+3b)(a- 3b);
=4a2-9;
=4x4-y2;
原式=(2a+3)(2a-3)
=a2-9b2 ;
=(2a)2-32
原式=(-2x2 )2-y2
原式=(9x2-16)
-(6x2+5x -6)
=3x2-5x- 10.
解:原式=(a)2-(3b)2
(2)(3+2a)(-3+2a);
(4)(3x+4)(3x-4)-(2x+3)(3x-2).
(3)(-2x2-y)(-2x2+y);
5.利用平方差公式计算:
课堂小结
平方差公式
内容
注意事项
两个数的和与这两个数的差的积,等于这两个数的平方差
紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式
符号表示:(a+b)(a-b)=a2-b2
第八章 整式的乘法
8.5 第1课时 平方差公式
知识回顾
多项式与多项式是如何相乘的?
(x + 3)( x+5)
=x2
+5x
+3x
+15
=x2
+8x
+15.
(a+b)(m+n)
=am
+an
+bm
+bn
情景导入
“灰太狼的阴谋”?
灰太狼开起了租地公司,他把一块边长
为a米的正方形土地租给慢羊羊种植.有一年他对慢羊羊说:“我把这块地的一边增加5米,另一边减少5米,再继续租给你, 你也没吃亏,你看如何 ”慢羊羊一听觉得没有吃亏,就答应了.回到羊村,就把这件事对喜羊羊他们讲了,喜羊羊一听,就说道:“村长,您吃亏了!” 慢羊羊村长很吃惊…
同学们,你认为慢羊羊吃亏了吗?
5米
5米
a米
(a-5)米
(a+5)米
面积相等吗?
原来
现在
a2
(a+5)(a-5)
获取新知
①(x + 1)( x-1);
②(m + 2)( m-2);
③(2m+ 1)(2m-1);
④(5y + z)(5y-z).
问题1:计算下列多项式的积,你能发现什么规律?
x2 - 12
m2-22
(2m)2 - 12
(5y)2 - z2
想一想:这些计算结果有什么共同特点?
知识点
平方差的特征
1
两数和
两数差
两数平方差
两个数的和与这两个数的差的积,等于这两个数的平方差.
平方差公式
注:这里的a,b可以是单项式,也可以是多项式等.
左边=
=右边
代数验证
(多项式乘以多项式的法则)
(合并同类项法则)
问题2
如图,在一个边长为a的正方形中,剪去一个边长为b的小正方形,再将余下的部分剪拼成一个长方形.
(1)两个图形(着色部分)的面积之间有什么关系?
(2)请你结合图形对平方差公式(a+b)(a-b)=a2-b2进行解释.
b
a
图1
相等
图1:a2-b2
图2:长:(a+b),宽:(a-b)
面积:(a+b)(a-b)
b
a
图2
b
a2-b2=(a+b)(a-b)
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
a-b
a-b
几何验证
面积法
算式 与平方差公式中a对应的项 与平方差公式中b对应的项 写成“a2-b2”的形式 计算结果
(m+2)(m-2)
(2m+3)(2m-3)
(x+2y)(-x+2y)
(1+3y)(1-3y)
问题3
按要求填写下面的表格:
m
2
m2-22
m2-4
2m
3
(2m)2-32
4m2-9
2y
x
(2y)2-x2
4y2-x2
1
3y
12-(3y)2
1-9y2
知识点
平方差公式的运用
2
例题讲解
例1 计算:
a
b
解:
利用平方差公式计算,必须找到相同的项和互为相反数的项
a
b
a
b
例2 用平方差公式计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .
解: (1) 102×98
(2) (y+2)(y-2)- (y-1)(y+5)
= 1002-22
=10000 – 4
=(100+2)(100-2)
=9996
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.
1.下列各式中,能用平方差公式运算的是( )
A.(-a+b)(-a-b) B.(a-b)(b-a)
C.(2a-3b)(3a+2b) D .(-2y-x)(x+2y)
A
随堂演练
2.计算(2x+3)(2x-3)的值是( )
A.4x2-9 B.4x2-3
C.2x2-9 D.2x2-3
A
3.计算:
(1)(x+1)(x-____)=x2-1;
(2)(x+3y)______=9y2-x2.
(3y-x)
1
4.下面各式的计算对不对?如果不对,应当怎样改正?
(1)(x+2)(x-2)=x2-2
(2)(-3a-2)(3a-2)=9a2-4
不对
改正:
(1)(x+2)(x-2)=x2-4
不对
改正方法1:
(-3a-2)(3a-2)=-[(3a+2)(3a-2)]=-(9a2-4)=-9a2+4.
改正方法2:
(-3a-2)(3a-2)=(-2-3a)(-2+3a)=(-2)2-(3a)2=4-9a2
(1)(a+3b)(a- 3b);
=4a2-9;
=4x4-y2;
原式=(2a+3)(2a-3)
=a2-9b2 ;
=(2a)2-32
原式=(-2x2 )2-y2
原式=(9x2-16)
-(6x2+5x -6)
=3x2-5x- 10.
解:原式=(a)2-(3b)2
(2)(3+2a)(-3+2a);
(4)(3x+4)(3x-4)-(2x+3)(3x-2).
(3)(-2x2-y)(-2x2+y);
5.利用平方差公式计算:
课堂小结
平方差公式
内容
注意事项
两个数的和与这两个数的差的积,等于这两个数的平方差
紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式
符号表示:(a+b)(a-b)=a2-b2
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
