冀教版数学七年级下册同步课件:9.1三角形的边(共25张PPT)
文档属性
| 名称 | 冀教版数学七年级下册同步课件:9.1三角形的边(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 390.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 09:28:37 | ||
图片预览






文档简介
(共25张PPT)
第九章 三角形
9.1 三角形的边
情景导入
生活中随处可见三角形
1.观察下图中图形的构成,试着发现它们的规律.
2.下图是用三根细木棒组成的图形,你认为下列图形是三角形吗?木棒怎样才能拼成三角形呢?
(4)
(1)
(3)
(2)
(5)
知识点
三角形的有关概念
1
新知探究
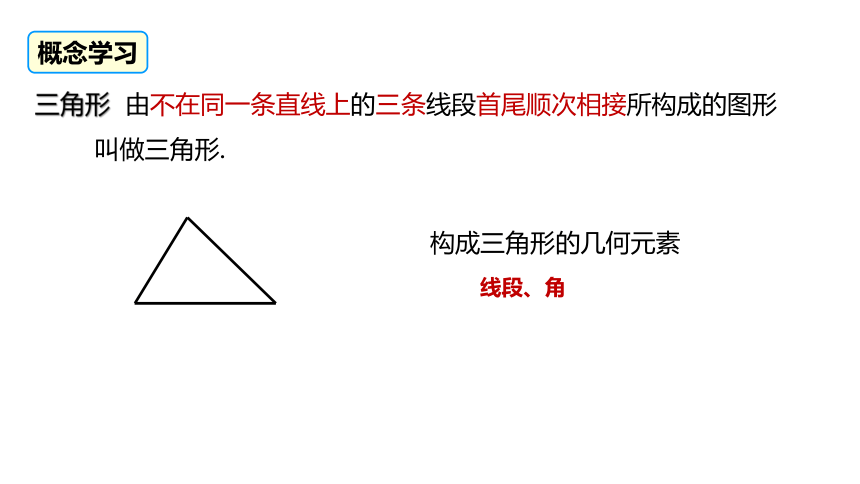
三角形 由不在同一条直线上的三条线段首尾顺次相接所构成的图形
叫做三角形.
构成三角形的几何元素
线段、角
概念学习
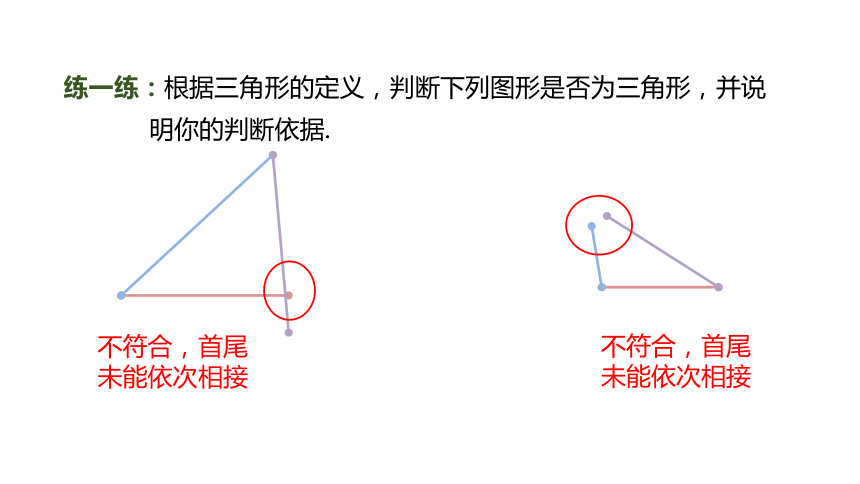
练一练:根据三角形的定义,判断下列图形是否为三角形,并说明你的判断依据.
不符合,首尾未能依次相接
不符合,首尾未能依次相接
如图,三角形有
三条边,三个角,三个顶点.
A
B
C
顶点:点A,点B,点C
读作:三角形ABC
边:AB,BC,AC
或a,b,c
内角:∠A,∠B,∠C
a
b
c
三角形要素及三角形表示方法
以点A、B、C为顶点的三角形记为 ,
符号语言
B
C
A
点A,点B,点C
∠A,∠B,∠C
边AB,BC,AC
边MP,PQ,MQ
∠M,∠P,∠Q
点M,点P,点Q
∠A,∠B,∠C
点A,点B,点C
P
Q
M
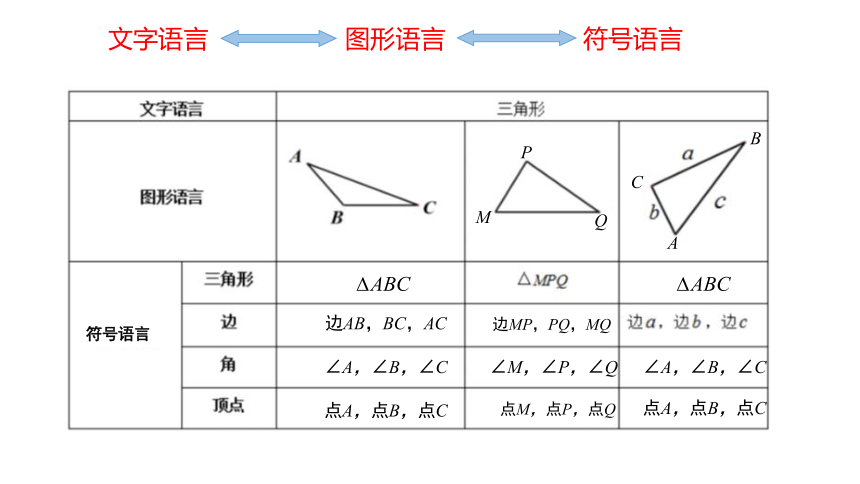
文字语言
图形语言
符号语言
练一练
如图所示,三角形ABE可记作 ,
它的三个顶点是 , , ,
三条边是 , , ,
三个内角分别是 .
△ABE
点A
点B
点E
AE
AB
BE
∠ABE, ∠BAE, ∠AEB
每组课前准备四根木条,分别长为2 cm,3 cm,4 cm,5 cm,现在从其中任取三根相接来摆三角形,试试能否成功?做好实验记录,并分类汇总实验.
知识点
三角形的三边关系
2
一起探究
实验数据记录在下表:
三根木棒的长度cm 能否构成三角形 任意两根木棒长度的和与第三根的关系 (用数字表示)
2,3,5
2,3,4
2,4,5
3,4,5
否
能
能
能
2+3=5,2+5>3 , 3+5>2
2+3>4,2+4>3 , 3+4>2
2+4>5,2+5>4 , 4+5>2
3+4>5,3+5>4 , 4+5>3
大家谈谈:1.是不是任意三根木棒都能拼成三角形呢?谈谈哪些试验是失败的?找出失败的原因,并总结什么样的三条线段能拼成三角形?
2. 由以上探索,你能归纳出三角形任意两边之和与第三边的关系吗?
猜想:三角形任意两边之和大于第三边
如何说明呢?
B
A
C
已知△ABC.
说明:AB+AC>BC,
AC+BC>AB,AB+BC>AC
说理过程:∵AB是线段,
∴AC+BC>AB,(两点之间,线段最短)
同理可得:AB+BC>AC,AB+AC>BC.
归纳:三角形任意两边之和大于第三边.
例1 长度为6cm,4cm,3cm三条线段能否组成三角形?
解:∵6+4>3
6+3>4
4+3>6
∴能组成三角形
解: ∵最长线段是6cm
4+3>6
∴能组成三角形
例题讲解
方法点拨:判断三条线段能否组成三角形的方法:
①找出最长线段;
②比较较短两条线段之和与最长线段的大小;
③若较短两条线段之和大于最长线段,则能组成三角形,否则不能组成三角形.
练一练 1.下列长度的三条线段能否组成三角形?
(1) 3,8,4
(2) 2,5,6
(3) 5,6,10
(4) 3,5,8
不能
能
能
不能
大家谈谈
已知一个三角形的最小边为2 cm,另两边分别为6 cm和a cm , a的取值范围是什么?
大家谈谈:观察下图中的三角形,试着比较它们之间的不同之处.
提示:可根据三角形三边的长度关系进行比较
不等边三角形
(三条边长度均不相等)
等腰三角形
(两条边长度相等)
等边三角形
(三条边长度相等)
顶角
底角
腰
底边
知识点
三角形的分类
3
三条边各不相等的三角形叫做不等边三角形.
有两条边相等的三角形叫做等腰三角形. 相等的两边叫做腰,另一边叫做底边.
三条边都相等的三角形叫做等边三角形 .
等腰三角形与等边三角形的关系:
等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形.
概念学习
三角形的分类
两边相等的等腰三角形
三边相等的等腰三角形
等边三角形
三角形
等腰三角形
不等边三角形
按边分
三角形
不等边三角形
等腰三角形
等边三角形
1.三角形是指( )
A.由三条线段所组成的封闭图形
B.由不在同一直线上的三条直线首尾顺次相接组成的图形
C.由不在同一直线上的三条线段首尾顺次相接组成的图形
D.由三条线段首尾顺次相接组成的图形
C
随堂演练
A
2.以下列各组线段的长为边,能组成三角形的是( )
A.2 cm,3 cm,4 cm
B.2 cm,3 cm,5 cm
C.2 cm,5 cm,10 cm
D.8 cm,4 cm,4 cm
3.已知等边三角形其中一边的长为4cm,则这个三角形的周长为( )cm.
A.8 B.12 C.16 D.不能确定
B
4.图中共有几个三角形?用符号表示这些三角形.
A
D
C
B
O
图中共有5个三角形:
△ABO、△ABC、△ABD、△ADO、△BOC.
课堂小结
三角形
概念:由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形.
分类
不等边三角形
等腰三角形(包括等边三角形)
三边关系
任意两边之和大于第三边
第九章 三角形
9.1 三角形的边
情景导入
生活中随处可见三角形
1.观察下图中图形的构成,试着发现它们的规律.
2.下图是用三根细木棒组成的图形,你认为下列图形是三角形吗?木棒怎样才能拼成三角形呢?
(4)
(1)
(3)
(2)
(5)
知识点
三角形的有关概念
1
新知探究
三角形 由不在同一条直线上的三条线段首尾顺次相接所构成的图形
叫做三角形.
构成三角形的几何元素
线段、角
概念学习
练一练:根据三角形的定义,判断下列图形是否为三角形,并说明你的判断依据.
不符合,首尾未能依次相接
不符合,首尾未能依次相接
如图,三角形有
三条边,三个角,三个顶点.
A
B
C
顶点:点A,点B,点C
读作:三角形ABC
边:AB,BC,AC
或a,b,c
内角:∠A,∠B,∠C
a
b
c
三角形要素及三角形表示方法
以点A、B、C为顶点的三角形记为 ,
符号语言
B
C
A
点A,点B,点C
∠A,∠B,∠C
边AB,BC,AC
边MP,PQ,MQ
∠M,∠P,∠Q
点M,点P,点Q
∠A,∠B,∠C
点A,点B,点C
P
Q
M
文字语言
图形语言
符号语言
练一练
如图所示,三角形ABE可记作 ,
它的三个顶点是 , , ,
三条边是 , , ,
三个内角分别是 .
△ABE
点A
点B
点E
AE
AB
BE
∠ABE, ∠BAE, ∠AEB
每组课前准备四根木条,分别长为2 cm,3 cm,4 cm,5 cm,现在从其中任取三根相接来摆三角形,试试能否成功?做好实验记录,并分类汇总实验.
知识点
三角形的三边关系
2
一起探究
实验数据记录在下表:
三根木棒的长度cm 能否构成三角形 任意两根木棒长度的和与第三根的关系 (用数字表示)
2,3,5
2,3,4
2,4,5
3,4,5
否
能
能
能
2+3=5,2+5>3 , 3+5>2
2+3>4,2+4>3 , 3+4>2
2+4>5,2+5>4 , 4+5>2
3+4>5,3+5>4 , 4+5>3
大家谈谈:1.是不是任意三根木棒都能拼成三角形呢?谈谈哪些试验是失败的?找出失败的原因,并总结什么样的三条线段能拼成三角形?
2. 由以上探索,你能归纳出三角形任意两边之和与第三边的关系吗?
猜想:三角形任意两边之和大于第三边
如何说明呢?
B
A
C
已知△ABC.
说明:AB+AC>BC,
AC+BC>AB,AB+BC>AC
说理过程:∵AB是线段,
∴AC+BC>AB,(两点之间,线段最短)
同理可得:AB+BC>AC,AB+AC>BC.
归纳:三角形任意两边之和大于第三边.
例1 长度为6cm,4cm,3cm三条线段能否组成三角形?
解:∵6+4>3
6+3>4
4+3>6
∴能组成三角形
解: ∵最长线段是6cm
4+3>6
∴能组成三角形
例题讲解
方法点拨:判断三条线段能否组成三角形的方法:
①找出最长线段;
②比较较短两条线段之和与最长线段的大小;
③若较短两条线段之和大于最长线段,则能组成三角形,否则不能组成三角形.
练一练 1.下列长度的三条线段能否组成三角形?
(1) 3,8,4
(2) 2,5,6
(3) 5,6,10
(4) 3,5,8
不能
能
能
不能
大家谈谈
已知一个三角形的最小边为2 cm,另两边分别为6 cm和a cm , a的取值范围是什么?
大家谈谈:观察下图中的三角形,试着比较它们之间的不同之处.
提示:可根据三角形三边的长度关系进行比较
不等边三角形
(三条边长度均不相等)
等腰三角形
(两条边长度相等)
等边三角形
(三条边长度相等)
顶角
底角
腰
底边
知识点
三角形的分类
3
三条边各不相等的三角形叫做不等边三角形.
有两条边相等的三角形叫做等腰三角形. 相等的两边叫做腰,另一边叫做底边.
三条边都相等的三角形叫做等边三角形 .
等腰三角形与等边三角形的关系:
等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形.
概念学习
三角形的分类
两边相等的等腰三角形
三边相等的等腰三角形
等边三角形
三角形
等腰三角形
不等边三角形
按边分
三角形
不等边三角形
等腰三角形
等边三角形
1.三角形是指( )
A.由三条线段所组成的封闭图形
B.由不在同一直线上的三条直线首尾顺次相接组成的图形
C.由不在同一直线上的三条线段首尾顺次相接组成的图形
D.由三条线段首尾顺次相接组成的图形
C
随堂演练
A
2.以下列各组线段的长为边,能组成三角形的是( )
A.2 cm,3 cm,4 cm
B.2 cm,3 cm,5 cm
C.2 cm,5 cm,10 cm
D.8 cm,4 cm,4 cm
3.已知等边三角形其中一边的长为4cm,则这个三角形的周长为( )cm.
A.8 B.12 C.16 D.不能确定
B
4.图中共有几个三角形?用符号表示这些三角形.
A
D
C
B
O
图中共有5个三角形:
△ABO、△ABC、△ABD、△ADO、△BOC.
课堂小结
三角形
概念:由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形.
分类
不等边三角形
等腰三角形(包括等边三角形)
三边关系
任意两边之和大于第三边
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
