冀教版数学七年级下册同步课件:10.3 第1课时 一元一次不等式的有关概念(共22张PPT)
文档属性
| 名称 | 冀教版数学七年级下册同步课件:10.3 第1课时 一元一次不等式的有关概念(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 791.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
第十章 一元一次不等式和一元一次不等式组
10.3 第1课时 一元一次不等式的有关概念
不等式的基本性质1:不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向不变。
不等式的基本性质2:不等式的两边都乘(或除以)同一个正数,不等号的方向不变。
不等式的基本性质3:不等式的两边都乘(或除以)同一个负数,不等号的方向改变。
知识回顾
不等式的基本性质有哪些?
80x
天平左边质量为60(x+1),天平右边质量为80x,你能判断哪边的质量大,并列出不等式吗?
60(x+1)
80x>60(x+1)
情景导入
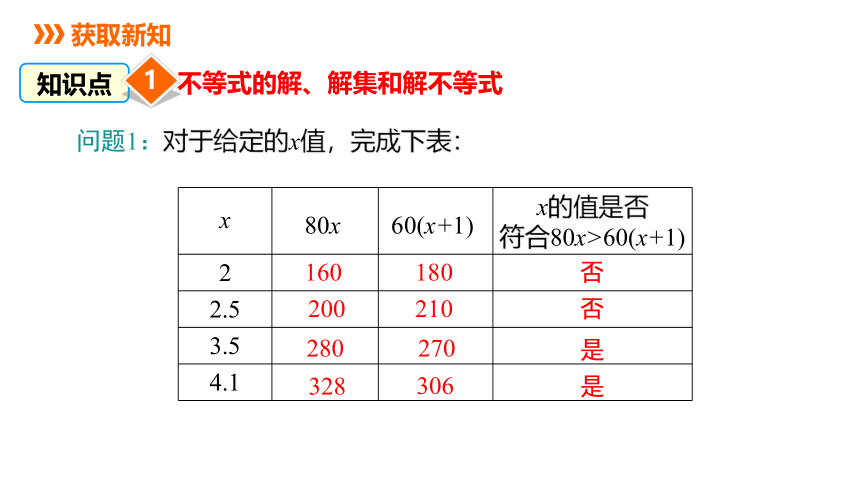
问题1:对于给定的x值,完成下表:
x的值是否
符合80x>60(x+1)
2
2.5
3.5
4.1
是
x
210
否
否
306
是
160
200
328
80x
180
60(x+1)
280
270
获取新知
知识点
不等式的解、解集和解不等式
1
概念学习
对于含有未知数的不等式,能使不等式成立的未知数的值,叫做不等式的解.
不等式的解
问题2:上述数值3.5,4.1都满足不等式80x>60(x+1),那么我们可以把这些数值叫做什么?
问题3:数4,5,5.5是不等式80x>60(x+1)的解吗?你认为不等式80x>60(x+1)的解有多少个?
一个含未知数的不等式的所有解组成这个不等式的解集.
无数个
求不等式解集的过程,叫做解不等式.
概念学习
是
不等式的解 不等式的解集
区别 定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解是解集中的一员
解集包括了某个解
不等式的解与不等式的解集的区别与联系
练一练
下列不等式中,不含有x=-1这个解的是 ( )
A. 2x+1≤-3 B. 2x-1≥-3
C. -2x+1≥3 D. -2x-1≤3
A
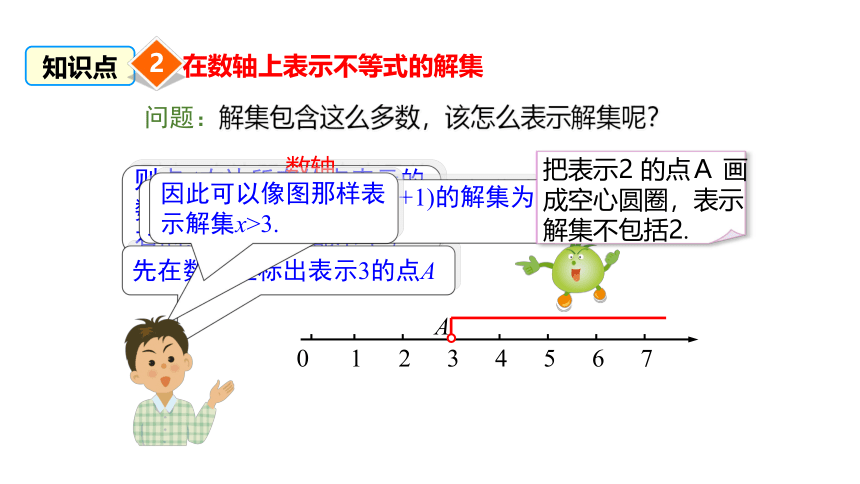
则点A右边所有的点表示的数都大于3,而点A左边所有的点表示的数都小于3
先在数轴上标出表示3的点A
例如,不等式80x>60(x+1)的解集为x>3.
问题:解集包含这么多数,该怎么表示解集呢?
数轴
因此可以像图那样表示解集x>3.
1
2
3
4
5
6
7
0
A
把表示2 的点A 画成空心圆圈,表示解集不包括2.
知识点
在数轴上表示不等式的解集
2
则点B右边所有的点表示的数都大于-1,而点B左边所有的点表示的数都小于-1
-5
-4
-3
-2
-1
0
1
-6
B
把表示-1 的点B画成实心圆点,表示解集包括-1.
同理,不等式-2x≥2的解集为x≤-1.
先在数轴上标出表示-1的点B
因此可以像图那样表示解集x≤-1.
归纳总结
在数轴上表示不等式的解集时,要确定边界和方向.
(1) 边界:有等号的是实心圆点,无等号的是空心圆圈.
(2) 方向:大于向右,小于向左.
1.把不等式x>2的解集表示在数轴上,正确的是( )
【解析】根据“大于向右画,无等画圆圈”可知选项B符合.
练一练
2.如图,数轴所表示的不等式的解集是 .
0
4
B
x≤4
问题:观察下列不等式:80x>60(x+1),x>3,m+10≤
m,2x<x+2.
这些不等式中都含有几个未知数?
那么这些未知数的次数又是几?
归纳总结
我们把含有一个未知数,并且未知数的次数都是1的不等式叫做一元一次不等式.
一个未知数
一次
知识点
一元一次不等式
3
例1 已知 是关于x的一元一次不等式,
则a的值是________.
解析:由 是关于x的一元一次不等式得2a-1=1,计算即可求出a=1.
1
例题讲解
判断下列不等式是否为一元一次不等式.
(1)3x-2>7 (6)
(2)x2≤6 (7)2(1-y)+y<2y+3
(3)x+y≤3y+2 (8)x2-2x+1=0
(4)
(5)-2<3
是
否
否
否
否
否
是
否
练一练
例2 解不等式 x+1<5,并把解集在数轴上表示出来.
解:不等式两边都减去1,得
x<5-1,
即 x<4.
两边都乘以2(或除以 ),得
x<8.
3
4
5
6
7
8
9
○
2
1
0
-1
1. 下列说法正确的是 ( )
A.x=4是x+3<5的解 B.x=1是不等式x-1>0的解
C.x=3是x+3≥6的唯一解 D.x<5是2x<10的解集
D
2. 下列不等式中,是一元一次不等式的有( )
①3x﹣7>0;②2x+y>3;③2x2﹣x>﹣1;
④ +1<7.
A
A.1个 B.2个 C.3个 D.4个
随堂演练
3.将下列不等式的解集分别表示在数轴上:
(1) x>4; (2) x<- 1 ;
(3)x≥-2; (4) x≤6.
解:(1)如图所示.
(2)如图所示.
(3)如图所示.
(4)如图所示.
4.请写出下列各数轴上所表示的关于x的不等式的解集.
解:(1)x<-1;(2)x>3
(1) 2-2x > 4;
解:两边都减去2,得
-2x>4-2,即 -2x>2,
两边同时除以-2,得
x< -1.
在数轴上表示如图:
0
-1
5. 解下列不等式,并把解集在数轴上表示出来.
(2)
解:两边同时除以-7,得
x≥ -7.
在数轴上表示如图:
-7
0
一元一次不等式的有关概念
不等式的解与解集
在数轴上
表示不等式
能使含未知数的不等式成立的未知数的值叫___________.
一个含未知数的不等式的所有解组成这个不等式的_____.
求解不等式解集的过程,叫做____________.
方向:大于向__,小于向__
边界:________包含边界,
________不包含边界.
一元一次
不等式
含有 未知数.
未知数的次数为_____.
不等式的解
解集
解不等式
右
左
实心点
空心圆圈
一个
一次
课堂小结
第十章 一元一次不等式和一元一次不等式组
10.3 第1课时 一元一次不等式的有关概念
不等式的基本性质1:不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向不变。
不等式的基本性质2:不等式的两边都乘(或除以)同一个正数,不等号的方向不变。
不等式的基本性质3:不等式的两边都乘(或除以)同一个负数,不等号的方向改变。
知识回顾
不等式的基本性质有哪些?
80x
天平左边质量为60(x+1),天平右边质量为80x,你能判断哪边的质量大,并列出不等式吗?
60(x+1)
80x>60(x+1)
情景导入
问题1:对于给定的x值,完成下表:
x的值是否
符合80x>60(x+1)
2
2.5
3.5
4.1
是
x
210
否
否
306
是
160
200
328
80x
180
60(x+1)
280
270
获取新知
知识点
不等式的解、解集和解不等式
1
概念学习
对于含有未知数的不等式,能使不等式成立的未知数的值,叫做不等式的解.
不等式的解
问题2:上述数值3.5,4.1都满足不等式80x>60(x+1),那么我们可以把这些数值叫做什么?
问题3:数4,5,5.5是不等式80x>60(x+1)的解吗?你认为不等式80x>60(x+1)的解有多少个?
一个含未知数的不等式的所有解组成这个不等式的解集.
无数个
求不等式解集的过程,叫做解不等式.
概念学习
是
不等式的解 不等式的解集
区别 定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解是解集中的一员
解集包括了某个解
不等式的解与不等式的解集的区别与联系
练一练
下列不等式中,不含有x=-1这个解的是 ( )
A. 2x+1≤-3 B. 2x-1≥-3
C. -2x+1≥3 D. -2x-1≤3
A
则点A右边所有的点表示的数都大于3,而点A左边所有的点表示的数都小于3
先在数轴上标出表示3的点A
例如,不等式80x>60(x+1)的解集为x>3.
问题:解集包含这么多数,该怎么表示解集呢?
数轴
因此可以像图那样表示解集x>3.
1
2
3
4
5
6
7
0
A
把表示2 的点A 画成空心圆圈,表示解集不包括2.
知识点
在数轴上表示不等式的解集
2
则点B右边所有的点表示的数都大于-1,而点B左边所有的点表示的数都小于-1
-5
-4
-3
-2
-1
0
1
-6
B
把表示-1 的点B画成实心圆点,表示解集包括-1.
同理,不等式-2x≥2的解集为x≤-1.
先在数轴上标出表示-1的点B
因此可以像图那样表示解集x≤-1.
归纳总结
在数轴上表示不等式的解集时,要确定边界和方向.
(1) 边界:有等号的是实心圆点,无等号的是空心圆圈.
(2) 方向:大于向右,小于向左.
1.把不等式x>2的解集表示在数轴上,正确的是( )
【解析】根据“大于向右画,无等画圆圈”可知选项B符合.
练一练
2.如图,数轴所表示的不等式的解集是 .
0
4
B
x≤4
问题:观察下列不等式:80x>60(x+1),x>3,m+10≤
m,2x<x+2.
这些不等式中都含有几个未知数?
那么这些未知数的次数又是几?
归纳总结
我们把含有一个未知数,并且未知数的次数都是1的不等式叫做一元一次不等式.
一个未知数
一次
知识点
一元一次不等式
3
例1 已知 是关于x的一元一次不等式,
则a的值是________.
解析:由 是关于x的一元一次不等式得2a-1=1,计算即可求出a=1.
1
例题讲解
判断下列不等式是否为一元一次不等式.
(1)3x-2>7 (6)
(2)x2≤6 (7)2(1-y)+y<2y+3
(3)x+y≤3y+2 (8)x2-2x+1=0
(4)
(5)-2<3
是
否
否
否
否
否
是
否
练一练
例2 解不等式 x+1<5,并把解集在数轴上表示出来.
解:不等式两边都减去1,得
x<5-1,
即 x<4.
两边都乘以2(或除以 ),得
x<8.
3
4
5
6
7
8
9
○
2
1
0
-1
1. 下列说法正确的是 ( )
A.x=4是x+3<5的解 B.x=1是不等式x-1>0的解
C.x=3是x+3≥6的唯一解 D.x<5是2x<10的解集
D
2. 下列不等式中,是一元一次不等式的有( )
①3x﹣7>0;②2x+y>3;③2x2﹣x>﹣1;
④ +1<7.
A
A.1个 B.2个 C.3个 D.4个
随堂演练
3.将下列不等式的解集分别表示在数轴上:
(1) x>4; (2) x<- 1 ;
(3)x≥-2; (4) x≤6.
解:(1)如图所示.
(2)如图所示.
(3)如图所示.
(4)如图所示.
4.请写出下列各数轴上所表示的关于x的不等式的解集.
解:(1)x<-1;(2)x>3
(1) 2-2x > 4;
解:两边都减去2,得
-2x>4-2,即 -2x>2,
两边同时除以-2,得
x< -1.
在数轴上表示如图:
0
-1
5. 解下列不等式,并把解集在数轴上表示出来.
(2)
解:两边同时除以-7,得
x≥ -7.
在数轴上表示如图:
-7
0
一元一次不等式的有关概念
不等式的解与解集
在数轴上
表示不等式
能使含未知数的不等式成立的未知数的值叫___________.
一个含未知数的不等式的所有解组成这个不等式的_____.
求解不等式解集的过程,叫做____________.
方向:大于向__,小于向__
边界:________包含边界,
________不包含边界.
一元一次
不等式
含有 未知数.
未知数的次数为_____.
不等式的解
解集
解不等式
右
左
实心点
空心圆圈
一个
一次
课堂小结
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
