物理人教版(2019)必修第二册8.1功与功率(共46张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册8.1功与功率(共46张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-27 22:19:30 | ||
图片预览








文档简介
(共46张PPT)
8.1 功和功率
第八章 机械能守恒定律
叉车竖直提升重物时,力的方向与物体的运动方向一致,则力对物体做功为多少?
W=FL
F
L
F
功
1
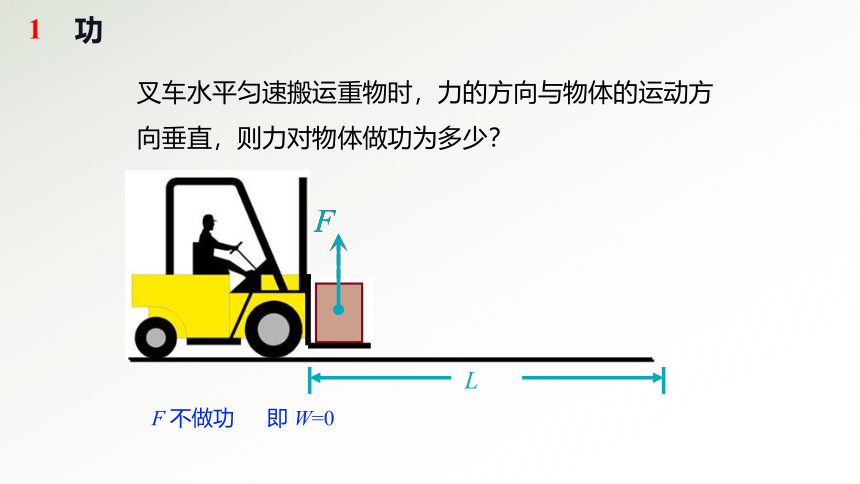
叉车水平匀速搬运重物时,力的方向与物体的运动方向垂直,则力对物体做功为多少?
F 不做功 即 W=0
L
F
F
功
1
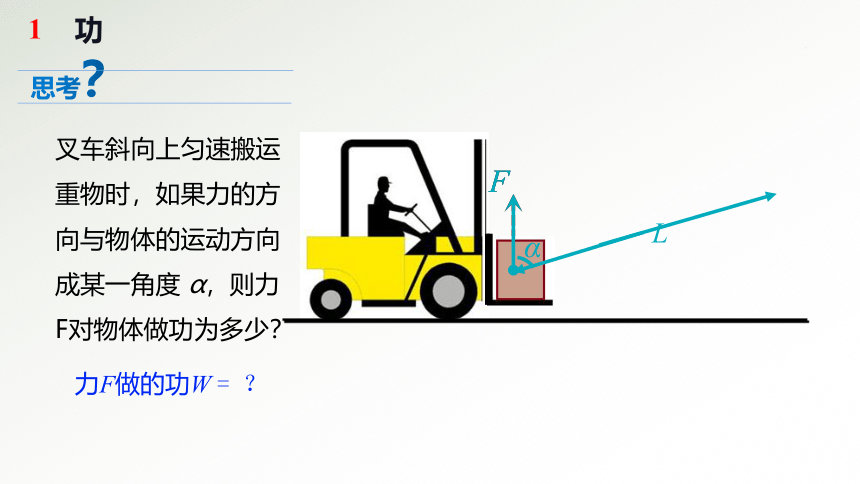
力F做的功W = ?
叉车斜向上匀速搬运重物时,如果力的方向与物体的运动方向成某一角度 α,则力F对物体做功为多少?
F
F
L
α
功
1
思考?
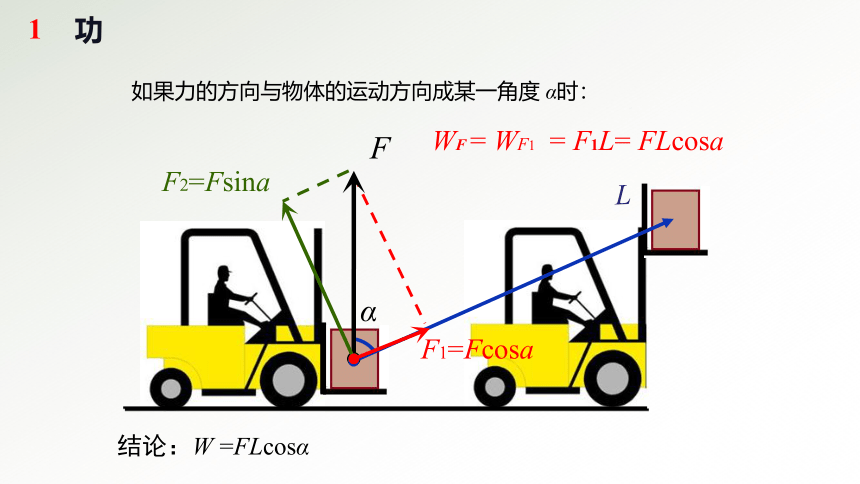
如果力的方向与物体的运动方向成某一角度 α时:
F
L
α
L1=Lcos α
L2=Lsinɑ
WF = FL1= FLcos α
还有别的方法求力F所做的功吗?
结论:W =FLcosα
功
1
思考?
如果力的方向与物体的运动方向成某一角度 α时:
F
α
结论:W =FLcosα
L
F2=Fsinɑ
F1=Fcosɑ
WF = WF1 = F1L= FLcosɑ
功
1
W=F L cosα
力F对物体做的功
力的大小
位移的大小
力与位移的方向的夹角
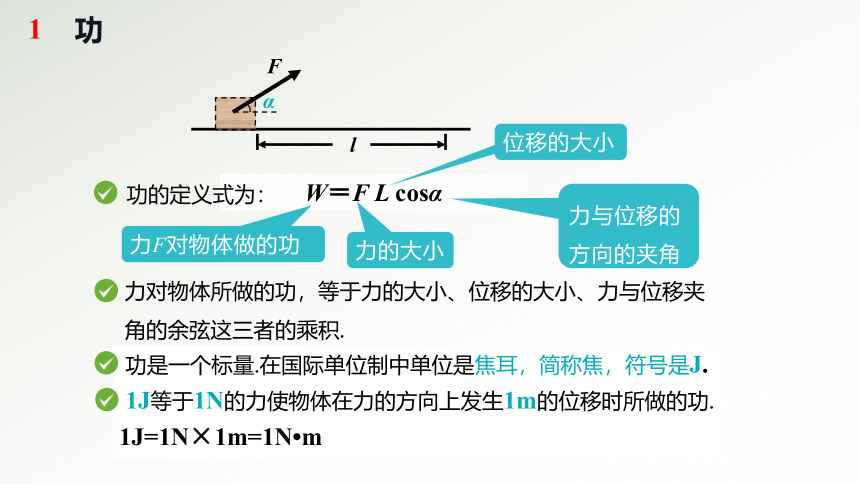
功的定义式为:
力对物体所做的功,等于力的大小、位移的大小、力与位移夹角的余弦这三者的乘积.
功是一个标量.在国际单位制中单位是焦耳,简称焦,符号是J.
1J等于1N的力使物体在力的方向上发生1m的位移时所做的功.
1J=1N×1m=1N m
l
F
α
功
1
辨认力的方向与位移方向的夹角
450
F
L
甲
答案:450
450
F
L
乙
答案:1350
450
F
L
丙
答案:450
450
F
L
丁
答案: 1350
方法:将力、位移矢量的箭尾移到同一个作用点上。
功
1
思考?
例1.一个质量为150kg的物体,受到与水平方向成α=37°角的斜向右上方的拉力F1=500N的作用,在水平地面上移动的距离为L=5m,物体与地面间的滑动摩擦力F2=100N,求拉力F1和滑动摩擦力F2做的功?
F1
37°
F2
v
解析:拉力F1对物体所做的功为:W1=F1Lcosα1= F1Lcos37°= 2000J
摩擦力F2对物体所做的功为:W2=F2Lcosα2= F2Lcos180°= –500J
矢量的正、负表示的是方向.功是标量,它的正、负表示什么意思呢?
功
1
思考?
某力对物体做负功,往往说成“物体克服某力做功”(取绝对值),两种说法的意义是等同的。
时,cosα>0,
W>0 力对物体做正功,
促进物体的运动.
时,cosα<0,
W<0力对物体做负功,
阻碍物体的运动.
时,cosα=0,
W =0 力对物体不做功.
功
1
例2.一个质量m=150kg的雪撬,受到与水平方向成θ=37 °角斜向上方的拉力F=500N,在水平地面上移动的距离L=5m.物体与地面间的滑动摩擦力F阻=100N.求力对物体所做的总功.
v
F
θ
FN
G
F阻
W拉=FLcosθ=FLcos37°
阻力做的功
W阻=F阻L cos180°=- F阻L
代入数据,得 W合=1500 J
W合=W拉+W阻=FL cos37°-F阻L
力做的总功
拉力F做的功
解:重力和支持力与运动方向垂直,对物体不做功
思考分析:(1)物体受力情况如何?(2)各个力做功如何?
功
1
例2.一个质量m=150kg的雪撬,受到与水平方向成θ=37 °角斜向上方的拉力F=500N,在水平地面上移动的距离L=5m.物体与地面间的滑动摩擦力F阻=100N.求力对物体所做的总功.
功
1
思考分析:
(1)物体受力情况如何?
(2)物体所受合力是多少?
(3)合力做功多少?
还有其他方法吗?
例2.一个质量m=150kg的雪撬,受到与水平方向成θ=37 °角斜向上方的拉力F=500N,在水平地面上移动的距离L=5m.物体与地面间的滑动摩擦力F阻=100N.求力对物体所做的总功.
功
1
v
F
θ
FN
G
F阻
F1=Fcosθ
代入数据,得 W合=1500 J
W合=F合 L cos0°= (Fcos θ - F阻)L
力对雪橇做的总功
F1
F2
F2=Fsinθ
F合=F1 -F阻= Fcosθ- F阻
解:
总功的求法
W总=W1+W2+W3+
1、功是标量
故合力的功(即总功)就等于各分力做功的代数和:
W总=F合 Lcos α
2、力是矢量
故可以先求合力,再求合力做的功:
功
1
例3 (多选)质量为m的物体,静止在倾角为θ的斜面上,斜面沿水平方向向右匀速移动了距离l,如图7所示.物体始终相对斜面静止,则下列说法正确的是
A.重力对物体做正功
B.合力对物体做功为零
C.摩擦力对物体做负功
D.支持力对物体做正功
√
图7
√
√
功
1
一台耕地机一天能耕地约 20亩田地
一头牛一天能耕地 5 亩 田地
谁做功更快?
定义:功与完成这些功所用时间的比值,叫作功率。
公式:
1 W=1 J/s
物理意义:反映物体做功的快慢。
单位:瓦特(国际单位制),简称瓦,符号是 W
功率是标量
功率
2
长时间运动时人的功率为数10W,优秀运动员可达1kW
长时间运动马的功率为数百瓦
鲸游动时功率可达350kW
小汽车的功率为数十千瓦至两百千瓦
高速列车的功率可达数万kW
万吨豪华游轮的功率可达1万kW以上
功率
2
W=Fl
P=Fv
P=
t
Fl
v=
t
l
P =
t
W
若力与位移的方向在同一直线:
关于功率的另一种表达形式
若力与位移的方向成某一角度 α 时 :
W=Flcosα
P=Fvcosα
P=
t
Flcosα
v=
t
l
P=
t
W
功率
2
v
F
α
v1
v2
F
α
v
F2
F1
P=vFcos α
P=Fvcos α
对公式:P=Fvcos α的理解
功率
2
平均功率:描述在一段时间内做功的平均快慢
瞬时功率:表示在某一时刻做功的快慢
讨论:
分别可以用哪个公式求平均功率和瞬时功率?
平均功率和瞬时功率
(1)求平均功率
(v是平均速度)
(2)求瞬时功率
(v是瞬时速度)
比较常用
(对应一段时间或一个过程)
(对应一个时刻或一个位置)
功率
2
例1 关于功率,下列说法正确的是
√
功率
2
例2 某人用同一水平力F先后两次拉同一物体,第一次使此物体从静止开始在光滑水平面上前进l距离,第二次使此物体从静止开始在粗糙水平面上前进l距离.若先后两次拉力做的功分别为W1和W2,拉力做功的平均功率分别为P1和P2,则
A.W1=W2,P1=P2 B.W1=W2,P1>P2
C.W1>W2,P1>P2 D.W1>W2,P1=P2
√
功率
2
例3 如图1所示,质量为m=2 kg的木块在倾角θ=37°的足够长的固定斜面上由静止开始下滑,木块与斜面间的动摩擦因数为μ=0.5,已知:sin 37°=0.6,cos 37°=0.8,g取10 m/s2,求:
(1)前2 s内重力做的功;
图1
功率
2
解析 木块下滑过程中,由牛顿第二定律得:
mgsin θ-μmgcos θ=ma
联立解得:x=4 m,a=2 m/s2
所以重力在前2 s内做的功为W=mgsin θ·x=2×10×0.6×4 J=48 J;
例3 如图1所示,质量为m=2 kg的木块在倾角θ=37°的足够长的固定斜面上由静止开始下滑,木块与斜面间的动摩擦因数为μ=0.5,已知:sin 37°=0.6,cos 37°=0.8,g取10 m/s2,求:
(2)前2 s内重力的平均功率;
图1
功率
2
例3 如图1所示,质量为m=2 kg的木块在倾角θ=37°的足够长的固定斜面上由静止开始下滑,木块与斜面间的动摩擦因数为μ=0.5,已知:sin 37°=0.6,cos 37°=0.8,g取10 m/s2,求:
图1
功率
2
(3)2 s末重力的瞬时功率.
解析 木块在2 s末的速度大小为
v=at=2×2 m/s=4 m/s
2 s末重力的瞬时功率为
P=mgsin θ·v=2×10×0.6×4 W=48 W.
想一想,物体在水平面上做曲线运动,所受摩擦力大小为μmg,路程为s,此过程中摩擦力做功该如何求呢
微元法
变力做功的求法
3
W=W1+W2+W3+…=-μmg(Δs1+Δs2+Δs3+…)=-μmgs
W1=-μmgΔs1
W2=-μmgΔs2
W3=-μmgΔs3
……
例1 在水平面上有一弯曲的槽道AB,由半径分别为 和R的两个半圆构成.如图2所示,现用大小恒为F的拉力将一光滑小球从A点拉至B点,若拉力F的方向时时刻刻与小球运动方向相同,则此过程中拉力所做的功为
图2
√
变力做功的求法
3
跳跳杆将人弹起的过程中,弹簧弹力在不断变化,如何求解此过程中弹簧对人做的功?
原长位置
弹簧将人弹起过程中,弹力与位移成线性关系,可以用弹力的平均值乘以位移来计算功:
注意:只有当 F 和 x 成线性关系时,力的平均值才是算术平均值。
平均力法
变力做功的求法
3
F-x 图像和坐标轴围成的面积表示该力的做功。
原长位置
拓展
图像法
变力做功的求法
3
例2 如图3所示,质量为m的物体静止在光滑的水平面上,物体在下列四种变化规律不同的合外力F作用下都通过相同的位移x0,下列说法正确的是
A.甲图和乙图合外力做功相等
B.丙图和丁图合外力做功相等
C.四个图合外力做功均相等
D.四个图中合外力做功最多的是丙图
图3
√
√
变力做功的求法
3
恒力F通过滑轮将物体从A拉到B的过程中,绳子拉力是变力?那又如何求解绳子拉力做功呢?
由于轻绳并不会存储能量,所以恒力F 做功应该等于绳子对物体做的功:
A
B
h
F
α
β
转换法
变力做功的求法
3
汽车在行驶的过程中,发动机的最大功率等于额定功率.
汽车的功率
汽车的牵引力
汽车的瞬时速度
机车启动过程中的功率
反比
正比
正比
思考与讨论
对于公式 P = F v
(1) 当P 一定时,F 和 v 有什么关系?
(2) 当F 一定时,P 和 v 有什么关系?
(3)当v 一定时,F 和 P 有什么关系?
机车启动的两种方式
4
当F=F阻时,
a=0 ,v达到最大
保持vm匀速
瞬时速度v
牵引力F=
v
P
a=
m
F-F阻
↑
↓
↑
↓
↓
vm=
F阻
P
加速度逐渐减小的变加速直线运动
匀速直线运动
以额定功率 P额 启动
结论:在额定功率下,当汽车做匀速运动时,速度最大.
机车启动的两种方式
4
当F=F阻时,
a=0 ,v达到最大
保持vm匀速
瞬时速度v
牵引力F=
v
P
a=
m
F-F阻
↑
↓
↑
↓
↓
vm=
F阻
P
加速度逐渐减小的变加速直线运动
匀速直线运动
以额定功率 P额 启动
结论:在额定功率下,当汽车做匀速运动时,速度最大.
机车启动的两种方式
4
变加速
匀速
vm
v
t
O
变加速
匀速
vm
v
t
O
t
Pm
P
t
O
f阻
F
t
O
t
a
t
O
t
机车启动的两种方式
4
以额定功率 P额 启动
例3 在水平路面上运动的汽车的额定功率为100 kW,质量为10 t,设阻力恒定,且为车重力的0.1倍(g取10 m/s2),则:
(1)若汽车以不变的额定功率从静止启动,汽车的加速度如何变化?
解析 若汽车以不变的额定功率从静止启动,v变大,
由P额=Fv知,牵引力F减小,
根据牛顿第二定律有F-Ff=ma,可知汽车的加速度逐渐减小到零.
机车启动的两种方式
4
例3 在水平路面上运动的汽车的额定功率为100 kW,质量为10 t,设阻力恒定,且为车重力的0.1倍(g取10 m/s2),则:
机车启动的两种方式
4
(2)当汽车的加速度为2 m/s2时,速度为多大?
解析 F-Ff=ma1
P额=Fv1
例3 在水平路面上运动的汽车的额定功率为100 kW,质量为10 t,设阻力恒定,且为车重力的0.1倍(g取10 m/s2),则:
机车启动的两种方式
4
(3)汽车在运动过程中所能达到的最大速度的大小是多少?
解析 当汽车速度达到最大时,a2=0,F′=Ff,P=P额,
牵引力F牵一定
匀加速直线运动
达到最大速度 vm
变加速直线运动
P < P额,继续匀加速
v F
a
保持 P额 继续加速
达到P额 时速度
F > f阻
速度 v
功率 P
先匀加速再变加速最后匀速,当 F = f阻 时速度最大
v = at
加速度恒定
机车启动的两种方式
4
以恒定牵引力启动
v
t
O
t1
匀速
变加速
匀加速
v1
vm
t2
Pm
P
t
O
F
t
O
a
t
O
f阻
t1
t2
t1
t1
t2
以额定功率 P额 启动
机车启动的两种方式
4
例4 一辆汽车在水平路面上由静止启动,在前5 s内做匀加速直线运动,5 s末达到额定功率,之后保持额定功率运动,其v-t图像如图4所示.已知汽车的质量为m=2×103 kg,汽车受到的阻力为车重力的 ,g取10 m/s2,则
A.汽车在前5 s内受到的阻力大小为200 N
B.前5 s内的牵引力大小为6×103 N
C.汽车的额定功率为40 kW
D.汽车的最大速度为20 m/s
图4
√
机车启动的两种方式
4
1、最大速度的求法
2、匀加速启动最长时间的求法
3、瞬时加速度的求法
匀加速的最后速度:
F=ma+f阻
牵引力:
时间:
机车启动的两种方式
4
机车启动过程中几个物理量的求法
一辆汽车的额定功率为 100 kW,质量为 1.0×104 kg,设阻力恒为车重的 0.1 倍,取 g=10 m/s2。
(1) 若汽车保持恒定功率运动,启动后能达到的最大速度是多大?
(2) 若汽车保持以 0.5 m/s2 的加速度匀加速运动,其匀加速运动能维持多长时间?当汽车行驶的速度为 8 m/s 时,汽车的加速度有多大?
课堂练习
5
一辆汽车的额定功率为 100 kW,质量为 1.0×104 kg,设阻力恒为车重的 0.1 倍,取 g=10 m/s2。
(1) 若汽车保持恒定功率运动,启动后能达到的最大速度是多大?
课堂练习
5
一辆汽车的额定功率为 100 kW,质量为 1.0×104 kg,设阻力恒为车重的 0.1 倍,取 g=10 m/s2。
(2) 若汽车保持以 0.5 m/s2 的加速度匀加速运动,其匀加速运动能维持多长时间?当汽车行驶的速度为 8 m/s 时,汽车的加速度有多大?
课堂练习
5
8.1 功和功率
第八章 机械能守恒定律
叉车竖直提升重物时,力的方向与物体的运动方向一致,则力对物体做功为多少?
W=FL
F
L
F
功
1
叉车水平匀速搬运重物时,力的方向与物体的运动方向垂直,则力对物体做功为多少?
F 不做功 即 W=0
L
F
F
功
1
力F做的功W = ?
叉车斜向上匀速搬运重物时,如果力的方向与物体的运动方向成某一角度 α,则力F对物体做功为多少?
F
F
L
α
功
1
思考?
如果力的方向与物体的运动方向成某一角度 α时:
F
L
α
L1=Lcos α
L2=Lsinɑ
WF = FL1= FLcos α
还有别的方法求力F所做的功吗?
结论:W =FLcosα
功
1
思考?
如果力的方向与物体的运动方向成某一角度 α时:
F
α
结论:W =FLcosα
L
F2=Fsinɑ
F1=Fcosɑ
WF = WF1 = F1L= FLcosɑ
功
1
W=F L cosα
力F对物体做的功
力的大小
位移的大小
力与位移的方向的夹角
功的定义式为:
力对物体所做的功,等于力的大小、位移的大小、力与位移夹角的余弦这三者的乘积.
功是一个标量.在国际单位制中单位是焦耳,简称焦,符号是J.
1J等于1N的力使物体在力的方向上发生1m的位移时所做的功.
1J=1N×1m=1N m
l
F
α
功
1
辨认力的方向与位移方向的夹角
450
F
L
甲
答案:450
450
F
L
乙
答案:1350
450
F
L
丙
答案:450
450
F
L
丁
答案: 1350
方法:将力、位移矢量的箭尾移到同一个作用点上。
功
1
思考?
例1.一个质量为150kg的物体,受到与水平方向成α=37°角的斜向右上方的拉力F1=500N的作用,在水平地面上移动的距离为L=5m,物体与地面间的滑动摩擦力F2=100N,求拉力F1和滑动摩擦力F2做的功?
F1
37°
F2
v
解析:拉力F1对物体所做的功为:W1=F1Lcosα1= F1Lcos37°= 2000J
摩擦力F2对物体所做的功为:W2=F2Lcosα2= F2Lcos180°= –500J
矢量的正、负表示的是方向.功是标量,它的正、负表示什么意思呢?
功
1
思考?
某力对物体做负功,往往说成“物体克服某力做功”(取绝对值),两种说法的意义是等同的。
时,cosα>0,
W>0 力对物体做正功,
促进物体的运动.
时,cosα<0,
W<0力对物体做负功,
阻碍物体的运动.
时,cosα=0,
W =0 力对物体不做功.
功
1
例2.一个质量m=150kg的雪撬,受到与水平方向成θ=37 °角斜向上方的拉力F=500N,在水平地面上移动的距离L=5m.物体与地面间的滑动摩擦力F阻=100N.求力对物体所做的总功.
v
F
θ
FN
G
F阻
W拉=FLcosθ=FLcos37°
阻力做的功
W阻=F阻L cos180°=- F阻L
代入数据,得 W合=1500 J
W合=W拉+W阻=FL cos37°-F阻L
力做的总功
拉力F做的功
解:重力和支持力与运动方向垂直,对物体不做功
思考分析:(1)物体受力情况如何?(2)各个力做功如何?
功
1
例2.一个质量m=150kg的雪撬,受到与水平方向成θ=37 °角斜向上方的拉力F=500N,在水平地面上移动的距离L=5m.物体与地面间的滑动摩擦力F阻=100N.求力对物体所做的总功.
功
1
思考分析:
(1)物体受力情况如何?
(2)物体所受合力是多少?
(3)合力做功多少?
还有其他方法吗?
例2.一个质量m=150kg的雪撬,受到与水平方向成θ=37 °角斜向上方的拉力F=500N,在水平地面上移动的距离L=5m.物体与地面间的滑动摩擦力F阻=100N.求力对物体所做的总功.
功
1
v
F
θ
FN
G
F阻
F1=Fcosθ
代入数据,得 W合=1500 J
W合=F合 L cos0°= (Fcos θ - F阻)L
力对雪橇做的总功
F1
F2
F2=Fsinθ
F合=F1 -F阻= Fcosθ- F阻
解:
总功的求法
W总=W1+W2+W3+
1、功是标量
故合力的功(即总功)就等于各分力做功的代数和:
W总=F合 Lcos α
2、力是矢量
故可以先求合力,再求合力做的功:
功
1
例3 (多选)质量为m的物体,静止在倾角为θ的斜面上,斜面沿水平方向向右匀速移动了距离l,如图7所示.物体始终相对斜面静止,则下列说法正确的是
A.重力对物体做正功
B.合力对物体做功为零
C.摩擦力对物体做负功
D.支持力对物体做正功
√
图7
√
√
功
1
一台耕地机一天能耕地约 20亩田地
一头牛一天能耕地 5 亩 田地
谁做功更快?
定义:功与完成这些功所用时间的比值,叫作功率。
公式:
1 W=1 J/s
物理意义:反映物体做功的快慢。
单位:瓦特(国际单位制),简称瓦,符号是 W
功率是标量
功率
2
长时间运动时人的功率为数10W,优秀运动员可达1kW
长时间运动马的功率为数百瓦
鲸游动时功率可达350kW
小汽车的功率为数十千瓦至两百千瓦
高速列车的功率可达数万kW
万吨豪华游轮的功率可达1万kW以上
功率
2
W=Fl
P=Fv
P=
t
Fl
v=
t
l
P =
t
W
若力与位移的方向在同一直线:
关于功率的另一种表达形式
若力与位移的方向成某一角度 α 时 :
W=Flcosα
P=Fvcosα
P=
t
Flcosα
v=
t
l
P=
t
W
功率
2
v
F
α
v1
v2
F
α
v
F2
F1
P=vFcos α
P=Fvcos α
对公式:P=Fvcos α的理解
功率
2
平均功率:描述在一段时间内做功的平均快慢
瞬时功率:表示在某一时刻做功的快慢
讨论:
分别可以用哪个公式求平均功率和瞬时功率?
平均功率和瞬时功率
(1)求平均功率
(v是平均速度)
(2)求瞬时功率
(v是瞬时速度)
比较常用
(对应一段时间或一个过程)
(对应一个时刻或一个位置)
功率
2
例1 关于功率,下列说法正确的是
√
功率
2
例2 某人用同一水平力F先后两次拉同一物体,第一次使此物体从静止开始在光滑水平面上前进l距离,第二次使此物体从静止开始在粗糙水平面上前进l距离.若先后两次拉力做的功分别为W1和W2,拉力做功的平均功率分别为P1和P2,则
A.W1=W2,P1=P2 B.W1=W2,P1>P2
C.W1>W2,P1>P2 D.W1>W2,P1=P2
√
功率
2
例3 如图1所示,质量为m=2 kg的木块在倾角θ=37°的足够长的固定斜面上由静止开始下滑,木块与斜面间的动摩擦因数为μ=0.5,已知:sin 37°=0.6,cos 37°=0.8,g取10 m/s2,求:
(1)前2 s内重力做的功;
图1
功率
2
解析 木块下滑过程中,由牛顿第二定律得:
mgsin θ-μmgcos θ=ma
联立解得:x=4 m,a=2 m/s2
所以重力在前2 s内做的功为W=mgsin θ·x=2×10×0.6×4 J=48 J;
例3 如图1所示,质量为m=2 kg的木块在倾角θ=37°的足够长的固定斜面上由静止开始下滑,木块与斜面间的动摩擦因数为μ=0.5,已知:sin 37°=0.6,cos 37°=0.8,g取10 m/s2,求:
(2)前2 s内重力的平均功率;
图1
功率
2
例3 如图1所示,质量为m=2 kg的木块在倾角θ=37°的足够长的固定斜面上由静止开始下滑,木块与斜面间的动摩擦因数为μ=0.5,已知:sin 37°=0.6,cos 37°=0.8,g取10 m/s2,求:
图1
功率
2
(3)2 s末重力的瞬时功率.
解析 木块在2 s末的速度大小为
v=at=2×2 m/s=4 m/s
2 s末重力的瞬时功率为
P=mgsin θ·v=2×10×0.6×4 W=48 W.
想一想,物体在水平面上做曲线运动,所受摩擦力大小为μmg,路程为s,此过程中摩擦力做功该如何求呢
微元法
变力做功的求法
3
W=W1+W2+W3+…=-μmg(Δs1+Δs2+Δs3+…)=-μmgs
W1=-μmgΔs1
W2=-μmgΔs2
W3=-μmgΔs3
……
例1 在水平面上有一弯曲的槽道AB,由半径分别为 和R的两个半圆构成.如图2所示,现用大小恒为F的拉力将一光滑小球从A点拉至B点,若拉力F的方向时时刻刻与小球运动方向相同,则此过程中拉力所做的功为
图2
√
变力做功的求法
3
跳跳杆将人弹起的过程中,弹簧弹力在不断变化,如何求解此过程中弹簧对人做的功?
原长位置
弹簧将人弹起过程中,弹力与位移成线性关系,可以用弹力的平均值乘以位移来计算功:
注意:只有当 F 和 x 成线性关系时,力的平均值才是算术平均值。
平均力法
变力做功的求法
3
F-x 图像和坐标轴围成的面积表示该力的做功。
原长位置
拓展
图像法
变力做功的求法
3
例2 如图3所示,质量为m的物体静止在光滑的水平面上,物体在下列四种变化规律不同的合外力F作用下都通过相同的位移x0,下列说法正确的是
A.甲图和乙图合外力做功相等
B.丙图和丁图合外力做功相等
C.四个图合外力做功均相等
D.四个图中合外力做功最多的是丙图
图3
√
√
变力做功的求法
3
恒力F通过滑轮将物体从A拉到B的过程中,绳子拉力是变力?那又如何求解绳子拉力做功呢?
由于轻绳并不会存储能量,所以恒力F 做功应该等于绳子对物体做的功:
A
B
h
F
α
β
转换法
变力做功的求法
3
汽车在行驶的过程中,发动机的最大功率等于额定功率.
汽车的功率
汽车的牵引力
汽车的瞬时速度
机车启动过程中的功率
反比
正比
正比
思考与讨论
对于公式 P = F v
(1) 当P 一定时,F 和 v 有什么关系?
(2) 当F 一定时,P 和 v 有什么关系?
(3)当v 一定时,F 和 P 有什么关系?
机车启动的两种方式
4
当F=F阻时,
a=0 ,v达到最大
保持vm匀速
瞬时速度v
牵引力F=
v
P
a=
m
F-F阻
↑
↓
↑
↓
↓
vm=
F阻
P
加速度逐渐减小的变加速直线运动
匀速直线运动
以额定功率 P额 启动
结论:在额定功率下,当汽车做匀速运动时,速度最大.
机车启动的两种方式
4
当F=F阻时,
a=0 ,v达到最大
保持vm匀速
瞬时速度v
牵引力F=
v
P
a=
m
F-F阻
↑
↓
↑
↓
↓
vm=
F阻
P
加速度逐渐减小的变加速直线运动
匀速直线运动
以额定功率 P额 启动
结论:在额定功率下,当汽车做匀速运动时,速度最大.
机车启动的两种方式
4
变加速
匀速
vm
v
t
O
变加速
匀速
vm
v
t
O
t
Pm
P
t
O
f阻
F
t
O
t
a
t
O
t
机车启动的两种方式
4
以额定功率 P额 启动
例3 在水平路面上运动的汽车的额定功率为100 kW,质量为10 t,设阻力恒定,且为车重力的0.1倍(g取10 m/s2),则:
(1)若汽车以不变的额定功率从静止启动,汽车的加速度如何变化?
解析 若汽车以不变的额定功率从静止启动,v变大,
由P额=Fv知,牵引力F减小,
根据牛顿第二定律有F-Ff=ma,可知汽车的加速度逐渐减小到零.
机车启动的两种方式
4
例3 在水平路面上运动的汽车的额定功率为100 kW,质量为10 t,设阻力恒定,且为车重力的0.1倍(g取10 m/s2),则:
机车启动的两种方式
4
(2)当汽车的加速度为2 m/s2时,速度为多大?
解析 F-Ff=ma1
P额=Fv1
例3 在水平路面上运动的汽车的额定功率为100 kW,质量为10 t,设阻力恒定,且为车重力的0.1倍(g取10 m/s2),则:
机车启动的两种方式
4
(3)汽车在运动过程中所能达到的最大速度的大小是多少?
解析 当汽车速度达到最大时,a2=0,F′=Ff,P=P额,
牵引力F牵一定
匀加速直线运动
达到最大速度 vm
变加速直线运动
P < P额,继续匀加速
v F
a
保持 P额 继续加速
达到P额 时速度
F > f阻
速度 v
功率 P
先匀加速再变加速最后匀速,当 F = f阻 时速度最大
v = at
加速度恒定
机车启动的两种方式
4
以恒定牵引力启动
v
t
O
t1
匀速
变加速
匀加速
v1
vm
t2
Pm
P
t
O
F
t
O
a
t
O
f阻
t1
t2
t1
t1
t2
以额定功率 P额 启动
机车启动的两种方式
4
例4 一辆汽车在水平路面上由静止启动,在前5 s内做匀加速直线运动,5 s末达到额定功率,之后保持额定功率运动,其v-t图像如图4所示.已知汽车的质量为m=2×103 kg,汽车受到的阻力为车重力的 ,g取10 m/s2,则
A.汽车在前5 s内受到的阻力大小为200 N
B.前5 s内的牵引力大小为6×103 N
C.汽车的额定功率为40 kW
D.汽车的最大速度为20 m/s
图4
√
机车启动的两种方式
4
1、最大速度的求法
2、匀加速启动最长时间的求法
3、瞬时加速度的求法
匀加速的最后速度:
F=ma+f阻
牵引力:
时间:
机车启动的两种方式
4
机车启动过程中几个物理量的求法
一辆汽车的额定功率为 100 kW,质量为 1.0×104 kg,设阻力恒为车重的 0.1 倍,取 g=10 m/s2。
(1) 若汽车保持恒定功率运动,启动后能达到的最大速度是多大?
(2) 若汽车保持以 0.5 m/s2 的加速度匀加速运动,其匀加速运动能维持多长时间?当汽车行驶的速度为 8 m/s 时,汽车的加速度有多大?
课堂练习
5
一辆汽车的额定功率为 100 kW,质量为 1.0×104 kg,设阻力恒为车重的 0.1 倍,取 g=10 m/s2。
(1) 若汽车保持恒定功率运动,启动后能达到的最大速度是多大?
课堂练习
5
一辆汽车的额定功率为 100 kW,质量为 1.0×104 kg,设阻力恒为车重的 0.1 倍,取 g=10 m/s2。
(2) 若汽车保持以 0.5 m/s2 的加速度匀加速运动,其匀加速运动能维持多长时间?当汽车行驶的速度为 8 m/s 时,汽车的加速度有多大?
课堂练习
5
