冀教版数学八年级下册同步课件:19.4 第1课时 图形的平移与坐标变化(共25张PPT)
文档属性
| 名称 | 冀教版数学八年级下册同步课件:19.4 第1课时 图形的平移与坐标变化(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 301.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 12:39:31 | ||
图片预览




文档简介
(共25张PPT)
第十九章 平面直角坐标系
19.4 第1课时 图形的平移与坐标变化
想一想:图形做的是什么运动?
A
B
情景导入
今天我们探究在直角坐标系中平移图形......
x
y
知识回顾
问题1 你还记得什么叫平移吗?
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
问题2 图形平移有什么性质?
(2)经过平移后,对应点所连的线段平行(或共线)且相等.
(1)平移不改变图形的形状和大小,只改变形图形的位置;
获取新知
一起探究
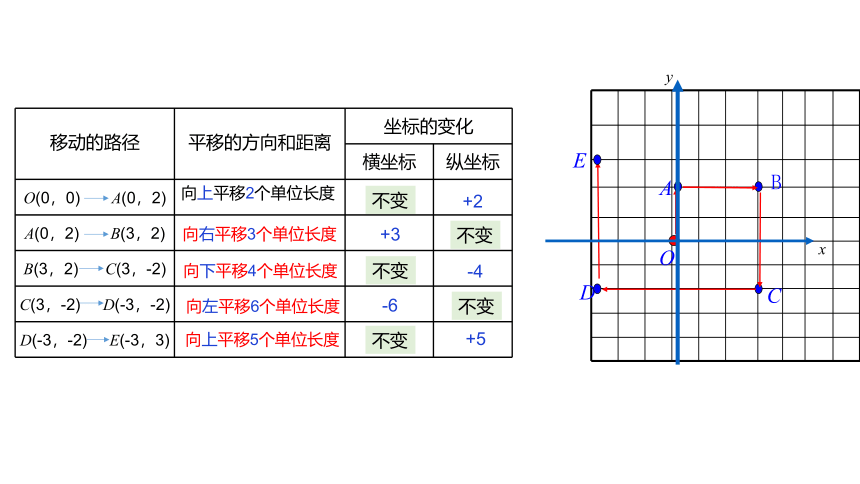
1.在坐标平面上,一只蚂蚁从原点出发,爬行的路径如图所示:
(1)找出A,B,C,D,E这五个点的坐标.
(2)指出蚂蚁在各条线段上的爬行的方向和距离,并填写下表.
D
C
B
A
E
O
y
x
知识点
点的平移与点的坐标变化
1
移动的路径 平移的方向和距离 坐标的变化 横坐标 纵坐标
O(0,0) A(0,2) 向上平移2个单位长度
A(0,2) B(3,2)
B(3,2) C(3,-2)
C(3,-2) D(-3,-2)
D(-3,-2) E(-3,3)
向右平移3个单位长度
向下平移4个单位长度
向左平移6个单位长度
向上平移5个单位长度
不变
+2
不变
+3
不变
-4
不变
-6
不变
+5
D
C
B
A
E
O
y
x
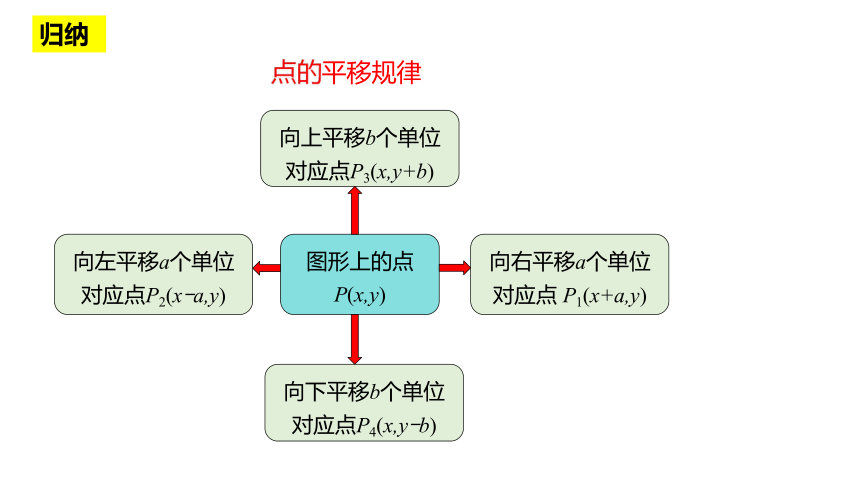
向左平移a个单位对应点P2(x-a,y)
向右平移a个单位对应点 P1(x+a,y)
向上平移b个单位对应点P3(x,y+b)
向下平移b个单位对应点P4(x,y-b)
图形上的点P(x,y)
点的平移规律
归纳
巩固练习
1.在平面直角坐标系中,点P(-2,-3)向左平移1个单位长度,再向上平移3个单位长度,所得到的点的坐标为__________.
(-3,0)
2.将点P向左平移2个单位长度,再向上平移1个单位长度得到P'(-1,3),则点P的坐标为__________.
(-1,2)
分析:
横坐标减1,纵坐标加3
分析:
可理解为将点P'向右平移2个单位长度,再向下平移1个单位长度得到点P.
口 诀
上下平移
左右平移
上加下减横不变
左减右加纵不变
例题讲解
例 如下图,在平面直角坐标系中,长方
形ABCD各顶点的坐标分别为A(-2,1),
B(2,1),C(2,3),D(-2,3),长方
形ABCD沿x轴的方向向右平移5个单位长
度,得到长方形A1B1C1D1.
(1)请写出它的各顶点坐标.
(2)指出对应顶点坐标的变化规律.
y
-2
2
4
6
8
2
4
-2
-4
O
A
B
C
D
A1
B1
C1
D1
x
y
-2
2
4
6
8
2
4
-2
-4
O
A
B
C
D
A1
B1
C1
D1
解:长方形A1B1C1D1各顶点的坐标为:
A1(3,1),B1(7,1),
C1(7,3) ,D1(3,3).
各顶点移动的方向一致,移动的距离
都是5个单位长度.
变化规律:
长方形A1B1C1D1各顶点的坐标是长方形ABCD各顶点的横坐标都加5得到,纵坐标不变而得到的.
x
y
-2
2
4
6
8
2
4
-2
-4
O
A
B
C
D
A2
B2
C2
D2
1.在下图中,将长方形ABCD沿y轴的方向向下平移4个单位长度,画出平移后的长方形A2B2C2D2,写出其各点的坐标,并说出平移前后对应顶点的变化规律.
A2(-2,-3);B2(2,-3);
C2(2,-1);D2(-2,-1)
变化规律:
长方形A1B1C1D1各顶点的坐标是长方形ABCD各顶点的横坐标不变,纵坐标都减4得到.
获取新知
x
y
-2
2
4
6
8
2
4
-2
-4
O
A
B
C
D
A3
B3
C3
D3
2.如果将长方形ABCD先沿x轴向右平移6个单位长度,再沿y轴向下平移5个单位长度,画出平移后的长方形A3B3C3D3,写出各顶点的坐标,指出其中的对应顶点的变化规律.
A3(4,-4);B3(8,-4);
C3(8,-2);D3(4,-2)
变化规律:
长方形A1B1C1D1各顶点的坐标是长方形ABCD各顶点的横坐标加6,纵坐标都减5得到.
在直角坐标系中,将一个图形沿坐标轴方向平移时,各顶点是否具有相同的变化规律呢?
思考:
因为图形平移时,图形上所有点的平移方向和距离是一样的.
是
(1)原图形向左(右)平移a个单位长度:(a>0)
向右平移a个单位
(2)原图形向上(下)平移b个单位长度:(b>0)
原图形上的点P(x,y)
向左平移a个单位
原图形上的点P (x,y)
P1(x+a,y)
P2(x-a,y)
向上平移b个单位
原图形上的点P(x,y)
向下平移b个单位
原图形上的点P(x,y)
P3(x,y+b)
P4(x,y-b)
归纳
3
2
1
-2
-1
-3
4
y
A
B
C
-4
A1
C1
B1
例2 如图, △ABC在直角坐标系内,向右平移5个单位长度后得到△A1B1C1.
(1)△ABC与△A1B1C1各顶点的坐标有怎样的变化?
-3
-2
O
1
2
3
4
x
解:平移后的对应点的横坐标
增加了5,纵坐标不变.
例题讲解
3
2
1
-2
-1
-3
4
y
A
B
C
-4
A2
(2)如果将△ABC的所有点的横坐标不变,纵坐标减4后,得到△A2B2C2,则两个三角形的形状及位置有何关系?
-3
-2
C2
B2
O
1
2
3
4
x
-1
解:两个三角形的形状相同,△ABC向下平移4个单位长度后得到△A2B2C2.
图形变化与坐标变化的区别
图形变化
坐标变化
图形上、下、左、右平移
横、纵坐标的加、减
图形
数字
归纳
数形结合思想
随堂演练
1. 在平面直角坐标系中,将三角形各顶点的纵坐标都减去1,横坐标保持不变,所得图形与原图形相比是( )
A.向下平移了1个单位长度
B.向上平移了1个单位长度
C.向左平移了1个单位长度
D.向右平移了1个单位长度
A
2. 如图,在平面直角坐标系中,将点M(2,1)向下平移2个单位长度得到点N,则点N的坐标为( )
A.(2,-1)
B.(2,3)
C.(0,1)
D.(4,1)
A
3. 如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P(a,b),则点P在A′B′上的对应点P′的坐标为( )
A.(a-2,b+3)
B.(a-2,b-3)
C.(a+2,b+3)
D.(a+2,b-3)
A
4. 如图,在平面直角坐标系中,三角形ABC的顶点都在格点上,其中,C点坐标为(1,2).
(1)写出点A,B的坐标:
A(____,____),B(____,____);
(2)将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度,得到三角形A′B′C′,则三角形A′B′C′的三个顶点坐标分别是A′(____,____),B′(____,____),C′(____,____);
(3)三角形ABC的面积为_____.
2 -1
4 3
0 0
2 4
-1 3
5
5. 在平面直角坐标系中,△ABC的位置如图所示,把△ABC平移后,△ABC内任意点P(x,y)的对应点为P'(x+3,y-4).
(1)画出平移后的图形;
(2)△ABC是经过怎样的平移得到△A'B'C'的
解:(1)如图所示,△A'B'C'即为所求.
(2)△ABC先向右平移3个单位长度,再向下平移4个单位长度可以得△A'B'C'.
课堂小结
图形在坐标系中的平移
沿x轴平移
沿y轴平移
纵坐标不变
横坐标加上一个正数,向右平移
横坐标减去一个正数,向左平移
横坐标不变
纵坐标加上一个正数,向上平移
纵坐标减去一个正数,向下平移
第十九章 平面直角坐标系
19.4 第1课时 图形的平移与坐标变化
想一想:图形做的是什么运动?
A
B
情景导入
今天我们探究在直角坐标系中平移图形......
x
y
知识回顾
问题1 你还记得什么叫平移吗?
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
问题2 图形平移有什么性质?
(2)经过平移后,对应点所连的线段平行(或共线)且相等.
(1)平移不改变图形的形状和大小,只改变形图形的位置;
获取新知
一起探究
1.在坐标平面上,一只蚂蚁从原点出发,爬行的路径如图所示:
(1)找出A,B,C,D,E这五个点的坐标.
(2)指出蚂蚁在各条线段上的爬行的方向和距离,并填写下表.
D
C
B
A
E
O
y
x
知识点
点的平移与点的坐标变化
1
移动的路径 平移的方向和距离 坐标的变化 横坐标 纵坐标
O(0,0) A(0,2) 向上平移2个单位长度
A(0,2) B(3,2)
B(3,2) C(3,-2)
C(3,-2) D(-3,-2)
D(-3,-2) E(-3,3)
向右平移3个单位长度
向下平移4个单位长度
向左平移6个单位长度
向上平移5个单位长度
不变
+2
不变
+3
不变
-4
不变
-6
不变
+5
D
C
B
A
E
O
y
x
向左平移a个单位对应点P2(x-a,y)
向右平移a个单位对应点 P1(x+a,y)
向上平移b个单位对应点P3(x,y+b)
向下平移b个单位对应点P4(x,y-b)
图形上的点P(x,y)
点的平移规律
归纳
巩固练习
1.在平面直角坐标系中,点P(-2,-3)向左平移1个单位长度,再向上平移3个单位长度,所得到的点的坐标为__________.
(-3,0)
2.将点P向左平移2个单位长度,再向上平移1个单位长度得到P'(-1,3),则点P的坐标为__________.
(-1,2)
分析:
横坐标减1,纵坐标加3
分析:
可理解为将点P'向右平移2个单位长度,再向下平移1个单位长度得到点P.
口 诀
上下平移
左右平移
上加下减横不变
左减右加纵不变
例题讲解
例 如下图,在平面直角坐标系中,长方
形ABCD各顶点的坐标分别为A(-2,1),
B(2,1),C(2,3),D(-2,3),长方
形ABCD沿x轴的方向向右平移5个单位长
度,得到长方形A1B1C1D1.
(1)请写出它的各顶点坐标.
(2)指出对应顶点坐标的变化规律.
y
-2
2
4
6
8
2
4
-2
-4
O
A
B
C
D
A1
B1
C1
D1
x
y
-2
2
4
6
8
2
4
-2
-4
O
A
B
C
D
A1
B1
C1
D1
解:长方形A1B1C1D1各顶点的坐标为:
A1(3,1),B1(7,1),
C1(7,3) ,D1(3,3).
各顶点移动的方向一致,移动的距离
都是5个单位长度.
变化规律:
长方形A1B1C1D1各顶点的坐标是长方形ABCD各顶点的横坐标都加5得到,纵坐标不变而得到的.
x
y
-2
2
4
6
8
2
4
-2
-4
O
A
B
C
D
A2
B2
C2
D2
1.在下图中,将长方形ABCD沿y轴的方向向下平移4个单位长度,画出平移后的长方形A2B2C2D2,写出其各点的坐标,并说出平移前后对应顶点的变化规律.
A2(-2,-3);B2(2,-3);
C2(2,-1);D2(-2,-1)
变化规律:
长方形A1B1C1D1各顶点的坐标是长方形ABCD各顶点的横坐标不变,纵坐标都减4得到.
获取新知
x
y
-2
2
4
6
8
2
4
-2
-4
O
A
B
C
D
A3
B3
C3
D3
2.如果将长方形ABCD先沿x轴向右平移6个单位长度,再沿y轴向下平移5个单位长度,画出平移后的长方形A3B3C3D3,写出各顶点的坐标,指出其中的对应顶点的变化规律.
A3(4,-4);B3(8,-4);
C3(8,-2);D3(4,-2)
变化规律:
长方形A1B1C1D1各顶点的坐标是长方形ABCD各顶点的横坐标加6,纵坐标都减5得到.
在直角坐标系中,将一个图形沿坐标轴方向平移时,各顶点是否具有相同的变化规律呢?
思考:
因为图形平移时,图形上所有点的平移方向和距离是一样的.
是
(1)原图形向左(右)平移a个单位长度:(a>0)
向右平移a个单位
(2)原图形向上(下)平移b个单位长度:(b>0)
原图形上的点P(x,y)
向左平移a个单位
原图形上的点P (x,y)
P1(x+a,y)
P2(x-a,y)
向上平移b个单位
原图形上的点P(x,y)
向下平移b个单位
原图形上的点P(x,y)
P3(x,y+b)
P4(x,y-b)
归纳
3
2
1
-2
-1
-3
4
y
A
B
C
-4
A1
C1
B1
例2 如图, △ABC在直角坐标系内,向右平移5个单位长度后得到△A1B1C1.
(1)△ABC与△A1B1C1各顶点的坐标有怎样的变化?
-3
-2
O
1
2
3
4
x
解:平移后的对应点的横坐标
增加了5,纵坐标不变.
例题讲解
3
2
1
-2
-1
-3
4
y
A
B
C
-4
A2
(2)如果将△ABC的所有点的横坐标不变,纵坐标减4后,得到△A2B2C2,则两个三角形的形状及位置有何关系?
-3
-2
C2
B2
O
1
2
3
4
x
-1
解:两个三角形的形状相同,△ABC向下平移4个单位长度后得到△A2B2C2.
图形变化与坐标变化的区别
图形变化
坐标变化
图形上、下、左、右平移
横、纵坐标的加、减
图形
数字
归纳
数形结合思想
随堂演练
1. 在平面直角坐标系中,将三角形各顶点的纵坐标都减去1,横坐标保持不变,所得图形与原图形相比是( )
A.向下平移了1个单位长度
B.向上平移了1个单位长度
C.向左平移了1个单位长度
D.向右平移了1个单位长度
A
2. 如图,在平面直角坐标系中,将点M(2,1)向下平移2个单位长度得到点N,则点N的坐标为( )
A.(2,-1)
B.(2,3)
C.(0,1)
D.(4,1)
A
3. 如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P(a,b),则点P在A′B′上的对应点P′的坐标为( )
A.(a-2,b+3)
B.(a-2,b-3)
C.(a+2,b+3)
D.(a+2,b-3)
A
4. 如图,在平面直角坐标系中,三角形ABC的顶点都在格点上,其中,C点坐标为(1,2).
(1)写出点A,B的坐标:
A(____,____),B(____,____);
(2)将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度,得到三角形A′B′C′,则三角形A′B′C′的三个顶点坐标分别是A′(____,____),B′(____,____),C′(____,____);
(3)三角形ABC的面积为_____.
2 -1
4 3
0 0
2 4
-1 3
5
5. 在平面直角坐标系中,△ABC的位置如图所示,把△ABC平移后,△ABC内任意点P(x,y)的对应点为P'(x+3,y-4).
(1)画出平移后的图形;
(2)△ABC是经过怎样的平移得到△A'B'C'的
解:(1)如图所示,△A'B'C'即为所求.
(2)△ABC先向右平移3个单位长度,再向下平移4个单位长度可以得△A'B'C'.
课堂小结
图形在坐标系中的平移
沿x轴平移
沿y轴平移
纵坐标不变
横坐标加上一个正数,向右平移
横坐标减去一个正数,向左平移
横坐标不变
纵坐标加上一个正数,向上平移
纵坐标减去一个正数,向下平移
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
