冀教版数学八年级下册同步课件:20.3 函数的表示(共22张PPT)
文档属性
| 名称 | 冀教版数学八年级下册同步课件:20.3 函数的表示(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 323.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 12:46:26 | ||
图片预览





文档简介
(共22张PPT)
第二十章 函数
20.3 函数的表示
知识回顾
函数的三种表示法:
①图像法
②列表法
③表达式法
课堂导入
函数有不同的表达方式,可用来表达不同的问题情境,帮助我们分析和解决问题.
我们知道,用表达式、图像和数值表都可以表示变量之间的关系.现在,我们对这些表示方法作进一步的探究.
获取新知
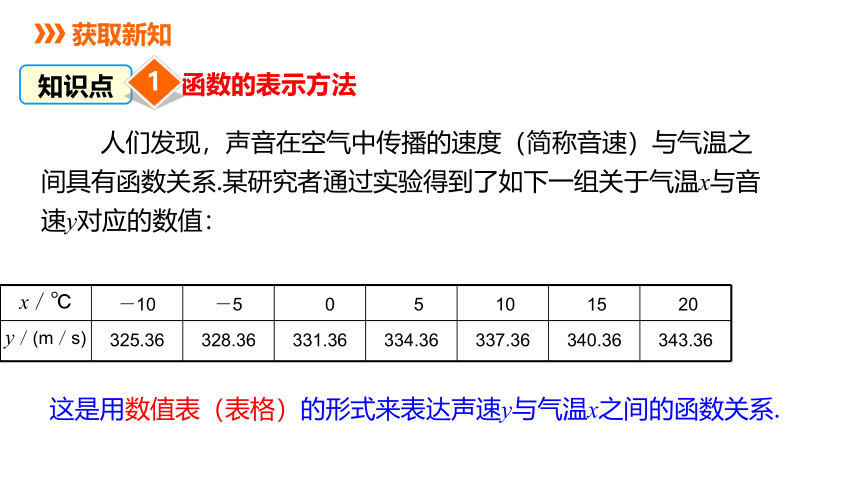
人们发现,声音在空气中传播的速度(简称音速)与气温之间具有函数关系.某研究者通过实验得到了如下一组关于气温x与音速y对应的数值:
x/℃ -10 -5 0 5 10 15 20
y/(m/s) 325.36 328.36 331.36 334.36 337.36 340.36 343.36
这是用数值表(表格)的形式来表达声速y与气温x之间的函数关系.
知识点
函数的表示方法
1
做一做
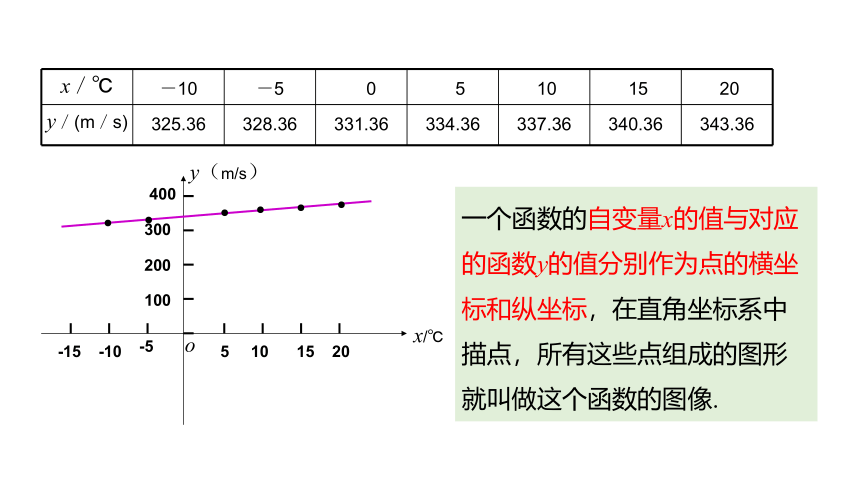
1. 以横轴表示气温,每5℃为一个单位,纵轴表示声速,每100m/s为一个单位长度,建立直角坐标系.以表格中给出的气温和声速的数值为点的横坐标和纵坐标,在直角坐标系中描点,连线(用平滑的曲线连点)画出图形.
y(m/s)
100
200
300
400
o
-15
-10
-5
5
10
15
20
x/℃
●
●
●
●
●
●
一个函数的自变量x的值与对应的函数y的值分别作为点的横坐标和纵坐标,在直角坐标系中描点,所有这些点组成的图形就叫做这个函数的图像.
x/℃ -10 -5 0 5 10 15 20
y/(m/s) 325.36 328.36 331.36 334.36 337.36 340.36 343.36
2.观察表格中数值,不难发现:气温每升高(或降低)5℃,对应的声速增加(或减少)3m/s.根据这个特点,求声速y(m/s)与气温x( ℃)之间的函数关系式.
y关于x的函数关系式为:
x/℃ -10 -5 0 5 10 15 20
y/(m/s) 325.36 328.36 331.36 334.36 337.36 340.36 343.36
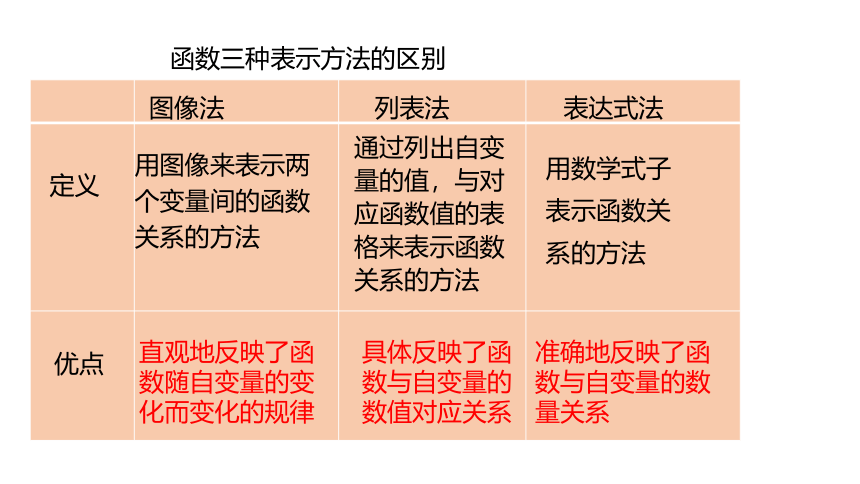
列表法
表达式法
图像法
定义
优点
通过列出自变量的值,与对应函数值的表格来表示函数关系的方法
具体反映了函数与自变量的数值对应关系
用数学式子表示函数关系的方法
准确地反映了函数与自变量的数量关系
用图像来表示两个变量间的函数关系的方法
直观地反映了函数随自变量的变化而变化的规律
函数三种表示方法的区别
例题讲解
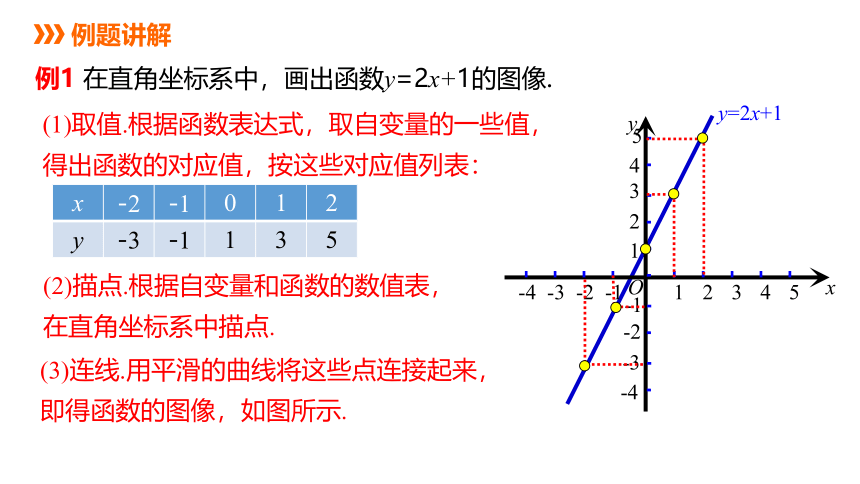
例1 在直角坐标系中,画出函数y=2x+1的图像.
(1)取值.根据函数表达式,取自变量的一些值,得出函数的对应值,按这些对应值列表:
x -2 -1 0 1 2
y -3 -1 1 3 5
(2)描点.根据自变量和函数的数值表,在直角坐标系中描点.
(3)连线.用平滑的曲线将这些点连接起来,即得函数的图像,如图所示.
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=2x+1
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=2x+1
当自变量的值越来越大时,
对应的函数值 .
画出的图像是一条 ,
直线
越来越大
观察
第一步,列表——表中给出一些自变量的值及其 ;
第二步,描点——在平面直角坐标系中,以自变量的值为 ,相应的函数值为 ,描出表格中数值对应的各点;
第三步:连线——按照横坐标 的顺序,
把所描出的各点用 连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
归纳总结
画函数图像的一般步骤:
输入数x
输出结果y
用计算器可以求出任何一个非负数的算术平方根,显示器显示的结果随输入数的变化而变化.设输入数为x显示的结果为y,程序如图所示:
(1)请写出y与x之间的函数关系式,并指出自变量的取值范围.
做一做
(2)根据函数关系式填写表格.
(3)借助这些对应的数值画出这个函数的图像.
y
16
9
4
1
0
x
x
y
0
1
2
3
4
例2 某天7时,小明从家骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校. 下图反映了他骑车的整个过程,结合图像,回答下列问题:
(1)自行车发生故障是在什么时间?此时离家有多远?
从横坐标看出,自行车发生故障的时间是7:05; 从纵坐标看出,此时离家1000m.
知识点
从函数图像获取信息
2
获取新知
(2)修车花了多长时间?修好车后又花了多长时间到达学校?
从横坐标看出,小明修车花了15 min;
小明修好车后又花了10 min到达学校.
(3)小明从家到学校的平均速度是多少?
从纵坐标看出,小明家离学校2100 m;
从横坐标看出, 他在路上共花了30 min,
因此, 他从家到学校的平均速度是
2100 ÷ 30 = 70 (m/min).
如图是丽丽上学骑车途中速度v(千米/时)与时间t(分)的关系图象.
(1)她上学共用了多长时间 最大速度是多少
变式练习
从出发到结束一共用了40分钟,故她上学共用了40分钟,最大速度是20千米/时.
如图是丽丽上学骑车途中速度v(千米/时)与时间t(分)的关系图象.
(2)开始出发的前10分钟她的速度有什么变化 哪段时间匀速行驶 最后10分钟呢
从图象中可以看出:开始出发的前10分钟,表示速度的线是上升的,所以这段时间是加速运动.从第10分钟至第30分钟,表示速度的线是水平的,所以这段时间是匀速运动.最后10分钟,表示速度的线是下降的,所以这段时间是减速运动,直到速度为0.
随堂演练
1. 爷爷在离家900米的公园锻炼后回家,离开公园20分钟后,爷爷停下来与朋友聊天10分钟,接着又走了15分钟回到家中.图中表示爷爷离家的距离y(米)与爷爷离开公园的时间x(分)之间的函数关系的是( )
B
2.在如图所示的计算程序中,y与x之间的函数关系式为 .
y=-2x+4
3.小明同学骑自行车去郊外春游,
如图表示他离家的距离y(km)与所
用的时间x(h)之间关系的函数图象.
(1)根据图象回答:小明到达离
家最远的地方需______h;
(2)小明出发2.5 h后离家_______km;
(3)小明出发__________h后离家12 km.
3
22.5
0.8或5.2
y
5
x
O
-4
-3
-2
-1
1
2
3
4
5
-5
1
2
3
4
-1
-2
-3
-4
-5
6
-6
(2)描点: 在坐标系中描
出对应的点.
(3)连线: 用平滑的曲线把这些点依次连接起来.
(1,-6)
解:(1)列表 :取一些自变量的值,并求出对应的函数值,填入表中.
4.画出函数 - 的图像.
x … -5 -4 -3 -2 -1
y …
1 2 3 4 5 …
…
-6
6
-3
-2
-1.2
-1.5
3
2
1.5
1.2
课堂小结
函数的表示方法
表达式法:准确反映了函数与自变量之间的数量关系
列表法:具体反映了函数与自变量的数值对应关系
图象法:形象反映了函数随自变量的变化而变化的规律
画函数图像步骤:
列表-描点-连线
从函数图像获取信息
第二十章 函数
20.3 函数的表示
知识回顾
函数的三种表示法:
①图像法
②列表法
③表达式法
课堂导入
函数有不同的表达方式,可用来表达不同的问题情境,帮助我们分析和解决问题.
我们知道,用表达式、图像和数值表都可以表示变量之间的关系.现在,我们对这些表示方法作进一步的探究.
获取新知
人们发现,声音在空气中传播的速度(简称音速)与气温之间具有函数关系.某研究者通过实验得到了如下一组关于气温x与音速y对应的数值:
x/℃ -10 -5 0 5 10 15 20
y/(m/s) 325.36 328.36 331.36 334.36 337.36 340.36 343.36
这是用数值表(表格)的形式来表达声速y与气温x之间的函数关系.
知识点
函数的表示方法
1
做一做
1. 以横轴表示气温,每5℃为一个单位,纵轴表示声速,每100m/s为一个单位长度,建立直角坐标系.以表格中给出的气温和声速的数值为点的横坐标和纵坐标,在直角坐标系中描点,连线(用平滑的曲线连点)画出图形.
y(m/s)
100
200
300
400
o
-15
-10
-5
5
10
15
20
x/℃
●
●
●
●
●
●
一个函数的自变量x的值与对应的函数y的值分别作为点的横坐标和纵坐标,在直角坐标系中描点,所有这些点组成的图形就叫做这个函数的图像.
x/℃ -10 -5 0 5 10 15 20
y/(m/s) 325.36 328.36 331.36 334.36 337.36 340.36 343.36
2.观察表格中数值,不难发现:气温每升高(或降低)5℃,对应的声速增加(或减少)3m/s.根据这个特点,求声速y(m/s)与气温x( ℃)之间的函数关系式.
y关于x的函数关系式为:
x/℃ -10 -5 0 5 10 15 20
y/(m/s) 325.36 328.36 331.36 334.36 337.36 340.36 343.36
列表法
表达式法
图像法
定义
优点
通过列出自变量的值,与对应函数值的表格来表示函数关系的方法
具体反映了函数与自变量的数值对应关系
用数学式子表示函数关系的方法
准确地反映了函数与自变量的数量关系
用图像来表示两个变量间的函数关系的方法
直观地反映了函数随自变量的变化而变化的规律
函数三种表示方法的区别
例题讲解
例1 在直角坐标系中,画出函数y=2x+1的图像.
(1)取值.根据函数表达式,取自变量的一些值,得出函数的对应值,按这些对应值列表:
x -2 -1 0 1 2
y -3 -1 1 3 5
(2)描点.根据自变量和函数的数值表,在直角坐标系中描点.
(3)连线.用平滑的曲线将这些点连接起来,即得函数的图像,如图所示.
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=2x+1
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=2x+1
当自变量的值越来越大时,
对应的函数值 .
画出的图像是一条 ,
直线
越来越大
观察
第一步,列表——表中给出一些自变量的值及其 ;
第二步,描点——在平面直角坐标系中,以自变量的值为 ,相应的函数值为 ,描出表格中数值对应的各点;
第三步:连线——按照横坐标 的顺序,
把所描出的各点用 连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
归纳总结
画函数图像的一般步骤:
输入数x
输出结果y
用计算器可以求出任何一个非负数的算术平方根,显示器显示的结果随输入数的变化而变化.设输入数为x显示的结果为y,程序如图所示:
(1)请写出y与x之间的函数关系式,并指出自变量的取值范围.
做一做
(2)根据函数关系式填写表格.
(3)借助这些对应的数值画出这个函数的图像.
y
16
9
4
1
0
x
x
y
0
1
2
3
4
例2 某天7时,小明从家骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校. 下图反映了他骑车的整个过程,结合图像,回答下列问题:
(1)自行车发生故障是在什么时间?此时离家有多远?
从横坐标看出,自行车发生故障的时间是7:05; 从纵坐标看出,此时离家1000m.
知识点
从函数图像获取信息
2
获取新知
(2)修车花了多长时间?修好车后又花了多长时间到达学校?
从横坐标看出,小明修车花了15 min;
小明修好车后又花了10 min到达学校.
(3)小明从家到学校的平均速度是多少?
从纵坐标看出,小明家离学校2100 m;
从横坐标看出, 他在路上共花了30 min,
因此, 他从家到学校的平均速度是
2100 ÷ 30 = 70 (m/min).
如图是丽丽上学骑车途中速度v(千米/时)与时间t(分)的关系图象.
(1)她上学共用了多长时间 最大速度是多少
变式练习
从出发到结束一共用了40分钟,故她上学共用了40分钟,最大速度是20千米/时.
如图是丽丽上学骑车途中速度v(千米/时)与时间t(分)的关系图象.
(2)开始出发的前10分钟她的速度有什么变化 哪段时间匀速行驶 最后10分钟呢
从图象中可以看出:开始出发的前10分钟,表示速度的线是上升的,所以这段时间是加速运动.从第10分钟至第30分钟,表示速度的线是水平的,所以这段时间是匀速运动.最后10分钟,表示速度的线是下降的,所以这段时间是减速运动,直到速度为0.
随堂演练
1. 爷爷在离家900米的公园锻炼后回家,离开公园20分钟后,爷爷停下来与朋友聊天10分钟,接着又走了15分钟回到家中.图中表示爷爷离家的距离y(米)与爷爷离开公园的时间x(分)之间的函数关系的是( )
B
2.在如图所示的计算程序中,y与x之间的函数关系式为 .
y=-2x+4
3.小明同学骑自行车去郊外春游,
如图表示他离家的距离y(km)与所
用的时间x(h)之间关系的函数图象.
(1)根据图象回答:小明到达离
家最远的地方需______h;
(2)小明出发2.5 h后离家_______km;
(3)小明出发__________h后离家12 km.
3
22.5
0.8或5.2
y
5
x
O
-4
-3
-2
-1
1
2
3
4
5
-5
1
2
3
4
-1
-2
-3
-4
-5
6
-6
(2)描点: 在坐标系中描
出对应的点.
(3)连线: 用平滑的曲线把这些点依次连接起来.
(1,-6)
解:(1)列表 :取一些自变量的值,并求出对应的函数值,填入表中.
4.画出函数 - 的图像.
x … -5 -4 -3 -2 -1
y …
1 2 3 4 5 …
…
-6
6
-3
-2
-1.2
-1.5
3
2
1.5
1.2
课堂小结
函数的表示方法
表达式法:准确反映了函数与自变量之间的数量关系
列表法:具体反映了函数与自变量的数值对应关系
图象法:形象反映了函数随自变量的变化而变化的规律
画函数图像步骤:
列表-描点-连线
从函数图像获取信息
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
