冀教版数学八年级下册同步课件:20.4 函数的初步应用(共24张PPT)
文档属性
| 名称 | 冀教版数学八年级下册同步课件:20.4 函数的初步应用(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 309.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 12:51:44 | ||
图片预览








文档简介
(共24张PPT)
第二十章 函数
20.4 函数的初步应用
知识回顾
1.函数概念包含:
(1)两个变量;
(2)两个变量之间的对应关系.
2.函数关系三种表示方法:
(1)表格法
(2)图像法
(3)表达式法
情景导入
摄氏温度和华氏温度都是计量温度单位的,世界上多数国家使用的是摄氏温度,但也有一些国家使用华氏温度.
摄氏温度和华氏温度如何互相转化呢?
获取新知
常用的温度计量标准有两种,一种是摄氏温度(℃),另一种是华氏温度(℉).
想一想:华氏温度与摄氏温度是否具有函数关系呢?
从温度计来看是一个对应一个,那么你能确定它们之间的表达式吗?
知识点
表格法的初步运用
1
一起探究
已知摄氏温度值和华氏温度值有下表所示的对应关系:
摄氏温度/ C 0 10 20 30 40 50
华氏温度/ F 32 50 68 86 104 122
(1)当摄氏温度为30时,华氏温度为多少?
86
摄氏温度/ C 0 10 20 30 40 50
华氏温度/ F 32 50 68 86 104 122
(2)当摄氏温度为36时,由数值表能直接看出华氏温度吗?试写出这两种温度计量之间关系的函数表达式,并求摄氏温度为36时的华氏温度;
观察表格中数据,你发现了什么规律吗?
解:不能由表格直接得出摄氏温度为36时对应的华氏温度.
【分析】观察表格可得,摄氏温度为0°C时,华氏温度为32°F.摄氏温度每增加10°C.华氏温度增加18°F,即摄氏温度增加1°C,华氏温度增加1.8°F.所以,华氏温度=32+1.8×摄氏温度.
若设摄氏温度为t C,华氏温度为f F,则f =1.8t+32.
当t=36时,f=1.8×36+32=96.8.
摄氏温度/ C 0 10 20 30 40 50
华氏温度/ F 32 50 68 86 104 122
(3)当华氏温度为140时,摄氏温度为多少?
【分析】当华氏温度为140时,140=32+1.8×摄氏温度,解方程即可.
解:当f=36时,140=1.8t+32,解得t=60.
得到函数表达式后,任给一个变量值,可确定另一个变量的值.
试着做做
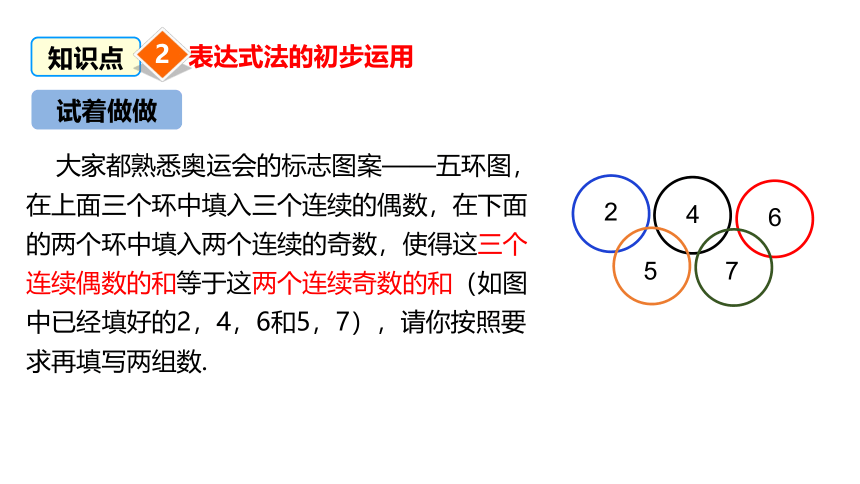
大家都熟悉奥运会的标志图案——五环图,在上面三个环中填入三个连续的偶数,在下面的两个环中填入两个连续的奇数,使得这三个连续偶数的和等于这两个连续奇数的和(如图中已经填好的2,4,6和5,7),请你按照要求再填写两组数.
2
4
6
5
7
知识点
表达式法的初步运用
2
大家谈谈
(1)请和同学交流,各自填写的数组是什么,满足要求的数组有很多吗?
6+8+10=11+13; 10+12+14=17+19; 14+16+18=23+25; 18+20+22=29+31; ……
(2)如果用2x-2,2x,2x+2表示三个连续的偶数,用2y-1,2y+1表示两个连续的奇数,你能写出表示所有数组规律的函数表达式吗?
依题意,得 6x=4y
即
你能确定自变量的取值范围吗?
∵x,y都是整数
只有当x取偶数时,y才能为整数
∴x取偶数
(x为偶数)
无数组
归纳总结
1. 当用函数表达式表示函数关系式时,在自变量的取值范围内任取一个值,即可确定相应的函数值,同样也可由函数值确定相应的自变量的值,方便为我们解决实际问题.因此有时解决函数问题时,要先确定函数表达式.
2. 在实际问题中确定自变量的取值范围,主要考虑两个因素:
⑴自变量自身表示的意义.如时间、耗油量等不能为负数;
⑵问题中的限制条件.此时多用不等式或不等式组来确定自变量的取值范围.
做一做
一支20 cm长的蜡烛,点燃后,每小时燃烧5 cm.在下图中,哪幅图像能大致刻画出这支蜡烛点燃后剩下的长度h(cm)与点燃时间t(h)之间的函数关系?请说明理由.
关键是清楚图像中横、纵坐标表示的意义
知识点
图像法的初步运用
3
2.分析已知(看已知的是自变量的值还是函数值),通过做x轴或y轴的垂线,在图像上找到对应的点,由点的横坐标或者纵坐标的值读出要求的值.
1.理解横、纵坐标分别表示的实际意义.
3.利用数形结合的思想:将“数”转化为“形” ,由“形”定“数”.
思考:如何获取并运用函数图像的信息?
例题讲解
例 1一水库的水位在最近5 h 内持续上涨,下表记录了这5 h 内6 个时间点的水位高度,其中 t 表示时间,y表示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,
这些点是否在一条直线上?由此你发现水位变化有什么规律?
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
解:可以看出,这6个点 ,且每小时水位 .
由此猜想,在这个时间段中水位可能是以同一速度均匀上升的.
在同一直线上
上升0.3m
x/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
5
(2)水位高度 y 是否为时间 t 的函数?如果是,试写出一个符合表中数据的函数解析式,并画出函数图像.这个函数能表示水位的变化规律吗?
由于水位在最近5小时内持续上涨,对于时间t的每一个确定的值,水位高度y 都有 的值与其对应,所以,y t 的函数.
函数解析式为: .
自变量的取值范围是: . 它表示在这 小时内,水位匀速上升的速度为 ,这个函数可以近似地表示水位的变化规律.
唯一
是
y=0.3t+3
0≤t≤5
5
0.3m/h
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将达到多少m.
如果水位的变化规律不变,按上述函数预测,再持续2小时,水位的高度: .
此时函数图像(线段AB)向 延伸到对应的位置,这时水位高度约为 m.
5.1m
右
5.1
变式练习
一个等腰三角形的周长为12cm,设底边长为ycm ,腰长为xcm.
(1)写出y与x的函数关系式,并指出自变量x的取值范围.
解:由题意得,2x+y=12
∴y=12-2x
∵x+x>y,x+y>x
∴ x+x>12-2x
12-2x>0
解得 3∴y=12-2x( 3x
x
y
(2)画出这个函数的图像.
3
1
4
2
5
-6
-3
O
1
2
3
4
5
-1
x
y
x 3 4 5 6
y 6 4 2 0
6
6
随堂演练
1.一种树苗的高度用h表示,树苗生长的年数用k表示,测得的有关数据如下表(树苗原高为50 cm):
则用年数k表示高度h的关系式是( )
A.h=50k+5 B.h=50+5(k-1)
C.h=50+5k D.h=50(k-1)+5
年数k 1 2 3 4 …
高度h/cm 50+5 50+10 50+15 50+20 …
C
2.汽车开始行驶时,油箱中有油30升,若汽车每小时耗油5升,则表示油箱内的剩油量Q(升)与行驶时间t(时)之间的关系正确的是图中的( )
B
3. 一名老师带领x名学生到动物园参观.已知成人票每张30元,学生票每张10元.设购买门票的总费用为y元,则y与x之间的函数关系式为( )
A.y=10x+30 B.y=40x
C.y=10+30x D. y=20x
A
4. 某研究表明,人在运动时的心跳速度通常与人的年龄有关,下表是测得的一个人在运动时所能承受的每分钟心跳的最高次数b(次)随这个人的年龄a(岁)变化的规律:
年龄a(岁) 1 2 3 4 5
运动时所能承受的每分钟心跳的最高次数b(次) 175 174.2 173.4 172.6 171.8
(1)试写出b与自变量a之间的函数关系式 (不必写出自变量的取值范围);
(2)正常情况下,在运动时,一个12岁的少年能承受的每分钟心跳的最高次数是 次;
(3)若一个50岁的人在运动时,每分钟心跳的次数为148次,则他的状况为 (请填“可能有危险”或“没有危险”).
b=175.8-0.8a
166.2
可能有危险
课堂小结
函数的初步应用
确定实际问题中函数关系式并解决实际问题
分析实际问题中的函数图像并解决问题
第二十章 函数
20.4 函数的初步应用
知识回顾
1.函数概念包含:
(1)两个变量;
(2)两个变量之间的对应关系.
2.函数关系三种表示方法:
(1)表格法
(2)图像法
(3)表达式法
情景导入
摄氏温度和华氏温度都是计量温度单位的,世界上多数国家使用的是摄氏温度,但也有一些国家使用华氏温度.
摄氏温度和华氏温度如何互相转化呢?
获取新知
常用的温度计量标准有两种,一种是摄氏温度(℃),另一种是华氏温度(℉).
想一想:华氏温度与摄氏温度是否具有函数关系呢?
从温度计来看是一个对应一个,那么你能确定它们之间的表达式吗?
知识点
表格法的初步运用
1
一起探究
已知摄氏温度值和华氏温度值有下表所示的对应关系:
摄氏温度/ C 0 10 20 30 40 50
华氏温度/ F 32 50 68 86 104 122
(1)当摄氏温度为30时,华氏温度为多少?
86
摄氏温度/ C 0 10 20 30 40 50
华氏温度/ F 32 50 68 86 104 122
(2)当摄氏温度为36时,由数值表能直接看出华氏温度吗?试写出这两种温度计量之间关系的函数表达式,并求摄氏温度为36时的华氏温度;
观察表格中数据,你发现了什么规律吗?
解:不能由表格直接得出摄氏温度为36时对应的华氏温度.
【分析】观察表格可得,摄氏温度为0°C时,华氏温度为32°F.摄氏温度每增加10°C.华氏温度增加18°F,即摄氏温度增加1°C,华氏温度增加1.8°F.所以,华氏温度=32+1.8×摄氏温度.
若设摄氏温度为t C,华氏温度为f F,则f =1.8t+32.
当t=36时,f=1.8×36+32=96.8.
摄氏温度/ C 0 10 20 30 40 50
华氏温度/ F 32 50 68 86 104 122
(3)当华氏温度为140时,摄氏温度为多少?
【分析】当华氏温度为140时,140=32+1.8×摄氏温度,解方程即可.
解:当f=36时,140=1.8t+32,解得t=60.
得到函数表达式后,任给一个变量值,可确定另一个变量的值.
试着做做
大家都熟悉奥运会的标志图案——五环图,在上面三个环中填入三个连续的偶数,在下面的两个环中填入两个连续的奇数,使得这三个连续偶数的和等于这两个连续奇数的和(如图中已经填好的2,4,6和5,7),请你按照要求再填写两组数.
2
4
6
5
7
知识点
表达式法的初步运用
2
大家谈谈
(1)请和同学交流,各自填写的数组是什么,满足要求的数组有很多吗?
6+8+10=11+13; 10+12+14=17+19; 14+16+18=23+25; 18+20+22=29+31; ……
(2)如果用2x-2,2x,2x+2表示三个连续的偶数,用2y-1,2y+1表示两个连续的奇数,你能写出表示所有数组规律的函数表达式吗?
依题意,得 6x=4y
即
你能确定自变量的取值范围吗?
∵x,y都是整数
只有当x取偶数时,y才能为整数
∴x取偶数
(x为偶数)
无数组
归纳总结
1. 当用函数表达式表示函数关系式时,在自变量的取值范围内任取一个值,即可确定相应的函数值,同样也可由函数值确定相应的自变量的值,方便为我们解决实际问题.因此有时解决函数问题时,要先确定函数表达式.
2. 在实际问题中确定自变量的取值范围,主要考虑两个因素:
⑴自变量自身表示的意义.如时间、耗油量等不能为负数;
⑵问题中的限制条件.此时多用不等式或不等式组来确定自变量的取值范围.
做一做
一支20 cm长的蜡烛,点燃后,每小时燃烧5 cm.在下图中,哪幅图像能大致刻画出这支蜡烛点燃后剩下的长度h(cm)与点燃时间t(h)之间的函数关系?请说明理由.
关键是清楚图像中横、纵坐标表示的意义
知识点
图像法的初步运用
3
2.分析已知(看已知的是自变量的值还是函数值),通过做x轴或y轴的垂线,在图像上找到对应的点,由点的横坐标或者纵坐标的值读出要求的值.
1.理解横、纵坐标分别表示的实际意义.
3.利用数形结合的思想:将“数”转化为“形” ,由“形”定“数”.
思考:如何获取并运用函数图像的信息?
例题讲解
例 1一水库的水位在最近5 h 内持续上涨,下表记录了这5 h 内6 个时间点的水位高度,其中 t 表示时间,y表示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,
这些点是否在一条直线上?由此你发现水位变化有什么规律?
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
解:可以看出,这6个点 ,且每小时水位 .
由此猜想,在这个时间段中水位可能是以同一速度均匀上升的.
在同一直线上
上升0.3m
x/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
5
(2)水位高度 y 是否为时间 t 的函数?如果是,试写出一个符合表中数据的函数解析式,并画出函数图像.这个函数能表示水位的变化规律吗?
由于水位在最近5小时内持续上涨,对于时间t的每一个确定的值,水位高度y 都有 的值与其对应,所以,y t 的函数.
函数解析式为: .
自变量的取值范围是: . 它表示在这 小时内,水位匀速上升的速度为 ,这个函数可以近似地表示水位的变化规律.
唯一
是
y=0.3t+3
0≤t≤5
5
0.3m/h
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将达到多少m.
如果水位的变化规律不变,按上述函数预测,再持续2小时,水位的高度: .
此时函数图像(线段AB)向 延伸到对应的位置,这时水位高度约为 m.
5.1m
右
5.1
变式练习
一个等腰三角形的周长为12cm,设底边长为ycm ,腰长为xcm.
(1)写出y与x的函数关系式,并指出自变量x的取值范围.
解:由题意得,2x+y=12
∴y=12-2x
∵x+x>y,x+y>x
∴ x+x>12-2x
12-2x>0
解得 3
x
y
(2)画出这个函数的图像.
3
1
4
2
5
-6
-3
O
1
2
3
4
5
-1
x
y
x 3 4 5 6
y 6 4 2 0
6
6
随堂演练
1.一种树苗的高度用h表示,树苗生长的年数用k表示,测得的有关数据如下表(树苗原高为50 cm):
则用年数k表示高度h的关系式是( )
A.h=50k+5 B.h=50+5(k-1)
C.h=50+5k D.h=50(k-1)+5
年数k 1 2 3 4 …
高度h/cm 50+5 50+10 50+15 50+20 …
C
2.汽车开始行驶时,油箱中有油30升,若汽车每小时耗油5升,则表示油箱内的剩油量Q(升)与行驶时间t(时)之间的关系正确的是图中的( )
B
3. 一名老师带领x名学生到动物园参观.已知成人票每张30元,学生票每张10元.设购买门票的总费用为y元,则y与x之间的函数关系式为( )
A.y=10x+30 B.y=40x
C.y=10+30x D. y=20x
A
4. 某研究表明,人在运动时的心跳速度通常与人的年龄有关,下表是测得的一个人在运动时所能承受的每分钟心跳的最高次数b(次)随这个人的年龄a(岁)变化的规律:
年龄a(岁) 1 2 3 4 5
运动时所能承受的每分钟心跳的最高次数b(次) 175 174.2 173.4 172.6 171.8
(1)试写出b与自变量a之间的函数关系式 (不必写出自变量的取值范围);
(2)正常情况下,在运动时,一个12岁的少年能承受的每分钟心跳的最高次数是 次;
(3)若一个50岁的人在运动时,每分钟心跳的次数为148次,则他的状况为 (请填“可能有危险”或“没有危险”).
b=175.8-0.8a
166.2
可能有危险
课堂小结
函数的初步应用
确定实际问题中函数关系式并解决实际问题
分析实际问题中的函数图像并解决问题
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
