冀教版数学八年级下册同步课件:20.2 第2课时 函数自变量的取值范围(共19张PPT)
文档属性
| 名称 | 冀教版数学八年级下册同步课件:20.2 第2课时 函数自变量的取值范围(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 12:53:02 | ||
图片预览





文档简介
(共19张PPT)
第二十章 函数
20.2 第2课时 函数自变量的取值范围
知识回顾
1.什么叫做函数?
一般地,在某个变化过程中,有两个变量x和y.如果给定x的一个值,就能相应地确定y的一个值,那么,就称y是x的函数(或者说y与x具有函数关系).其中,x叫做自变量.
2.函数的表示方式?
数值表,图像、表达式.
情景导入
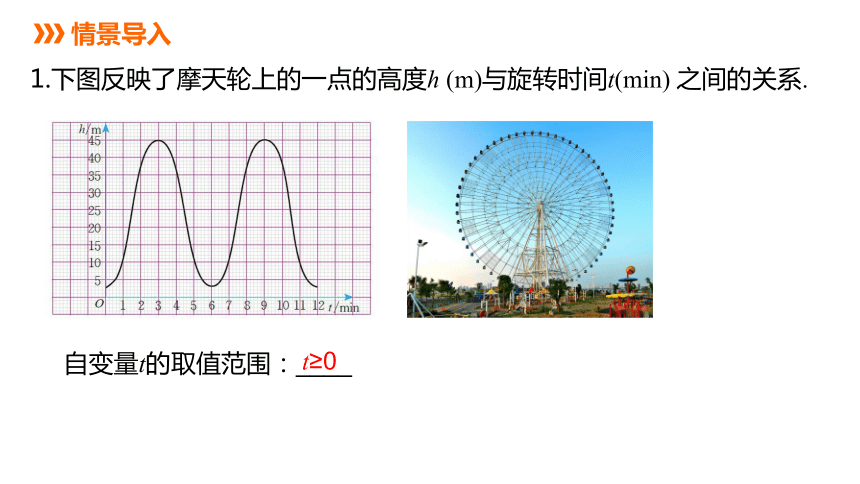
1.下图反映了摩天轮上的一点的高度h (m)与旋转时间t(min) 之间的关系.
自变量t的取值范围:____
t≥0
2.对于给定任一层数n,相应的物体总数y确定吗?
1 2 3 4 5 …
…
1
3
6
10
15
层数 n
物体总数y
自变量n的取值范围:_________
n为正整数
获取新知
知识点
函数表达式中自变量的取值范围
1
下列函数中自变量x的取值范围是什么?
想一想:
当表达式是整式时,自变量可以取任意实数.
∴x取任意实数
当表达式是分式时,要使分母≠0.
∴x≠-2
当表达式是二次根式时,自变量的取值必须使被开方数≥0.
∴x≥5
当表达式是复合式时,自变量的取值是使各式成立的公共解.
∴x≥-2且x≠-1.
做一做
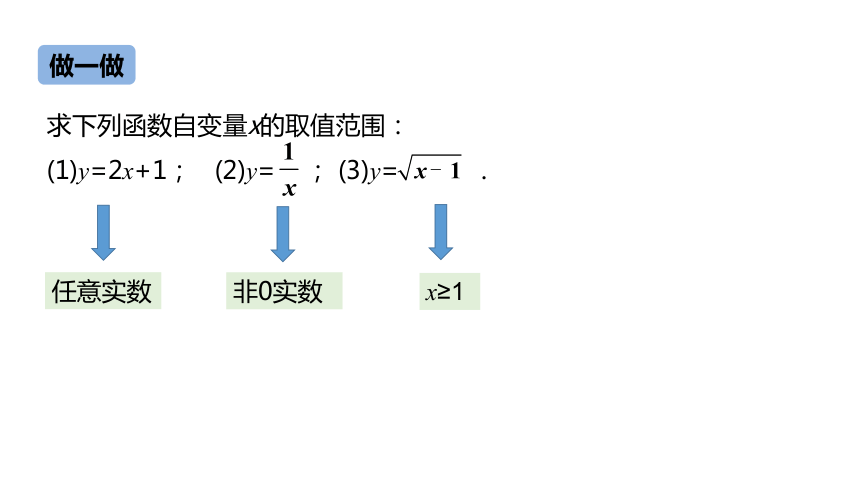
求下列函数自变量x的取值范围:
(1)y=2x+1; (2)y= ; (3)y= .
任意实数
非0实数
x≥1
函数表达式有意义的自变量的取值范围:
4.表达式是复合式时,自变量的取值是使各式成立的公共解.
3.表达式是偶次根式时,自变量的取值必须使被开方数为非负数.表达式是奇次根式时,自变量取全体实数;
1.表达式是整式时,自变量取全体实数;
2.表达式是分式时,自变量的取值要使分母不为0;
归纳总结
大家谈谈
1. 前面讲到的“欣欣报亭1月 6月的每月纯收入S(元)是月份T的函数”.其中自变量T可取哪些值?当T=1.5或T=7时,原问题有意义吗?
2. “某市某一天的气温T(℃)是时刻t的函数”,其中自变量t可取哪些值?如果t取第二天凌晨3时,原问题还有意义吗?
自变量的取值范围是只能取1,2,3,4,5,6中的数.
自变量的取值范围是取0~24中的数.
当T=1.5或T=7时,原问题无意义.
如果t 取第二天凌晨3时,原问题无意义.
知识点
实际问题中自变量的取值范围
2
3. “折纸的层数p是折纸次数n的函数”,其中自变量n可取哪些值?当n=0. 5时,原问题有没有意义?
n只能取正整数.
不同类型的函数问题中,自变量的取值范围可能是不同的,除了受自身的限制外,还要考虑实际问题本身
当n=0. 5时,原问题无意义.
例题讲解
例 如图,等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10 cm,边CA与边MN在同一条直线上,点A与点M重合.让△ABC沿MN方向运动,当点A与点N重合时停止运动.试写出运动中两个图形重叠部分的面积y(cm2)与MA 的长度x(cm)之间的函数关系式,并指出自变量的取值范围.
M(A)
N
P
Q
C
B
┐
┐
C
B
A
思考:①重叠部分的三角形是什么三角形
②怎样表示这个三角形的面积
等腰直角三角形
MA 的一半
M(A)
N
P
Q
C
B
┐
┐
C
B
A
解:因为△ABC是等腰直角三角形,四边形MNPQ是正方形,且AC=BC=QM=MN,所以运动中两个图形的重叠部分也是等腰直角三角形.由MA=x,得y= ,0≤x≤10.
思考:③如何确定x的取值范围
由题意可知,M是定点,A是动点,点A从点M运动到点N,
∴AM最小为0,最大为10.
在实际问题中,函数的自变量不能任意取值,往往是有限制的,在自变量的取值范围内,函数才有实际意义;超出这个范围,函数就没有实际意义了.因此在解决实际问题时,我们要关注自变量的取值范围.
归纳总结
随堂演练
1. 等腰三角形的周长是40 cm,底边长y(cm)是腰长x(cm)的函数,此函数表达式和自变量取值范围正确的是( )
A.y=-2x+40(0<x<20)
B.y=-0.5x+20(10<x<20)
C.y=-2x+40(10<x<20)
D.y=-0.5x+20(0<x<20)
C
2. 若函数 在自变量x=3时无意义,则a= .
-1
3.已知等腰三角形的面积为20 cm2,设它的底边长为x(cm),则底边上的高y(cm)关于x的函数关系式为 ,自变量的取值范围是 .
x>0
4.分别写出下列函数中自变量x的取值范围:
解:(1)自变量x的取值范围是全体实数.
(2)根据题意,得x≠0且x-1≠0,故x≠0,1.
(3)根据题意,得4-x≥0,解得x≤4,
所以自变量x的取值范围是x≤4.
(4)根据题意,得 ,解得x≥5.
5. 已知三角形的三边长分别为10 cm,7 cm,x cm,它的周长为y cm.
(1)求y关于x的函数关系式和自变量x的取值范围;
(2)当x=6时,求三角形的周长;
(3)当x=18时,能求出三角形的周长吗 为什么
解:(1)由题意可得y=x+17.
∵10-7即自变量x的取值范围为3(2)当x=6时,y=17+6=23,
即三角形的周长为23 cm.
(3)不能.理由:∵x=18不在3∴长为10 cm,7 cm,18 cm的三条线段不能构成三角形.
课堂小结
自变量的取值范围
1.使函数表达式有意义
2.符合实际意义
第二十章 函数
20.2 第2课时 函数自变量的取值范围
知识回顾
1.什么叫做函数?
一般地,在某个变化过程中,有两个变量x和y.如果给定x的一个值,就能相应地确定y的一个值,那么,就称y是x的函数(或者说y与x具有函数关系).其中,x叫做自变量.
2.函数的表示方式?
数值表,图像、表达式.
情景导入
1.下图反映了摩天轮上的一点的高度h (m)与旋转时间t(min) 之间的关系.
自变量t的取值范围:____
t≥0
2.对于给定任一层数n,相应的物体总数y确定吗?
1 2 3 4 5 …
…
1
3
6
10
15
层数 n
物体总数y
自变量n的取值范围:_________
n为正整数
获取新知
知识点
函数表达式中自变量的取值范围
1
下列函数中自变量x的取值范围是什么?
想一想:
当表达式是整式时,自变量可以取任意实数.
∴x取任意实数
当表达式是分式时,要使分母≠0.
∴x≠-2
当表达式是二次根式时,自变量的取值必须使被开方数≥0.
∴x≥5
当表达式是复合式时,自变量的取值是使各式成立的公共解.
∴x≥-2且x≠-1.
做一做
求下列函数自变量x的取值范围:
(1)y=2x+1; (2)y= ; (3)y= .
任意实数
非0实数
x≥1
函数表达式有意义的自变量的取值范围:
4.表达式是复合式时,自变量的取值是使各式成立的公共解.
3.表达式是偶次根式时,自变量的取值必须使被开方数为非负数.表达式是奇次根式时,自变量取全体实数;
1.表达式是整式时,自变量取全体实数;
2.表达式是分式时,自变量的取值要使分母不为0;
归纳总结
大家谈谈
1. 前面讲到的“欣欣报亭1月 6月的每月纯收入S(元)是月份T的函数”.其中自变量T可取哪些值?当T=1.5或T=7时,原问题有意义吗?
2. “某市某一天的气温T(℃)是时刻t的函数”,其中自变量t可取哪些值?如果t取第二天凌晨3时,原问题还有意义吗?
自变量的取值范围是只能取1,2,3,4,5,6中的数.
自变量的取值范围是取0~24中的数.
当T=1.5或T=7时,原问题无意义.
如果t 取第二天凌晨3时,原问题无意义.
知识点
实际问题中自变量的取值范围
2
3. “折纸的层数p是折纸次数n的函数”,其中自变量n可取哪些值?当n=0. 5时,原问题有没有意义?
n只能取正整数.
不同类型的函数问题中,自变量的取值范围可能是不同的,除了受自身的限制外,还要考虑实际问题本身
当n=0. 5时,原问题无意义.
例题讲解
例 如图,等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10 cm,边CA与边MN在同一条直线上,点A与点M重合.让△ABC沿MN方向运动,当点A与点N重合时停止运动.试写出运动中两个图形重叠部分的面积y(cm2)与MA 的长度x(cm)之间的函数关系式,并指出自变量的取值范围.
M(A)
N
P
Q
C
B
┐
┐
C
B
A
思考:①重叠部分的三角形是什么三角形
②怎样表示这个三角形的面积
等腰直角三角形
MA 的一半
M(A)
N
P
Q
C
B
┐
┐
C
B
A
解:因为△ABC是等腰直角三角形,四边形MNPQ是正方形,且AC=BC=QM=MN,所以运动中两个图形的重叠部分也是等腰直角三角形.由MA=x,得y= ,0≤x≤10.
思考:③如何确定x的取值范围
由题意可知,M是定点,A是动点,点A从点M运动到点N,
∴AM最小为0,最大为10.
在实际问题中,函数的自变量不能任意取值,往往是有限制的,在自变量的取值范围内,函数才有实际意义;超出这个范围,函数就没有实际意义了.因此在解决实际问题时,我们要关注自变量的取值范围.
归纳总结
随堂演练
1. 等腰三角形的周长是40 cm,底边长y(cm)是腰长x(cm)的函数,此函数表达式和自变量取值范围正确的是( )
A.y=-2x+40(0<x<20)
B.y=-0.5x+20(10<x<20)
C.y=-2x+40(10<x<20)
D.y=-0.5x+20(0<x<20)
C
2. 若函数 在自变量x=3时无意义,则a= .
-1
3.已知等腰三角形的面积为20 cm2,设它的底边长为x(cm),则底边上的高y(cm)关于x的函数关系式为 ,自变量的取值范围是 .
x>0
4.分别写出下列函数中自变量x的取值范围:
解:(1)自变量x的取值范围是全体实数.
(2)根据题意,得x≠0且x-1≠0,故x≠0,1.
(3)根据题意,得4-x≥0,解得x≤4,
所以自变量x的取值范围是x≤4.
(4)根据题意,得 ,解得x≥5.
5. 已知三角形的三边长分别为10 cm,7 cm,x cm,它的周长为y cm.
(1)求y关于x的函数关系式和自变量x的取值范围;
(2)当x=6时,求三角形的周长;
(3)当x=18时,能求出三角形的周长吗 为什么
解:(1)由题意可得y=x+17.
∵10-7
即三角形的周长为23 cm.
(3)不能.理由:∵x=18不在3
课堂小结
自变量的取值范围
1.使函数表达式有意义
2.符合实际意义
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
