冀教版数学八年级下册同步课件:21.3 用待定系数法确定一次函数表达式(共20张PPT)
文档属性
| 名称 | 冀教版数学八年级下册同步课件:21.3 用待定系数法确定一次函数表达式(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 205.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 12:57:43 | ||
图片预览








文档简介
(共20张PPT)
第二十一章 一次函数
21.3 用待定系数法确定一次函数表达式
知识回顾
已知具体的一次函数解析式,如何画出它的图像?
方法:两点法--两点确定一条直线
步骤:列表取值--描点--连线
问题导入
思考:
反过来,已知一个一次函数的图像经过两个具体的点,你能求出它的解析式吗?
获取新知
观察与思考
在图中,直线PQ上两点的坐标分别为P(-20,5),Q(10,20).怎样确定这条直线所对应的一次函数表达式呢?
y
O
x
-5
-10
-15
-20
20
15
10
5
-5
-10
-15
20
15
10
5
知识点
用待定系数法求一次函数的表达式
1
P
Q
分析:因为一次函数的一般形式是y=kx+b(k,b为常数,且k≠0),要求出一次函数的表达式,关键是要确定k和b的值(即待定系数).
阅读下面小惠对此问题的解答过程,并验证小惠求得的一次函数表达式是否正确.
小惠的解答过程如下:
设这个一次函数表达式为y=kx+b.
因为P,Q为直线上的两点,所以这两个点的坐标都满
足表达式y=kx+b ,即
解这个关于k和b的二元一次方程组,得
所以,这个一次函数表达式为
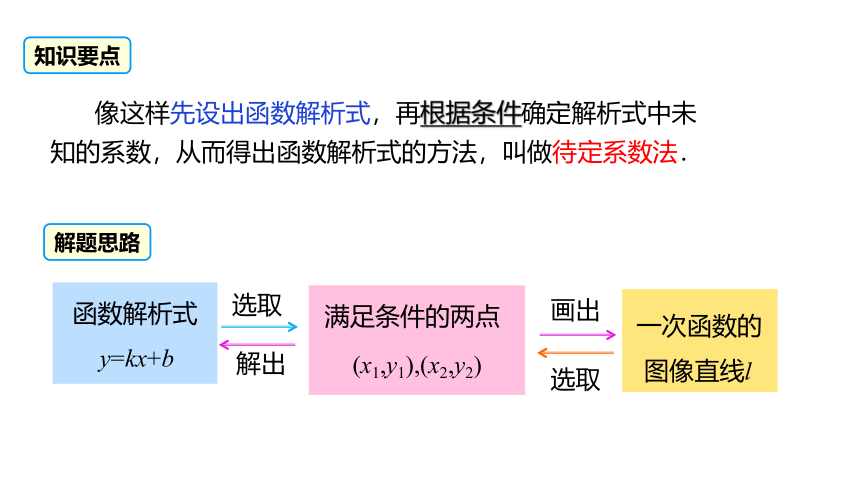
像这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法.
函数解析式
y=kx+b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的
图像直线l
选取
解出
画出
选取
知识要点
解题思路
例1 已知一次函数y=kx+b,当x=1时,y=1;当x=2时,y=3.求这个一次函数的表达式.
∴ k+b=1
2k+b=3
解得 k=2
b=-1
∴这个一次函数的表达式为y=2x-1
解:∵当x=1时,y=1;当x=2时,y=3.
例题讲解
练一练
已知一次函数的图像过点(3,5)与(-4,-9),求这个一次函数的表达式.
解:设这个一次函数的表达式为y=kx+b.
3k+b=5,
-4k+b=-9,
∴这个一次函数的表达式为
解方程组得
把点(3,5)与(-4,-9)分别代入,得:
k=2,
b=-1.
y=2x-1.
总结归纳
(1)设:设一次函数的一般形式 ;
(2)列:把图像上的点 , 代入一次函数的解析式,组成_________方程组;
(3)解:解二元一次方程组得k,b;
(4)还原:把k,b的值代入一次函数的解析式.
y=kx+b(k≠0)
二元一次
待定系数法求一次函数解析式的步骤:
(x1,y1)
(x2,y2)
例2 一辆汽车匀速行驶,当行驶了20 km时,油箱剩余58.4 L油;当行驶了50 km时,油箱剩余56 L油.如果油箱中剩余油y(L)与汽车行驶的路程x(km)之间是一次函数关系,请求出这个一次函数的表达式, 并写出自变量x的取值范围以及常数项的意义.
解:设所求一次函数的表达式为y=kx+b. 根据题意,把已知的两组对应值(20,58. 4)和(50,56)代入 y=kx+b,
得 解得
这个一次函数表达式为y=-0.08x+60.
因为剩余油量y≥0,所以-0.08x+60 ≥0.解得x≤750.
因为路程x≥0,所以0≤x≤750.
因为当x=0时,y=60,所以这辆汽车行驶前油箱存油60 L.
变式练习 某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h)之间为一次函数关系,函数图象如图所示.
(1)求y关于x的函数表达式;
(2)一箱油可供拖拉机工作几小时?
解:(1)由图像可知,函数经过点P(2,30)和点Q(6,10)
设函数表达式为y=kx+b.把已知的两组对应值(2,30)和(6,10)代入,得 ,解得
y关于x的函数表达式为y=-5x+40
(2)由图像可知,一台拖拉机能工作的最长时间是直到剩油为0,
所以当y=0时,即-5x+40=0,解得x=8
答:一箱油可供一台拖拉机工作8小时
根据图象确定一次函数的表达式的方法:从图象上选取两个已知点的坐标,然后运用待定系数法将两点的横、纵坐标代入所设表达式中求出待定系数,从而求出函数的表达式.
归纳总结
随堂演练
1.已知点(4,2)在函数y=2x+b的图像上,则b等于( )
A.6 B.8 C.-6 D.-8
C
2. 如图,直线l是一次函数y=kx+b的图像,填空:
(1)b=______,k=______;
(2)当x=30时,y=______;
(3)当y=30时,x=______.
2
-18
-42
3.已知一次函数的图像经过点(9,0)和点(24,20),写出函数解析式.
解:设一次函数解析式为y=kx+b.
则 解得
所以一次函数解析式为y= x-12.
4. 一辆汽车行驶时的耗油量为0.1升/千米,下图是油箱剩余油量y(升)关于加满油后已行驶的路程x(千米)的函数图像.
(1)根据图像,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量.
(2)求y关于x的函数表达式,并计算该汽车在剩余油量为5升时已行驶的路程.
解:(1)汽车行驶400千米时,油箱内剩余油量为30升.
∵汽车行驶时的耗油量为0.1升/千米,
∴汽车行驶400千米时,耗油量为0.1×400=40(升),
∴加满油时,油箱的油量为30+40=70(升).
(2)设y=kx+b(k≠0),把点(0,70),(400,30)的坐标分别代入,得 ,解得
∴y关于x的函数表达式为y=-0.1x+70.
当y=5时,x=650,
即该汽车在剩余油量为5升时已行驶的路程为650千米.
课堂小结
用待定系数法求一次函数的解析式
2. 代:根据已知条件列出关于k,b的方程(组);
1.设: 设所求的一次函数解析式为y=kx+b;
3.解: 解方程,求出k,b;
4. 写:把求出的k,b代回解析式即可.
第二十一章 一次函数
21.3 用待定系数法确定一次函数表达式
知识回顾
已知具体的一次函数解析式,如何画出它的图像?
方法:两点法--两点确定一条直线
步骤:列表取值--描点--连线
问题导入
思考:
反过来,已知一个一次函数的图像经过两个具体的点,你能求出它的解析式吗?
获取新知
观察与思考
在图中,直线PQ上两点的坐标分别为P(-20,5),Q(10,20).怎样确定这条直线所对应的一次函数表达式呢?
y
O
x
-5
-10
-15
-20
20
15
10
5
-5
-10
-15
20
15
10
5
知识点
用待定系数法求一次函数的表达式
1
P
Q
分析:因为一次函数的一般形式是y=kx+b(k,b为常数,且k≠0),要求出一次函数的表达式,关键是要确定k和b的值(即待定系数).
阅读下面小惠对此问题的解答过程,并验证小惠求得的一次函数表达式是否正确.
小惠的解答过程如下:
设这个一次函数表达式为y=kx+b.
因为P,Q为直线上的两点,所以这两个点的坐标都满
足表达式y=kx+b ,即
解这个关于k和b的二元一次方程组,得
所以,这个一次函数表达式为
像这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法.
函数解析式
y=kx+b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的
图像直线l
选取
解出
画出
选取
知识要点
解题思路
例1 已知一次函数y=kx+b,当x=1时,y=1;当x=2时,y=3.求这个一次函数的表达式.
∴ k+b=1
2k+b=3
解得 k=2
b=-1
∴这个一次函数的表达式为y=2x-1
解:∵当x=1时,y=1;当x=2时,y=3.
例题讲解
练一练
已知一次函数的图像过点(3,5)与(-4,-9),求这个一次函数的表达式.
解:设这个一次函数的表达式为y=kx+b.
3k+b=5,
-4k+b=-9,
∴这个一次函数的表达式为
解方程组得
把点(3,5)与(-4,-9)分别代入,得:
k=2,
b=-1.
y=2x-1.
总结归纳
(1)设:设一次函数的一般形式 ;
(2)列:把图像上的点 , 代入一次函数的解析式,组成_________方程组;
(3)解:解二元一次方程组得k,b;
(4)还原:把k,b的值代入一次函数的解析式.
y=kx+b(k≠0)
二元一次
待定系数法求一次函数解析式的步骤:
(x1,y1)
(x2,y2)
例2 一辆汽车匀速行驶,当行驶了20 km时,油箱剩余58.4 L油;当行驶了50 km时,油箱剩余56 L油.如果油箱中剩余油y(L)与汽车行驶的路程x(km)之间是一次函数关系,请求出这个一次函数的表达式, 并写出自变量x的取值范围以及常数项的意义.
解:设所求一次函数的表达式为y=kx+b. 根据题意,把已知的两组对应值(20,58. 4)和(50,56)代入 y=kx+b,
得 解得
这个一次函数表达式为y=-0.08x+60.
因为剩余油量y≥0,所以-0.08x+60 ≥0.解得x≤750.
因为路程x≥0,所以0≤x≤750.
因为当x=0时,y=60,所以这辆汽车行驶前油箱存油60 L.
变式练习 某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h)之间为一次函数关系,函数图象如图所示.
(1)求y关于x的函数表达式;
(2)一箱油可供拖拉机工作几小时?
解:(1)由图像可知,函数经过点P(2,30)和点Q(6,10)
设函数表达式为y=kx+b.把已知的两组对应值(2,30)和(6,10)代入,得 ,解得
y关于x的函数表达式为y=-5x+40
(2)由图像可知,一台拖拉机能工作的最长时间是直到剩油为0,
所以当y=0时,即-5x+40=0,解得x=8
答:一箱油可供一台拖拉机工作8小时
根据图象确定一次函数的表达式的方法:从图象上选取两个已知点的坐标,然后运用待定系数法将两点的横、纵坐标代入所设表达式中求出待定系数,从而求出函数的表达式.
归纳总结
随堂演练
1.已知点(4,2)在函数y=2x+b的图像上,则b等于( )
A.6 B.8 C.-6 D.-8
C
2. 如图,直线l是一次函数y=kx+b的图像,填空:
(1)b=______,k=______;
(2)当x=30时,y=______;
(3)当y=30时,x=______.
2
-18
-42
3.已知一次函数的图像经过点(9,0)和点(24,20),写出函数解析式.
解:设一次函数解析式为y=kx+b.
则 解得
所以一次函数解析式为y= x-12.
4. 一辆汽车行驶时的耗油量为0.1升/千米,下图是油箱剩余油量y(升)关于加满油后已行驶的路程x(千米)的函数图像.
(1)根据图像,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量.
(2)求y关于x的函数表达式,并计算该汽车在剩余油量为5升时已行驶的路程.
解:(1)汽车行驶400千米时,油箱内剩余油量为30升.
∵汽车行驶时的耗油量为0.1升/千米,
∴汽车行驶400千米时,耗油量为0.1×400=40(升),
∴加满油时,油箱的油量为30+40=70(升).
(2)设y=kx+b(k≠0),把点(0,70),(400,30)的坐标分别代入,得 ,解得
∴y关于x的函数表达式为y=-0.1x+70.
当y=5时,x=650,
即该汽车在剩余油量为5升时已行驶的路程为650千米.
课堂小结
用待定系数法求一次函数的解析式
2. 代:根据已知条件列出关于k,b的方程(组);
1.设: 设所求的一次函数解析式为y=kx+b;
3.解: 解方程,求出k,b;
4. 写:把求出的k,b代回解析式即可.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
