冀教版数学八年级下册同步课件:21.1 第1课时 正比例函数(共20张PPT)
文档属性
| 名称 | 冀教版数学八年级下册同步课件:21.1 第1课时 正比例函数(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 13:02:15 | ||
图片预览






文档简介
(共20张PPT)
第二十一章 一次函数
21.1 第1课时 正比例函数
2. 什么是正比例关系
正比例指两种相关联的量,一种量变化,另一种量也随着变化.
如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.
知识回顾
1. 什么叫函数
在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量.
函数有图象、表格、关系式三种表达方式.
情景导入
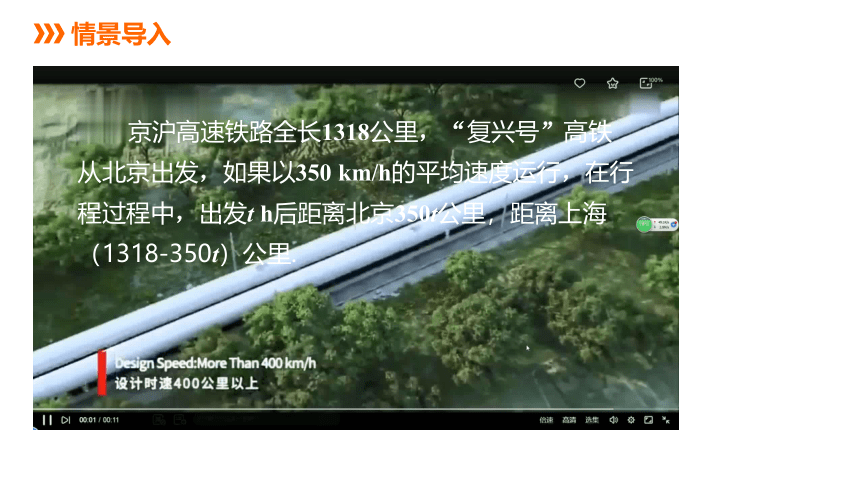
京沪高速铁路全长1318公里,“复兴号”高铁从北京出发,如果以350 km/h的平均速度运行,在行程过程中,出发t h后距离北京350t公里,距离上海(1318-350t)公里.
获取新知
观察与思考
小刚骑自行车去上学,行驶时间和路程的关系如下表:
时间t/min 1 2 3 4 5 … 17.5
路程s/km 0.2 0.4 0.6 0.8 1 … 3.5
知识点
正比例函数的定义
1
(1)小刚行驶的时间和路程成正比例吗?
(2)如果用t(min)表示时间,s(km)表示路程,那么s与t之间的函数关系式具有什么特征呢?
时间t/min 1 2 3 4 5 … 17.5
路程s/km 0.2 0.4 0.6 0.8 1 … 3.5
通过观察,不难发现两个量的比值不变
S与t的比值恒等于0.2,即S=0.2t
2.小米去给学校运动会买奖品,每支铅笔0.5元.若购买铅笔的数量用n(支)表示,花钱的总数用w(元)表示,则用n表示w的函数表达式为_______;
1.小亮每小时读20页书,若读书时间用字母t (h)表示.读过书的页数用字母m(页)表示.则用t 表示m的函数表达式为_______;
3.拧不紧的水龙头每分钟滴100滴水,每滴水约0.05ml,设t min后,水龙头滴水V ml,则用t 表示V的函数表达式为_____;
m=20t
w=0.5n
V=5t
做一做
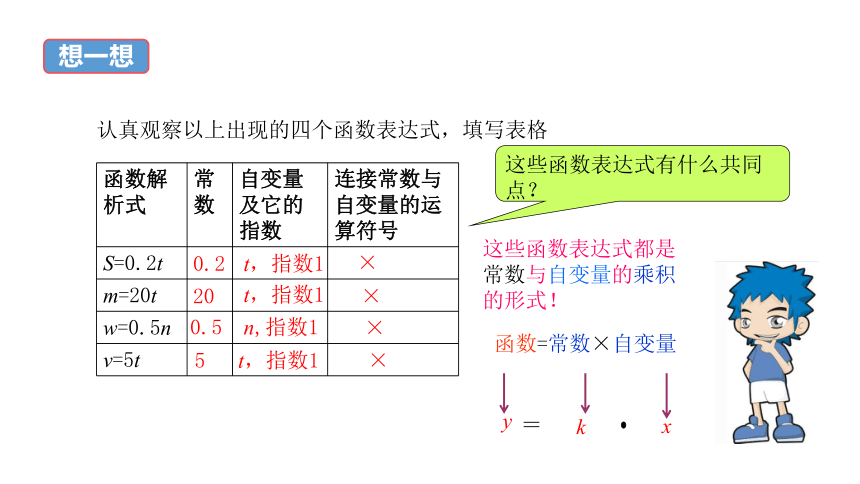
认真观察以上出现的四个函数表达式,填写表格
这些函数表达式都是常数与自变量的乘积的形式!
函数=常数×自变量
y
k
x
=
这些函数表达式有什么共同点?
函数解析式 常数 自变量及它的指数 连接常数与自变量的运算符号
S=0.2t
m=20t
w=0.5n
v=5t
0.2
20
0.5
5
t,指数1
t,指数1
n,指数1
t,指数1
×
×
×
×
想一想
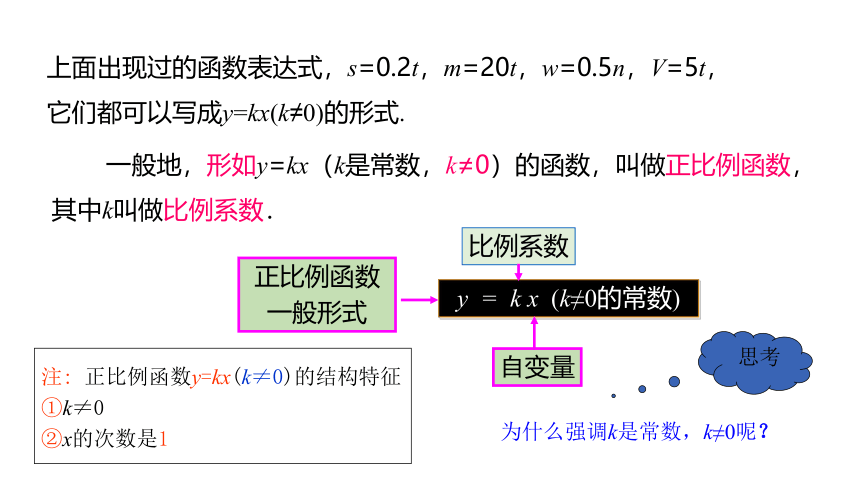
上面出现过的函数表达式,s=0.2t,m=20t,w=0.5n,V=5t,它们都可以写成y=kx(k≠0)的形式.
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
y = k x (k≠0的常数)
比例系数
自变量
正比例函数
一般形式
注: 正比例函数y=kx(k≠0)的结构特征
①k≠0
②x的次数是1
思考
为什么强调k是常数,k≠0呢?
例题讲解
例1 下列函数中,哪些是正比例函数?请指出
其中正比例函数的比例系数.
(1)y=3x; (2)y=2x+1;
(5)y=πx;
解: (1),(3),(5),(6)是正比例函数,比例系数分别
是3, ,π, .
(2)和(4)不是正比例函数.
判断一个函数是否为正比例函数的方法:看两个变量的比是不是常数,即函数是不是形如y=kx(k为常数,且k≠0)的函数.
方法总结
变式练习
1.回答下列问题:
(1)若y=(m-1)x是正比例函数,m取值范围是 ;
(2)当n 时,y=2xn是正比例函数;
(3)当k 时,y=3x+k是正比例函数.
m≠1
=1
=0
已知y与x成正比例,当x=4时,y=8,试求y与x的函数解析式.
解:
∵y与x成正比例
∴y=kx
又∵当x=4时,y=8
∴8=4k
∴k=2
∴y与x的函数解析式为:y=2x
获取新知
知识点
确定正比例函数的表达式
2
求正比例函数解析式的一般步骤
二、把已知的自变量的值和对应的函数值代入所设的解析式,
得到以比例系数k为未知数的方程,解这个方程求出比例系数k;
三、把k的值代入所设的解析式.
一、设所求的正比例函数解析式;
归纳
例2 有一块10公顷的成熟麦田,用一台收割速度为0. 5公顷 /时的小麦收割机来收割.
(1)求收割的面积y(公顷)与收割时间x(h)之间的函数关系式.
(2)求收割完这块麦田需用的时间.
解:(1)y=0.5x.
(2)把y=10代入y=0.5x中,得10=0.5x.
解得x=20,即收割完这块麦田需要20 h.
答:(1) y与x之间的函数关系式为y=0.5x.
(2) 收割完这块麦田需要20 h.
例题讲解
随堂演练
1.下列关系中的两个量成正比例的是( )
A.从甲地到乙地,所用的时间和速度
B.正方形的面积与边长
C.买同样的作业本所要的钱数和作业本的数量
D.人的体重与身高
A
2.下列y关于x的函数中,是正比例函数的为( )
A.y=x2 B.y= C.y= D.y=
C
3. 写出下列问题的函数关系式,并判断哪些是正比例函数:
(1)已知圆的周长C是半径r的函数;
(2)油箱中有油30 L,若油从滑管中均匀流出,150 min流尽,则油箱中余油量Q(L)是流出时间t(min)的函数;
(3)小明以4 km/h的速度匀速前进,则他所走的路程s(km)
是时间t(h)的函数;
(4)某种商品每件进价100元,售出时每件获得20%的利润,销售额y(元)是售出商品数量x(件)的函数.
解:(1)C=2πr,是正比例函数.
(2)Q=30- t,不是正比例函数.
(3)s=4t,是正比例函数.
(4)y=(100+100×20%)x=120x,是正比例函数.
4.已知y与x成正比例,且x=2时, y=-6.
(1)求y与x之间的函数解析式;
(2)求x= 时y的值;
(3)x为何值时,y=9
解:(1)y=-3x.
(2)当x= 时,y=-3×( )=2.
(3)当y=9时,-3x=9,解得x=-3.
课堂小结
正比例函数的概念
形式:y=kx(k≠0)
求正比例函数的解析式
利用正比例函数解决简单的实际问题
1.设
2.代
3.求
4.写
第二十一章 一次函数
21.1 第1课时 正比例函数
2. 什么是正比例关系
正比例指两种相关联的量,一种量变化,另一种量也随着变化.
如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.
知识回顾
1. 什么叫函数
在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量.
函数有图象、表格、关系式三种表达方式.
情景导入
京沪高速铁路全长1318公里,“复兴号”高铁从北京出发,如果以350 km/h的平均速度运行,在行程过程中,出发t h后距离北京350t公里,距离上海(1318-350t)公里.
获取新知
观察与思考
小刚骑自行车去上学,行驶时间和路程的关系如下表:
时间t/min 1 2 3 4 5 … 17.5
路程s/km 0.2 0.4 0.6 0.8 1 … 3.5
知识点
正比例函数的定义
1
(1)小刚行驶的时间和路程成正比例吗?
(2)如果用t(min)表示时间,s(km)表示路程,那么s与t之间的函数关系式具有什么特征呢?
时间t/min 1 2 3 4 5 … 17.5
路程s/km 0.2 0.4 0.6 0.8 1 … 3.5
通过观察,不难发现两个量的比值不变
S与t的比值恒等于0.2,即S=0.2t
2.小米去给学校运动会买奖品,每支铅笔0.5元.若购买铅笔的数量用n(支)表示,花钱的总数用w(元)表示,则用n表示w的函数表达式为_______;
1.小亮每小时读20页书,若读书时间用字母t (h)表示.读过书的页数用字母m(页)表示.则用t 表示m的函数表达式为_______;
3.拧不紧的水龙头每分钟滴100滴水,每滴水约0.05ml,设t min后,水龙头滴水V ml,则用t 表示V的函数表达式为_____;
m=20t
w=0.5n
V=5t
做一做
认真观察以上出现的四个函数表达式,填写表格
这些函数表达式都是常数与自变量的乘积的形式!
函数=常数×自变量
y
k
x
=
这些函数表达式有什么共同点?
函数解析式 常数 自变量及它的指数 连接常数与自变量的运算符号
S=0.2t
m=20t
w=0.5n
v=5t
0.2
20
0.5
5
t,指数1
t,指数1
n,指数1
t,指数1
×
×
×
×
想一想
上面出现过的函数表达式,s=0.2t,m=20t,w=0.5n,V=5t,它们都可以写成y=kx(k≠0)的形式.
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
y = k x (k≠0的常数)
比例系数
自变量
正比例函数
一般形式
注: 正比例函数y=kx(k≠0)的结构特征
①k≠0
②x的次数是1
思考
为什么强调k是常数,k≠0呢?
例题讲解
例1 下列函数中,哪些是正比例函数?请指出
其中正比例函数的比例系数.
(1)y=3x; (2)y=2x+1;
(5)y=πx;
解: (1),(3),(5),(6)是正比例函数,比例系数分别
是3, ,π, .
(2)和(4)不是正比例函数.
判断一个函数是否为正比例函数的方法:看两个变量的比是不是常数,即函数是不是形如y=kx(k为常数,且k≠0)的函数.
方法总结
变式练习
1.回答下列问题:
(1)若y=(m-1)x是正比例函数,m取值范围是 ;
(2)当n 时,y=2xn是正比例函数;
(3)当k 时,y=3x+k是正比例函数.
m≠1
=1
=0
已知y与x成正比例,当x=4时,y=8,试求y与x的函数解析式.
解:
∵y与x成正比例
∴y=kx
又∵当x=4时,y=8
∴8=4k
∴k=2
∴y与x的函数解析式为:y=2x
获取新知
知识点
确定正比例函数的表达式
2
求正比例函数解析式的一般步骤
二、把已知的自变量的值和对应的函数值代入所设的解析式,
得到以比例系数k为未知数的方程,解这个方程求出比例系数k;
三、把k的值代入所设的解析式.
一、设所求的正比例函数解析式;
归纳
例2 有一块10公顷的成熟麦田,用一台收割速度为0. 5公顷 /时的小麦收割机来收割.
(1)求收割的面积y(公顷)与收割时间x(h)之间的函数关系式.
(2)求收割完这块麦田需用的时间.
解:(1)y=0.5x.
(2)把y=10代入y=0.5x中,得10=0.5x.
解得x=20,即收割完这块麦田需要20 h.
答:(1) y与x之间的函数关系式为y=0.5x.
(2) 收割完这块麦田需要20 h.
例题讲解
随堂演练
1.下列关系中的两个量成正比例的是( )
A.从甲地到乙地,所用的时间和速度
B.正方形的面积与边长
C.买同样的作业本所要的钱数和作业本的数量
D.人的体重与身高
A
2.下列y关于x的函数中,是正比例函数的为( )
A.y=x2 B.y= C.y= D.y=
C
3. 写出下列问题的函数关系式,并判断哪些是正比例函数:
(1)已知圆的周长C是半径r的函数;
(2)油箱中有油30 L,若油从滑管中均匀流出,150 min流尽,则油箱中余油量Q(L)是流出时间t(min)的函数;
(3)小明以4 km/h的速度匀速前进,则他所走的路程s(km)
是时间t(h)的函数;
(4)某种商品每件进价100元,售出时每件获得20%的利润,销售额y(元)是售出商品数量x(件)的函数.
解:(1)C=2πr,是正比例函数.
(2)Q=30- t,不是正比例函数.
(3)s=4t,是正比例函数.
(4)y=(100+100×20%)x=120x,是正比例函数.
4.已知y与x成正比例,且x=2时, y=-6.
(1)求y与x之间的函数解析式;
(2)求x= 时y的值;
(3)x为何值时,y=9
解:(1)y=-3x.
(2)当x= 时,y=-3×( )=2.
(3)当y=9时,-3x=9,解得x=-3.
课堂小结
正比例函数的概念
形式:y=kx(k≠0)
求正比例函数的解析式
利用正比例函数解决简单的实际问题
1.设
2.代
3.求
4.写
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
