冀教版数学八年级下册同步课件:22.1 第1课时 平行四边形的概念及边、角的性质(共24张PPT)
文档属性
| 名称 | 冀教版数学八年级下册同步课件:22.1 第1课时 平行四边形的概念及边、角的性质(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 693.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 13:04:24 | ||
图片预览





文档简介
(共24张PPT)
第二十二章 四边形
22.1 第1课时 平行四边形的概念及边、角的性质
知识回顾
问题1 全等三角形的判定方法有哪些?
问题2 什么叫做中心对称图形?
定义法;基本事实:SSS,SAS,ASA;判定定理:AAS.
如果一个图形绕某一个点旋转180°后能与它自身重合,我们就把这个图形叫做中心对称图形,这个点叫做它的对称中心,其中对称的点叫做对应点.
情景导入
观察与思考
教室黑板
瓷砖方案
伸缩门
扶梯
以上四幅图中的图形有什么共同特征?
获取新知
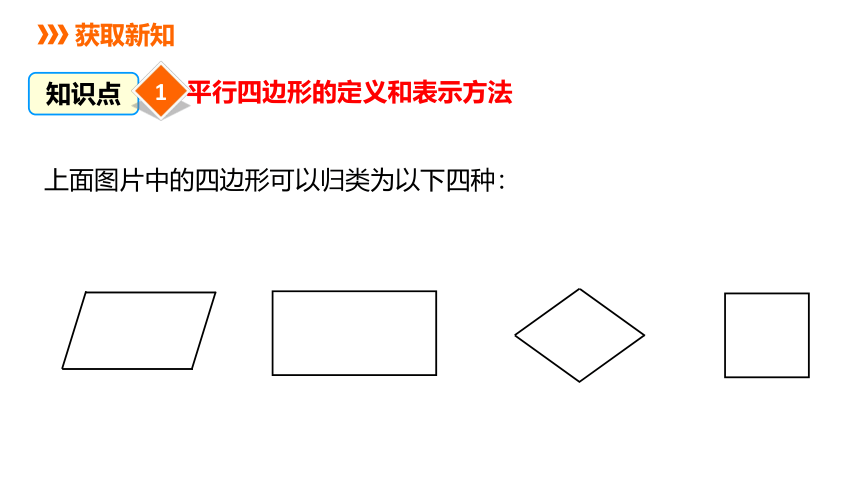
上面图片中的四边形可以归类为以下四种:
知识点
平行四边形的定义和表示方法
1
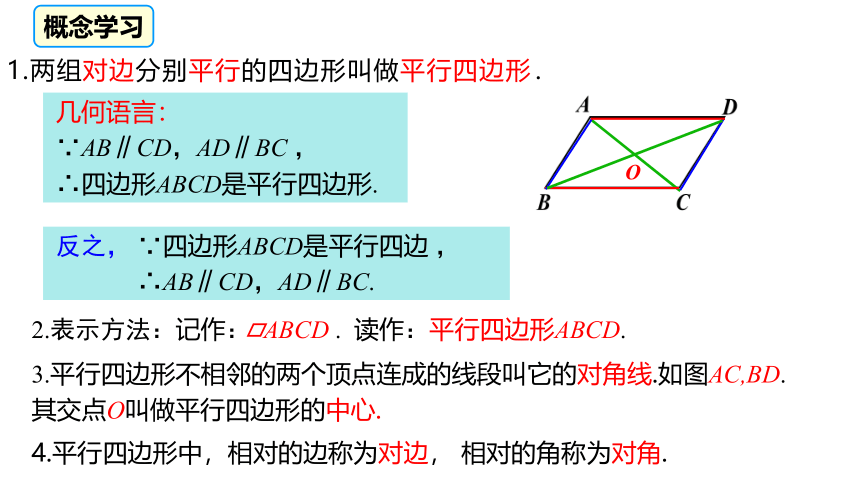
1.两组对边分别平行的四边形叫做平行四边形.
2.表示方法:记作: ABCD . 读作:平行四边形ABCD.
几何语言:
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
3.平行四边形不相邻的两个顶点连成的线段叫它的对角线.如图AC,BD.其交点O叫做平行四边形的中心.
4.平行四边形中,相对的边称为对边, 相对的角称为对角.
O
概念学习
反之, ∵四边形ABCD是平行四边 ,
∴AB∥CD,AD∥BC.
强化概念
平行四边形ABCD
AB∥CD
AC∥BD
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征.
2
3
1
4
5
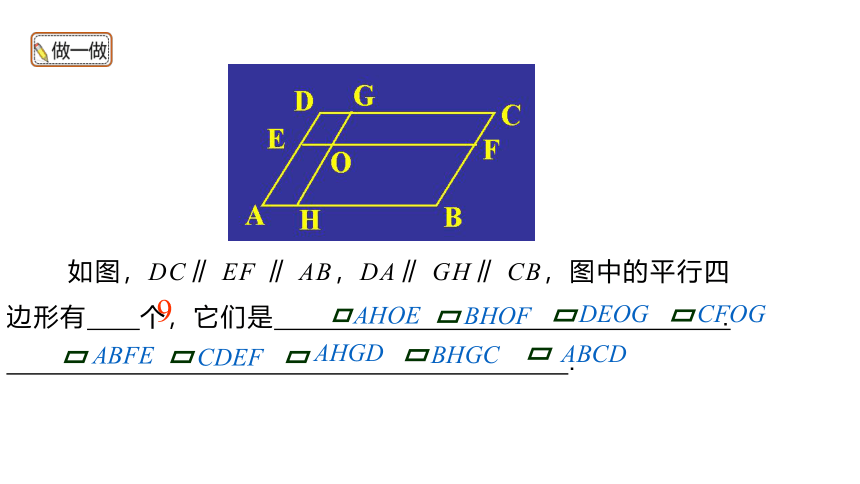
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有 个,它们是 .
.
9
ABCD
BHGC
AHGD
CDEF
ABFE
CFOG
DEOG
BHOF
AHOE
一起探究
1. 如图,在半透明的纸上画一个 ABCD,再复制一个.
将两个图形完全重合,用大头针钉在中心处.使下面的图形不动,将上面的图形绕中心O旋转180°.这两个图形能完全重合 平行四边形是不是中心对称图形?如果是中心对称图形,哪个点是它的对称中心?
被对角线分成的三角形中,关于点O成中心对称的三角形有几对?
知识点
平行四边形的性质
2
A
D
O
C
B
●
D
B
O
C
A
结论:
1.平行四边形是中心对称图形,对角线的交点是它的对称中心;
2.关于O成中心对称的三角形有左与右,上与下两组.
现象:从上述结果看出,□ABCD绕点O旋转180° ,与自身重合.
A
D
O
C
B
●
D
B
O
C
A
2. 在上面的活动过程中,你发现了 ABCD的
对边AD与CB,AB与CD之间具有怎样的数量关系?
对角∠BAD与∠DCB,∠ABC与∠CDA之间具有怎样的数量关系?
线段OA与OC,OB与OD之间具有怎样的数量关系
相等
A
D
O
C
B
●
D
B
O
C
A
发现
平行四边形是中心对称图形,对称中心是两条对角线的交点.
平行四边形的对边相等,对角相等,对角线互相平分.
已知:如图所示,四边形ABCD是平行四边形.
求证:(1)AD=CB,AB=CD.
(2)∠BAD=∠DCB,∠ABC=∠CDA.
A
B
C
D
证明:连接BD.∵AD∥CB,AB∥CD,
∴∠ABD=∠CDB,∠ADB=∠CBD.
又∵BD=DB,∴△ABD≌△CDB.
∴AD=CB,AB=CD,∠BAD=∠DCB.
∵∠ABD=∠CDB,∠ADB=∠CBD,
∴∠ABD+∠CBD=∠CDB+∠ADB,即∠ABC=∠CDA.
连接AC可以吗?
证明
边的性质:平行四边形对边平行;平行四边形对边相等.
角的性质:平行四边形对角相等;平行四边形邻角互补.
符号语言:如图,
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
AB=CD,AD=BC;
∠A=∠C,∠B=∠D,
∠A+∠B=180°,∠B+∠C=180°,
∠C+∠D=180°,∠A+∠D=180°.
A
B
C
D
例题讲解
例1 已知:如图所示, ABCD的周长为22cm,
△ABD的周长为18 cm,求对角线BD的长.
A
B
C
D
分析:求对角线BD的长,要先利用平行四边形的对边相等的性质,得到AD=BC,AB=DC,然后根据 ABCD的周长和△ABD的周长进行推理.
解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=DC.
由已知条件,得
2(AB+AD)=22,
∴AB+AD=11.
又∵AB+AD+BD=18,
∴BD=18-11=7.
A
B
C
D
例2 如图,在 ABCD中,已知∠B+∠D=260°,
求∠A、∠C的度数.
C
D
A
B
解:在 ABCD中,
∵∠B=∠D,∠B+∠D=260°,
∴∠B=∠D=130°.
又∵AD//CB
∴∠A=180°-∠B=180°-130°=50°.
∴∠C=∠A=50°.
随堂演练
1. 如图, ABCD中,EF∥GH∥BC,MN∥AB,则图中平行四边形的个数是( )
A.13
B.14
C.15
D.18
D
2.在 ABCD中,AD=3 cm,AB=2 cm,则 ABCD的周长是 ( )
A.10 cm B.6 cm C.5 cm D.4 cm
A
3. 如图,在 ABCD中,M是BC延长线上的一点,
若∠A=135°,则∠MCD的度数是( )
A.45°
B.55°
C.65°
D.75°
A
4. 在□ABCD中.若∠A+ ∠C= 200°,则∠A=_____,∠B=______.
100°
80°
5.用40 cm长的绳子围成一个平行四边形,使其相邻两边的长度比为3∶2,则较长边的长为 cm.
12
6. 如图,在 ABCD中,点E,F分别在边CB,AD的延长线上,且BE=DF,EF分别与AB,CD交于点G,H.
求证:AG=CH.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,AD∥BC,
∴∠E=∠F.
∵BE=DF,∴AF=CE,
∴△AGF≌△CHE(ASA),
∴AG=CH.
课堂小结
平行
四边形
定义
两组对边分别平行的四边形
性质
边:两组对边分别平行,相等
对称性:平行四边形是中心对称图形,对角线的交点就是对称中心
角:两组对角分别相等,邻角互补
第二十二章 四边形
22.1 第1课时 平行四边形的概念及边、角的性质
知识回顾
问题1 全等三角形的判定方法有哪些?
问题2 什么叫做中心对称图形?
定义法;基本事实:SSS,SAS,ASA;判定定理:AAS.
如果一个图形绕某一个点旋转180°后能与它自身重合,我们就把这个图形叫做中心对称图形,这个点叫做它的对称中心,其中对称的点叫做对应点.
情景导入
观察与思考
教室黑板
瓷砖方案
伸缩门
扶梯
以上四幅图中的图形有什么共同特征?
获取新知
上面图片中的四边形可以归类为以下四种:
知识点
平行四边形的定义和表示方法
1
1.两组对边分别平行的四边形叫做平行四边形.
2.表示方法:记作: ABCD . 读作:平行四边形ABCD.
几何语言:
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
3.平行四边形不相邻的两个顶点连成的线段叫它的对角线.如图AC,BD.其交点O叫做平行四边形的中心.
4.平行四边形中,相对的边称为对边, 相对的角称为对角.
O
概念学习
反之, ∵四边形ABCD是平行四边 ,
∴AB∥CD,AD∥BC.
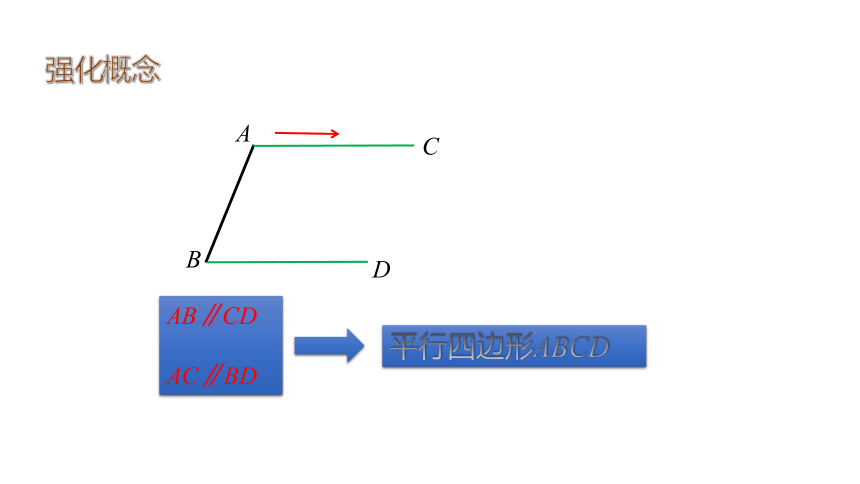
强化概念
平行四边形ABCD
AB∥CD
AC∥BD
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征.
2
3
1
4
5
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有 个,它们是 .
.
9
ABCD
BHGC
AHGD
CDEF
ABFE
CFOG
DEOG
BHOF
AHOE
一起探究
1. 如图,在半透明的纸上画一个 ABCD,再复制一个.
将两个图形完全重合,用大头针钉在中心处.使下面的图形不动,将上面的图形绕中心O旋转180°.这两个图形能完全重合 平行四边形是不是中心对称图形?如果是中心对称图形,哪个点是它的对称中心?
被对角线分成的三角形中,关于点O成中心对称的三角形有几对?
知识点
平行四边形的性质
2
A
D
O
C
B
●
D
B
O
C
A
结论:
1.平行四边形是中心对称图形,对角线的交点是它的对称中心;
2.关于O成中心对称的三角形有左与右,上与下两组.
现象:从上述结果看出,□ABCD绕点O旋转180° ,与自身重合.
A
D
O
C
B
●
D
B
O
C
A
2. 在上面的活动过程中,你发现了 ABCD的
对边AD与CB,AB与CD之间具有怎样的数量关系?
对角∠BAD与∠DCB,∠ABC与∠CDA之间具有怎样的数量关系?
线段OA与OC,OB与OD之间具有怎样的数量关系
相等
A
D
O
C
B
●
D
B
O
C
A
发现
平行四边形是中心对称图形,对称中心是两条对角线的交点.
平行四边形的对边相等,对角相等,对角线互相平分.
已知:如图所示,四边形ABCD是平行四边形.
求证:(1)AD=CB,AB=CD.
(2)∠BAD=∠DCB,∠ABC=∠CDA.
A
B
C
D
证明:连接BD.∵AD∥CB,AB∥CD,
∴∠ABD=∠CDB,∠ADB=∠CBD.
又∵BD=DB,∴△ABD≌△CDB.
∴AD=CB,AB=CD,∠BAD=∠DCB.
∵∠ABD=∠CDB,∠ADB=∠CBD,
∴∠ABD+∠CBD=∠CDB+∠ADB,即∠ABC=∠CDA.
连接AC可以吗?
证明
边的性质:平行四边形对边平行;平行四边形对边相等.
角的性质:平行四边形对角相等;平行四边形邻角互补.
符号语言:如图,
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
AB=CD,AD=BC;
∠A=∠C,∠B=∠D,
∠A+∠B=180°,∠B+∠C=180°,
∠C+∠D=180°,∠A+∠D=180°.
A
B
C
D
例题讲解
例1 已知:如图所示, ABCD的周长为22cm,
△ABD的周长为18 cm,求对角线BD的长.
A
B
C
D
分析:求对角线BD的长,要先利用平行四边形的对边相等的性质,得到AD=BC,AB=DC,然后根据 ABCD的周长和△ABD的周长进行推理.
解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=DC.
由已知条件,得
2(AB+AD)=22,
∴AB+AD=11.
又∵AB+AD+BD=18,
∴BD=18-11=7.
A
B
C
D
例2 如图,在 ABCD中,已知∠B+∠D=260°,
求∠A、∠C的度数.
C
D
A
B
解:在 ABCD中,
∵∠B=∠D,∠B+∠D=260°,
∴∠B=∠D=130°.
又∵AD//CB
∴∠A=180°-∠B=180°-130°=50°.
∴∠C=∠A=50°.
随堂演练
1. 如图, ABCD中,EF∥GH∥BC,MN∥AB,则图中平行四边形的个数是( )
A.13
B.14
C.15
D.18
D
2.在 ABCD中,AD=3 cm,AB=2 cm,则 ABCD的周长是 ( )
A.10 cm B.6 cm C.5 cm D.4 cm
A
3. 如图,在 ABCD中,M是BC延长线上的一点,
若∠A=135°,则∠MCD的度数是( )
A.45°
B.55°
C.65°
D.75°
A
4. 在□ABCD中.若∠A+ ∠C= 200°,则∠A=_____,∠B=______.
100°
80°
5.用40 cm长的绳子围成一个平行四边形,使其相邻两边的长度比为3∶2,则较长边的长为 cm.
12
6. 如图,在 ABCD中,点E,F分别在边CB,AD的延长线上,且BE=DF,EF分别与AB,CD交于点G,H.
求证:AG=CH.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,AD∥BC,
∴∠E=∠F.
∵BE=DF,∴AF=CE,
∴△AGF≌△CHE(ASA),
∴AG=CH.
课堂小结
平行
四边形
定义
两组对边分别平行的四边形
性质
边:两组对边分别平行,相等
对称性:平行四边形是中心对称图形,对角线的交点就是对称中心
角:两组对角分别相等,邻角互补
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
