冀教版数学八年级下册同步课件:22.3 三角形的中位线(共22张PPT)
文档属性
| 名称 | 冀教版数学八年级下册同步课件:22.3 三角形的中位线(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 322.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 13:09:37 | ||
图片预览


文档简介
(共22张PPT)
第二十二章 四边形
22.3 三角形的中位线
知识回顾
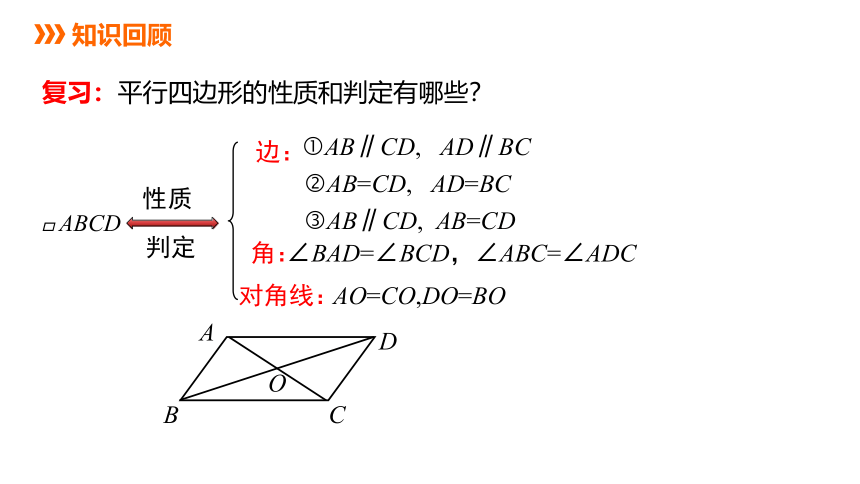
复行四边形的性质和判定有哪些?
边:
角:
对角线:
B
O
D
A
C
AB∥CD, AD∥BC
AB=CD, AD=BC
AB∥CD, AB=CD
∠BAD=∠BCD,∠ABC=∠ADC
AO=CO,DO=BO
判定
性质
情景导入
思考 如图,有一块三角形蛋糕,准备平分给四个小朋友,要求四人所分的形状大小相同,该怎样分呢?
我们探索平行四边形时,常常转化为三角形,利用三角形的全等性质进行研究,今天我们一起来利用平行四边形来探索三角形的某些问题吧!
获取新知
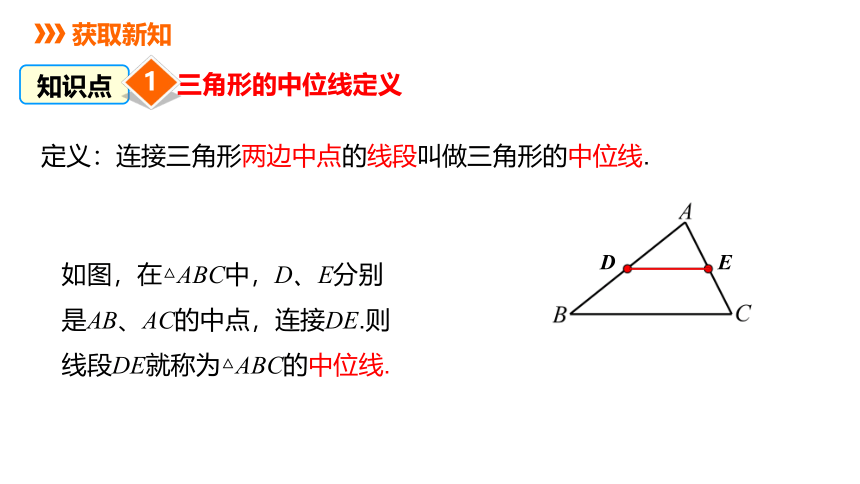
定义:连接三角形两边中点的线段叫做三角形的中位线.
如图,在△ABC中,D、E分别是AB、AC的中点,连接DE.则线段DE就称为△ABC的中位线.
D
E
知识点
三角形的中位线定义
1
一起探究
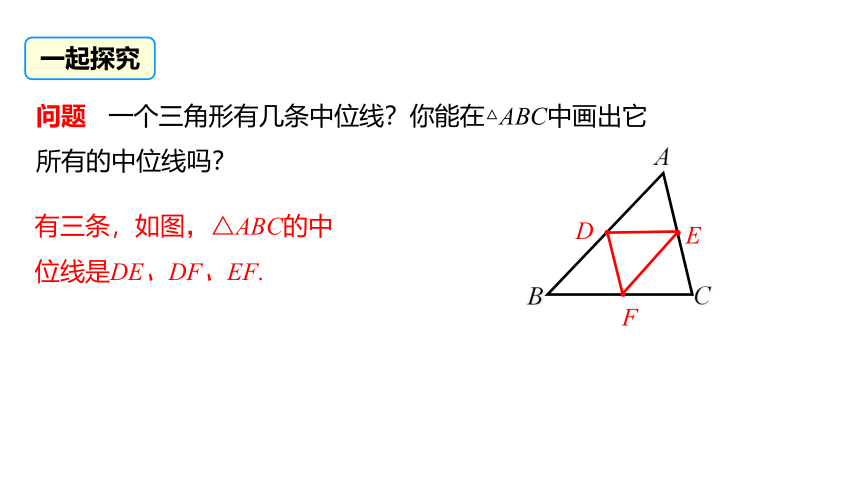
问题 一个三角形有几条中位线?你能在△ABC中画出它所有的中位线吗?
有三条,如图,△ABC的中位线是DE、DF、EF.
A
B
C
D
E
F
延伸思考
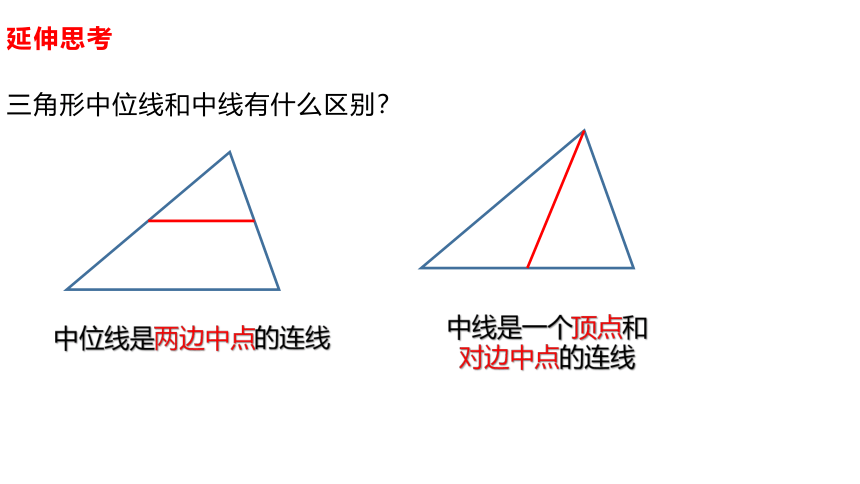
三角形中位线和中线有什么区别?
中位线是两边中点的连线
中线是一个顶点和
对边中点的连线
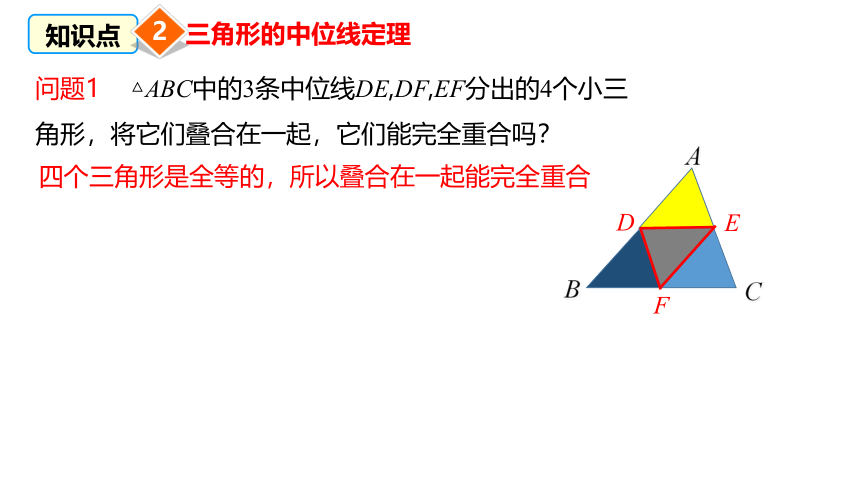
问题1 △ABC中的3条中位线DE,DF,EF分出的4个小三角形,将它们叠合在一起,它们能完全重合吗?
D
E
F
A
B
C
四个三角形是全等的,所以叠合在一起能完全重合
知识点
三角形的中位线定理
2
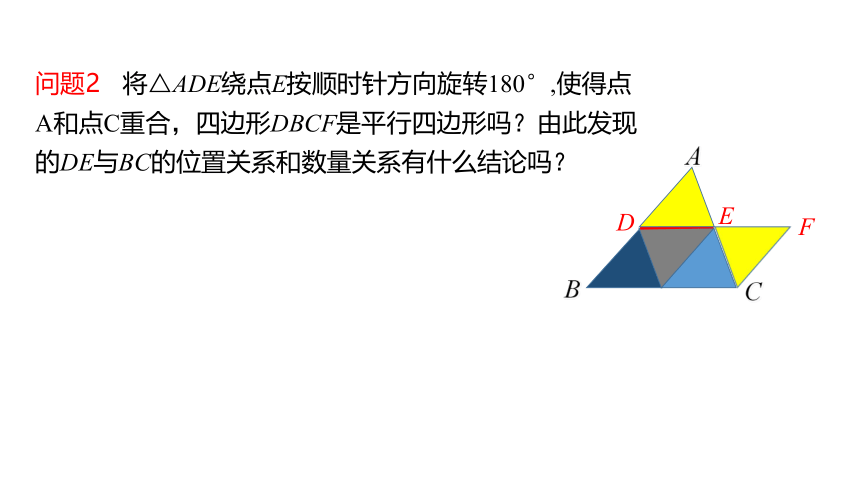
问题2 将△ADE绕点E按顺时针方向旋转180°,使得点A和点C重合,四边形DBCF是平行四边形吗?由此发现的DE与BC的位置关系和数量关系有什么结论吗?
D
A
B
C
E
F
D
E
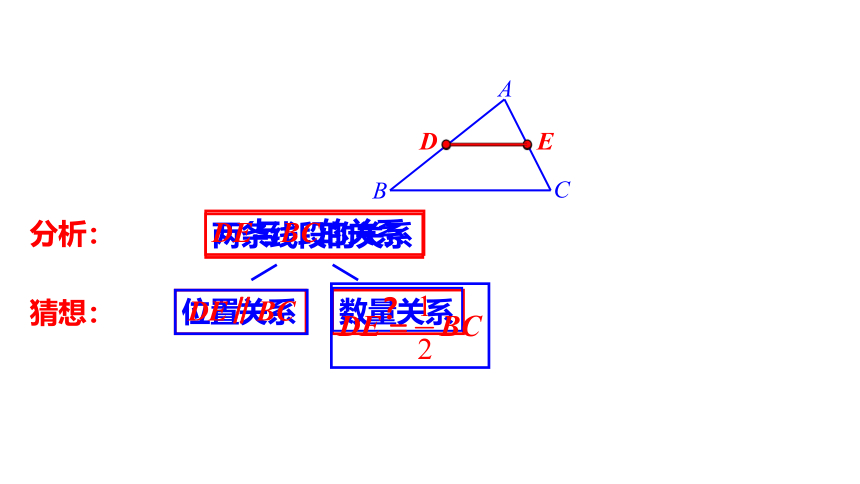
两条线段的关系
位置关系
数量关系
分析:
DE与BC的关系
猜想:
DE∥BC
?
猜想:三角形的中位线平行于第三边,且等于第三边的一半.
已知:如图,D,E分别为△ABC的边AB,AC的中点.
求证:DE∥BC,且DE= BC.
A
B
C
D
E
证明猜想
证明:延长DE到点F,使EF=DE.连接CF.
在△ADE和△CFE中,
∵ AE=CE,∠AED=∠CEF,DE=FE,
∴ △ADE≌△CFE.
∴AD=CF,∠A=∠ECF.∴AD∥CF,即BD∥CF.
又∵BD=AD=CF,
∴四边形DBCF是平行四边形.
∴DE∥BC,且DF=BC.
∴DE= DF= BC.
A
B
C
D
E
F
同学们还有其他添加辅助线的方法吗?
A
B
C
E
D
F
证法二:如图,延长DE至F,
使EF=DE,
连接CD、AF、CF,
∵AE=EC
∴DE=EF
∴四边形ADCF是平行四边形 ∴AD FC
又D为AB中点,
∴DB FC
∴四边形BCFD是平行四边形
∴DE// BC 且DE=EF= BC .
C
E
D
F
B
A
证法三:过点C作AB的平行线交DE的延长线于F,
∵CF∥AB,
∴∠A=∠ECF
又AE=EC,∠AED=∠CEF
∴△ADE≌△CFE
∴ AD=FC
又DB=AD,
∴DB FC
∴四边形BCFD是平行四边形.
∴DE// BC 且DE=EF= BC .
中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
归纳总结
几何语言描述:
∵AD=BD,AE=EC,
∴DE∥BC,且DE= BC.
D
E
位置关系
数量关系
三角形中位线定理是证明两线的平行关系、线段的倍分关系重要理论依据之一.
例题讲解
例1 已知:如图,在三角形ABC中,D,E,F分别为AB,BC,AC的中点,AC=12,BC=16, 求四边形DECF的周长.
解:在△ABC中,
∵D,E分别为AB,BC的中点,
∴DE=FC= AC=6.
同理DF=EC= BC=8.
∴四边形DECF的周长= DE+FC+DF+EC=28.
B
C
F
D
E
A
例题讲解
例1 已知:如图,在四边形ABCD中,AD=BC,P为对角线BD的中点,M为DC的中点,N为AB的中点. 求证:PMN是等腰三角形.
A
B
C
D
M
N
P
证明:在△ABD中,
∵N,P分别为AB,BD的中点,
∴PN= AD.
同理PM= BC.
又∵AD=BC,
∴PN=PM.
∴ △PMN是等腰三角形.
随堂演练
1. 如图所示,在△ABC中,AB=8,AC=10,且AD=4,CE=5,
则下列线段中是△ABC的中位线的是( )
A.线段CD B.线段BE
C.线段DE D.线段AE
C
2.A,B两村相隔一座大山,你能想办法测出A,B两村的直线距离AB的大小吗?若MN=360 m,则AB=_______.
A
B
C
M
N
720 m
3. 如图,顺次连接四边形ABCD四边的中点E,F,G,H,则四边形EFGH的形状一定是 .
平行四边形
4. 如图,在△ABC中,D、E分别为AC、BC的中点,AF平分∠CAB,交DE于点F.若DF=3,求AC的长.
解:∵D、E分别为AC、BC的中点,
∴DE∥AB,
∴∠2=∠3.
又∵AF平分∠CAB,
∴∠1=∠3,
∴∠1=∠2,
∴AD=DF=3,
∴AC=2AD=2DF=6.
1
2
3
5.如图, ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵ ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE= CD,
∴OE= BC,
∴△DOE的周长为OD+OE+DE=
(BD+BC+CD)=15,
即△DOE的周长为15.
三角形的中位线
定义:连接三角形两边中点的线段叫做三角形的中位线.
性质:三角形的中位线平行于第三边,且等于第三边的一半.
课堂小结
第二十二章 四边形
22.3 三角形的中位线
知识回顾
复行四边形的性质和判定有哪些?
边:
角:
对角线:
B
O
D
A
C
AB∥CD, AD∥BC
AB=CD, AD=BC
AB∥CD, AB=CD
∠BAD=∠BCD,∠ABC=∠ADC
AO=CO,DO=BO
判定
性质
情景导入
思考 如图,有一块三角形蛋糕,准备平分给四个小朋友,要求四人所分的形状大小相同,该怎样分呢?
我们探索平行四边形时,常常转化为三角形,利用三角形的全等性质进行研究,今天我们一起来利用平行四边形来探索三角形的某些问题吧!
获取新知
定义:连接三角形两边中点的线段叫做三角形的中位线.
如图,在△ABC中,D、E分别是AB、AC的中点,连接DE.则线段DE就称为△ABC的中位线.
D
E
知识点
三角形的中位线定义
1
一起探究
问题 一个三角形有几条中位线?你能在△ABC中画出它所有的中位线吗?
有三条,如图,△ABC的中位线是DE、DF、EF.
A
B
C
D
E
F
延伸思考
三角形中位线和中线有什么区别?
中位线是两边中点的连线
中线是一个顶点和
对边中点的连线
问题1 △ABC中的3条中位线DE,DF,EF分出的4个小三角形,将它们叠合在一起,它们能完全重合吗?
D
E
F
A
B
C
四个三角形是全等的,所以叠合在一起能完全重合
知识点
三角形的中位线定理
2
问题2 将△ADE绕点E按顺时针方向旋转180°,使得点A和点C重合,四边形DBCF是平行四边形吗?由此发现的DE与BC的位置关系和数量关系有什么结论吗?
D
A
B
C
E
F
D
E
两条线段的关系
位置关系
数量关系
分析:
DE与BC的关系
猜想:
DE∥BC
?
猜想:三角形的中位线平行于第三边,且等于第三边的一半.
已知:如图,D,E分别为△ABC的边AB,AC的中点.
求证:DE∥BC,且DE= BC.
A
B
C
D
E
证明猜想
证明:延长DE到点F,使EF=DE.连接CF.
在△ADE和△CFE中,
∵ AE=CE,∠AED=∠CEF,DE=FE,
∴ △ADE≌△CFE.
∴AD=CF,∠A=∠ECF.∴AD∥CF,即BD∥CF.
又∵BD=AD=CF,
∴四边形DBCF是平行四边形.
∴DE∥BC,且DF=BC.
∴DE= DF= BC.
A
B
C
D
E
F
同学们还有其他添加辅助线的方法吗?
A
B
C
E
D
F
证法二:如图,延长DE至F,
使EF=DE,
连接CD、AF、CF,
∵AE=EC
∴DE=EF
∴四边形ADCF是平行四边形 ∴AD FC
又D为AB中点,
∴DB FC
∴四边形BCFD是平行四边形
∴DE// BC 且DE=EF= BC .
C
E
D
F
B
A
证法三:过点C作AB的平行线交DE的延长线于F,
∵CF∥AB,
∴∠A=∠ECF
又AE=EC,∠AED=∠CEF
∴△ADE≌△CFE
∴ AD=FC
又DB=AD,
∴DB FC
∴四边形BCFD是平行四边形.
∴DE// BC 且DE=EF= BC .
中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
归纳总结
几何语言描述:
∵AD=BD,AE=EC,
∴DE∥BC,且DE= BC.
D
E
位置关系
数量关系
三角形中位线定理是证明两线的平行关系、线段的倍分关系重要理论依据之一.
例题讲解
例1 已知:如图,在三角形ABC中,D,E,F分别为AB,BC,AC的中点,AC=12,BC=16, 求四边形DECF的周长.
解:在△ABC中,
∵D,E分别为AB,BC的中点,
∴DE=FC= AC=6.
同理DF=EC= BC=8.
∴四边形DECF的周长= DE+FC+DF+EC=28.
B
C
F
D
E
A
例题讲解
例1 已知:如图,在四边形ABCD中,AD=BC,P为对角线BD的中点,M为DC的中点,N为AB的中点. 求证:PMN是等腰三角形.
A
B
C
D
M
N
P
证明:在△ABD中,
∵N,P分别为AB,BD的中点,
∴PN= AD.
同理PM= BC.
又∵AD=BC,
∴PN=PM.
∴ △PMN是等腰三角形.
随堂演练
1. 如图所示,在△ABC中,AB=8,AC=10,且AD=4,CE=5,
则下列线段中是△ABC的中位线的是( )
A.线段CD B.线段BE
C.线段DE D.线段AE
C
2.A,B两村相隔一座大山,你能想办法测出A,B两村的直线距离AB的大小吗?若MN=360 m,则AB=_______.
A
B
C
M
N
720 m
3. 如图,顺次连接四边形ABCD四边的中点E,F,G,H,则四边形EFGH的形状一定是 .
平行四边形
4. 如图,在△ABC中,D、E分别为AC、BC的中点,AF平分∠CAB,交DE于点F.若DF=3,求AC的长.
解:∵D、E分别为AC、BC的中点,
∴DE∥AB,
∴∠2=∠3.
又∵AF平分∠CAB,
∴∠1=∠3,
∴∠1=∠2,
∴AD=DF=3,
∴AC=2AD=2DF=6.
1
2
3
5.如图, ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵ ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE= CD,
∴OE= BC,
∴△DOE的周长为OD+OE+DE=
(BD+BC+CD)=15,
即△DOE的周长为15.
三角形的中位线
定义:连接三角形两边中点的线段叫做三角形的中位线.
性质:三角形的中位线平行于第三边,且等于第三边的一半.
课堂小结
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
