冀教版数学八年级下册同步课件:22.4 第2课时 矩形的判定(共20张PPT)
文档属性
| 名称 | 冀教版数学八年级下册同步课件:22.4 第2课时 矩形的判定(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 305.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
第二十二章 四边形
22.4 第2课时 矩形的判定
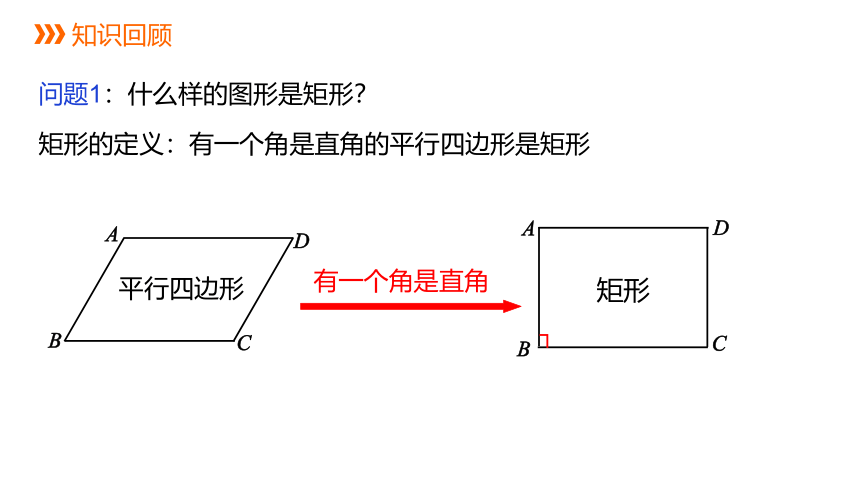
知识回顾
矩形的定义:有一个角是直角的平行四边形是矩形
问题1:什么样的图形是矩形?
有一个角是直角
平行四边形
矩形
┐
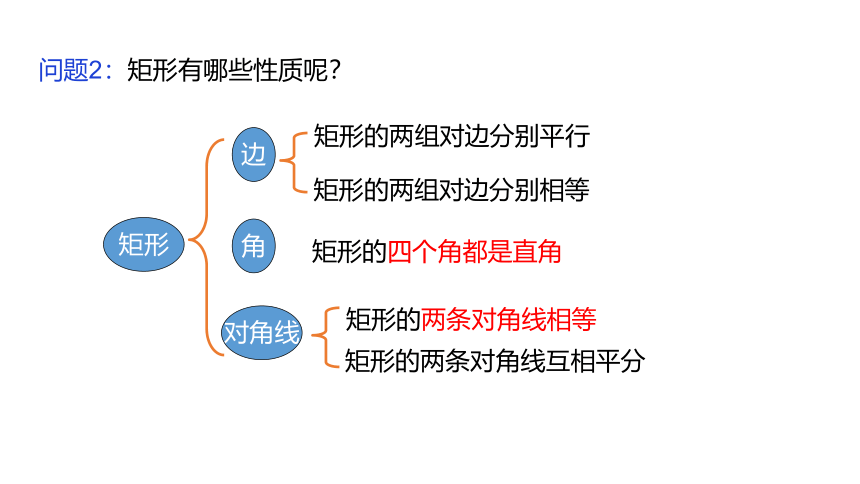
问题2:矩形有哪些性质呢?
矩形的两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形的四个角都是直角
矩形的两条对角线相等
边
对角线
角
矩形
情景导入
思考 工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
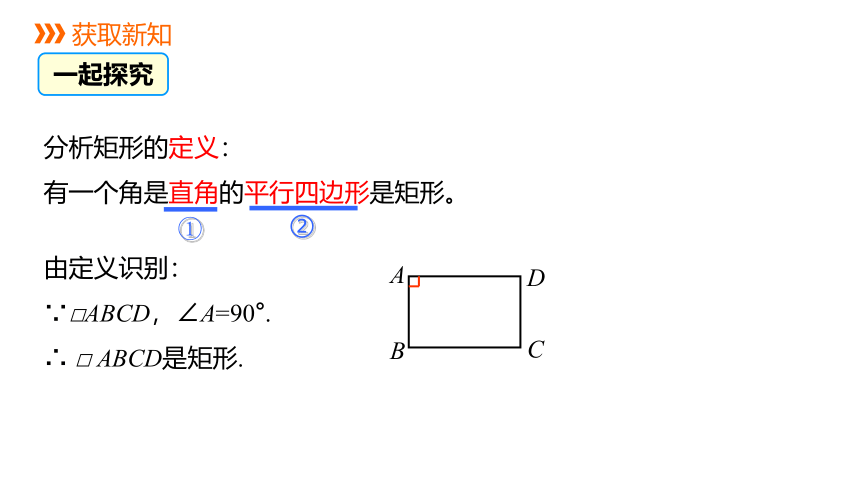
获取新知
一起探究
分析矩形的定义:
有一个角是直角的平行四边形是矩形。
由定义识别:
∵□ABCD,∠A=90°.
∴ □ ABCD是矩形.
①
②
A
B
C
D
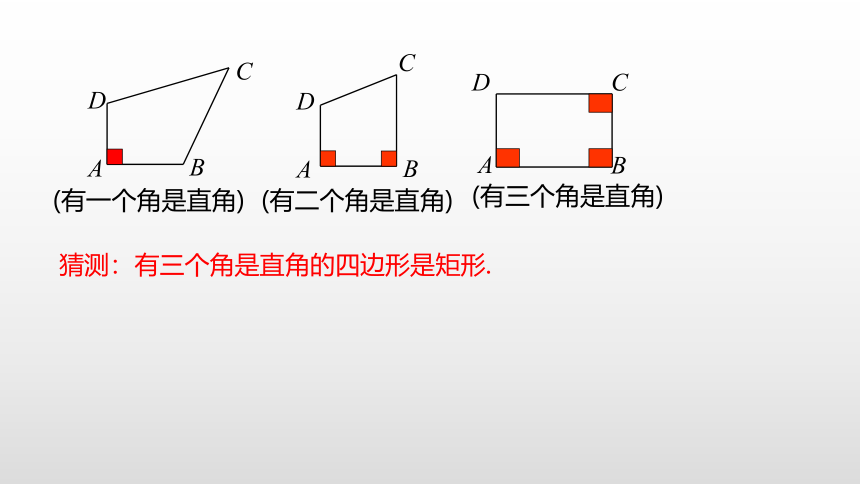
问题1 除了定义以外,矩形的性质的逆命题能否作为矩形判定的方法呢?
性质:矩形的四个角都是直角
逆命题:四个角是直角的四边形是矩形
条件
结论
条件
结论
?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
猜测:有三个角是直角的四边形是矩形.
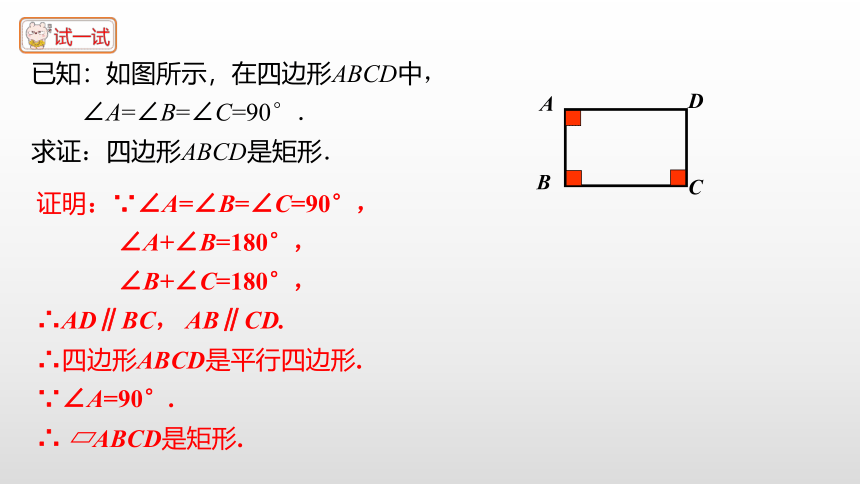
已知:如图所示,在四边形ABCD中,
∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
A
B
C
D
证明:∵∠A=∠B=∠C=90°,
∠A+∠B=180°,
∠B+∠C=180°,
∴AD∥BC, AB∥CD.
∴四边形ABCD是平行四边形.
∵∠A=90°.
∴ ABCD是矩形.
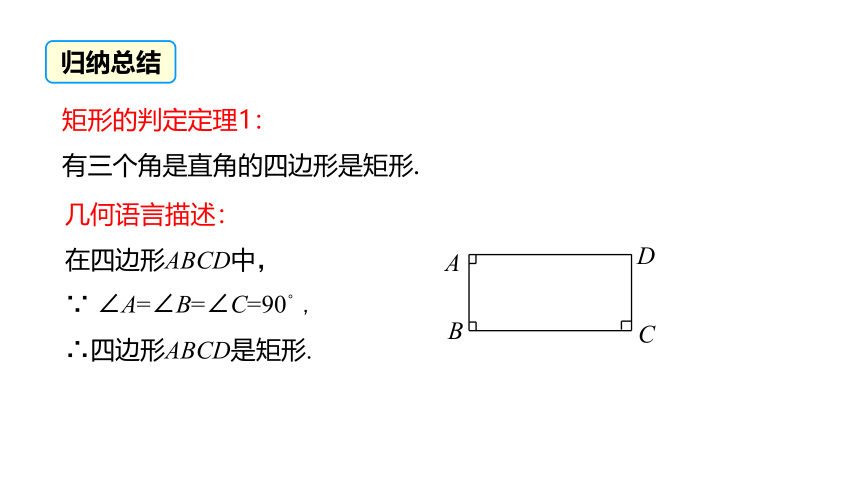
矩形的判定定理1:
有三个角是直角的四边形是矩形.
归纳总结
几何语言描述:
在四边形ABCD中,
∵ ∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
A
B
C
D
例题讲解
例1 如图, ABCD的四个内角的平分线分别相交于点E,F,G,H. 求证:四边形EFGH是矩形.
证明:∵AB∥CD,
∴∠ABC+∠BCD=180°.
∵BG平分∠ABC,CG平分∠BCD,
∴∠GBC+∠GCB= ∠ABC+ ∠BCD= ×180°=90°,
∴∠BGC=90°.
同理可得∠AFB=∠AED=90°.
∴∠GFE=∠FEH=∠FGH=90°.
∴四边形EFGH是矩形.
性质:矩形的对角线相等
逆命题:对角线相等的平行四边形是矩形
条件
结论
条件
结论
?
获取新知
问题2 我们知道矩形的对角线相等,反过来,它的逆命题能否作为矩形判定的方法呢?
已知:在 ABCD,AC=BD.
求证: ABCD是矩形.
证明:∵ 四边形ABCD是平行四边形,
∴AD//BC,AD=BC.
在△ABD和△BAC中,∵ AD=BC,AB=BA,AC=BD,
∴△ABD≌△BAC,∴ ∠DAB=∠CBA.
又∵ AD//BC.
∴ ∠DAB+∠CBA=180°.∴∠DAB=∠CBA= 90°.
∴□ ABCD是矩形.
A
B
C
D
矩形的判定定理2:
对角线相等的平行四边形是矩形.
归纳总结
几何语言描述:
在平行四边形ABCD中,
∵ AC=BD,
∴平行四边形ABCD是矩形.
A
B
C
D
例题讲解
例2 已知:如图,在矩形ABCD中,E,F,G,H 分别为OA,OB,OC,OD的中点. 求证:四边形EFGH是矩形.
B
C
D
E
F
G
H
O
A
证明:∵四边形ABCD是矩形,
∴AC=BD.且 OA=OC,OB=OD.
∴OA=OC=OB=OD.
又∵E,F,G,H 分别为OA,OB,OC,OD 的中点,
∴OE=OG=OF=OH.
∴四边形EFGH是平行四边形.
又∵EG=OE+OG=OF+OH= HF,
∴四边形EFGH是矩形.
随堂演练
1. 如图,要使 ABCD成为矩形,需添加的条件是( )
A.AB=BC
B.AO=BO
C.∠1=∠2
D.AC⊥BD
B
2.如图,在Rt△ABC中,∠BAC=90°,P为边BC上一点,PE⊥AB于E,PF⊥AC于F,AP=4,则EF的值为( )
A.3
B.4
C.2.4
D.2.5
B
3. 如图,木工师傅要做一个矩形木框,做好以后测量得长AB=CD=80 cm,宽AD=BC=60 cm,对角线AC的长为1 m,则这个木框 (填“合格”或“不合格”),判定的依据是 .
合格
有一个角是直角的平行四边形是矩形
4. 如图,在 ABCD中,延长AD到点E,使DE=AD,连接EB,EC,DB,请你添加一个条件______________________,使四边形DBCE是矩形.
EB=DC(答案不唯一)
5. 如图所示,四边形ABCD是平行四边形,点E在CB的延长线上,且BE=BC,DE=DC,连接AE.
求证:四边形AEBD是矩形.
证明: ∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,CD=AB.
∵BC=BE,∴AD=BE.
又AD//BE,∴四边形AEBD是平行四边形.
∵DE=DC,∴AB=DE,
∴平行四边形AEBD是矩形.
课堂小结
矩形的判定方法:
平行四边形
四边形
矩形
对角线
互相平分
有三个角是直角
有一个角是直角
对角线相等
第二十二章 四边形
22.4 第2课时 矩形的判定
知识回顾
矩形的定义:有一个角是直角的平行四边形是矩形
问题1:什么样的图形是矩形?
有一个角是直角
平行四边形
矩形
┐
问题2:矩形有哪些性质呢?
矩形的两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形的四个角都是直角
矩形的两条对角线相等
边
对角线
角
矩形
情景导入
思考 工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
获取新知
一起探究
分析矩形的定义:
有一个角是直角的平行四边形是矩形。
由定义识别:
∵□ABCD,∠A=90°.
∴ □ ABCD是矩形.
①
②
A
B
C
D
问题1 除了定义以外,矩形的性质的逆命题能否作为矩形判定的方法呢?
性质:矩形的四个角都是直角
逆命题:四个角是直角的四边形是矩形
条件
结论
条件
结论
?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
猜测:有三个角是直角的四边形是矩形.
已知:如图所示,在四边形ABCD中,
∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
A
B
C
D
证明:∵∠A=∠B=∠C=90°,
∠A+∠B=180°,
∠B+∠C=180°,
∴AD∥BC, AB∥CD.
∴四边形ABCD是平行四边形.
∵∠A=90°.
∴ ABCD是矩形.
矩形的判定定理1:
有三个角是直角的四边形是矩形.
归纳总结
几何语言描述:
在四边形ABCD中,
∵ ∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
A
B
C
D
例题讲解
例1 如图, ABCD的四个内角的平分线分别相交于点E,F,G,H. 求证:四边形EFGH是矩形.
证明:∵AB∥CD,
∴∠ABC+∠BCD=180°.
∵BG平分∠ABC,CG平分∠BCD,
∴∠GBC+∠GCB= ∠ABC+ ∠BCD= ×180°=90°,
∴∠BGC=90°.
同理可得∠AFB=∠AED=90°.
∴∠GFE=∠FEH=∠FGH=90°.
∴四边形EFGH是矩形.
性质:矩形的对角线相等
逆命题:对角线相等的平行四边形是矩形
条件
结论
条件
结论
?
获取新知
问题2 我们知道矩形的对角线相等,反过来,它的逆命题能否作为矩形判定的方法呢?
已知:在 ABCD,AC=BD.
求证: ABCD是矩形.
证明:∵ 四边形ABCD是平行四边形,
∴AD//BC,AD=BC.
在△ABD和△BAC中,∵ AD=BC,AB=BA,AC=BD,
∴△ABD≌△BAC,∴ ∠DAB=∠CBA.
又∵ AD//BC.
∴ ∠DAB+∠CBA=180°.∴∠DAB=∠CBA= 90°.
∴□ ABCD是矩形.
A
B
C
D
矩形的判定定理2:
对角线相等的平行四边形是矩形.
归纳总结
几何语言描述:
在平行四边形ABCD中,
∵ AC=BD,
∴平行四边形ABCD是矩形.
A
B
C
D
例题讲解
例2 已知:如图,在矩形ABCD中,E,F,G,H 分别为OA,OB,OC,OD的中点. 求证:四边形EFGH是矩形.
B
C
D
E
F
G
H
O
A
证明:∵四边形ABCD是矩形,
∴AC=BD.且 OA=OC,OB=OD.
∴OA=OC=OB=OD.
又∵E,F,G,H 分别为OA,OB,OC,OD 的中点,
∴OE=OG=OF=OH.
∴四边形EFGH是平行四边形.
又∵EG=OE+OG=OF+OH= HF,
∴四边形EFGH是矩形.
随堂演练
1. 如图,要使 ABCD成为矩形,需添加的条件是( )
A.AB=BC
B.AO=BO
C.∠1=∠2
D.AC⊥BD
B
2.如图,在Rt△ABC中,∠BAC=90°,P为边BC上一点,PE⊥AB于E,PF⊥AC于F,AP=4,则EF的值为( )
A.3
B.4
C.2.4
D.2.5
B
3. 如图,木工师傅要做一个矩形木框,做好以后测量得长AB=CD=80 cm,宽AD=BC=60 cm,对角线AC的长为1 m,则这个木框 (填“合格”或“不合格”),判定的依据是 .
合格
有一个角是直角的平行四边形是矩形
4. 如图,在 ABCD中,延长AD到点E,使DE=AD,连接EB,EC,DB,请你添加一个条件______________________,使四边形DBCE是矩形.
EB=DC(答案不唯一)
5. 如图所示,四边形ABCD是平行四边形,点E在CB的延长线上,且BE=BC,DE=DC,连接AE.
求证:四边形AEBD是矩形.
证明: ∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,CD=AB.
∵BC=BE,∴AD=BE.
又AD//BE,∴四边形AEBD是平行四边形.
∵DE=DC,∴AB=DE,
∴平行四边形AEBD是矩形.
课堂小结
矩形的判定方法:
平行四边形
四边形
矩形
对角线
互相平分
有三个角是直角
有一个角是直角
对角线相等
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
