冀教版数学九年级下册同步课件:29.3 第2课时 切线的判定(共19张PPT)
文档属性
| 名称 | 冀教版数学九年级下册同步课件:29.3 第2课时 切线的判定(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 587.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 13:27:52 | ||
图片预览


文档简介
(共19张PPT)
第二十九章 直线与圆的位置关系
29.3 第2课时 切线的判定
知识回顾
1.直线和圆有哪些位置关系?
相交、相切、相离
2.切线的性质是什么?
性质:圆的切线垂直于过切点的半径.
几何语言:如图所示,
∵直线l切☉O于T,
∴OT⊥l.
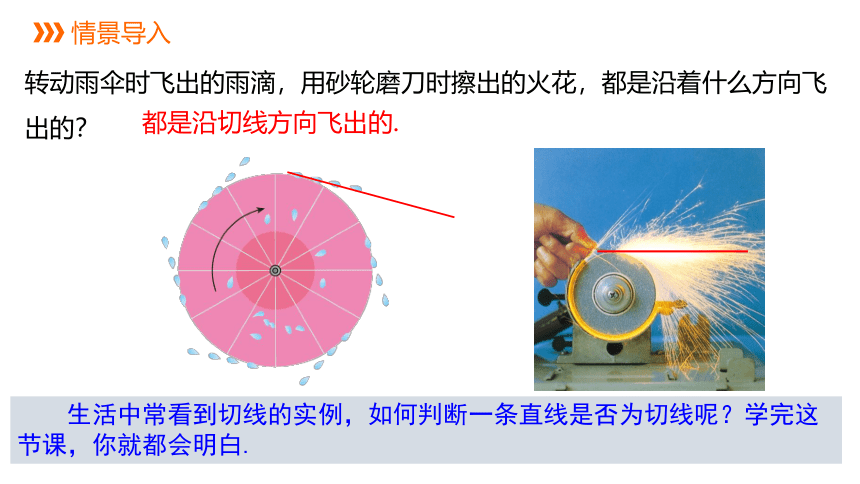
转动雨伞时飞出的雨滴,用砂轮磨刀时擦出的火花,都是沿着什么方向飞出的?
都是沿切线方向飞出的.
生活中常看到切线的实例,如何判断一条直线是否为切线呢?学完这节课,你就都会明白.
情景导入
直线与圆的三种位置关系中,图中直线l是⊙O的切线,
根据切线的定义可以判定一条直线是不是圆的切线,但有时使用定义判定很不方便.我们从另一个侧面去观察,那就是直线和圆的位置怎样时,直线也是圆的切线呢
怎样判定?
一起探究
获取新知
●O
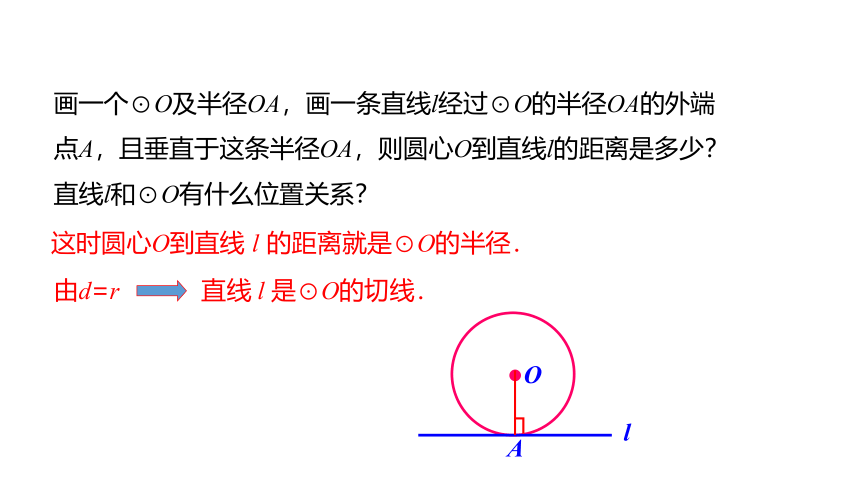
画一个⊙O及半径OA,画一条直线l经过⊙O的半径OA的外端点A,且垂直于这条半径OA,则圆心O到直线l的距离是多少?直线l和⊙O有什么位置关系?
┐
A
l
这时圆心O到直线 l 的距离就是⊙O的半径.
由d=r 直线 l 是⊙O的切线.
OA为⊙O的半径,
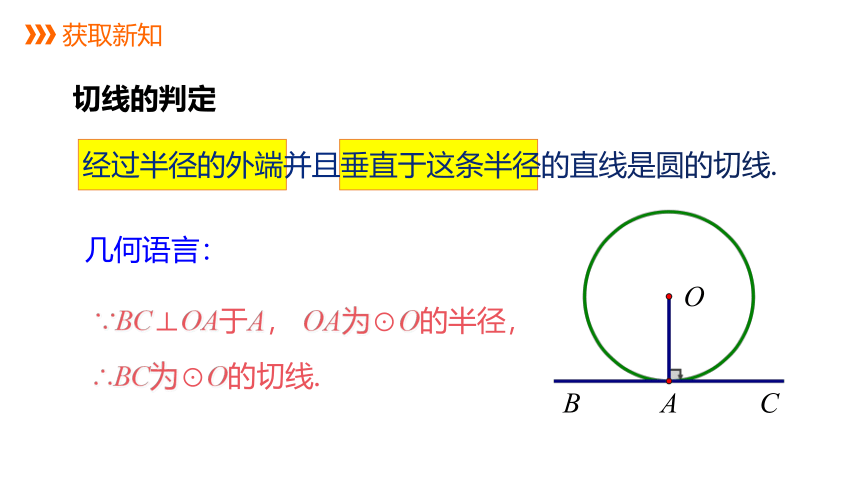
∵BC⊥OA于A,
∴BC为⊙O的切线.
几何语言:
切线的判定
O
A
C
B
经过半径的外端并且垂直于这条半径的直线是圆的切线.
获取新知
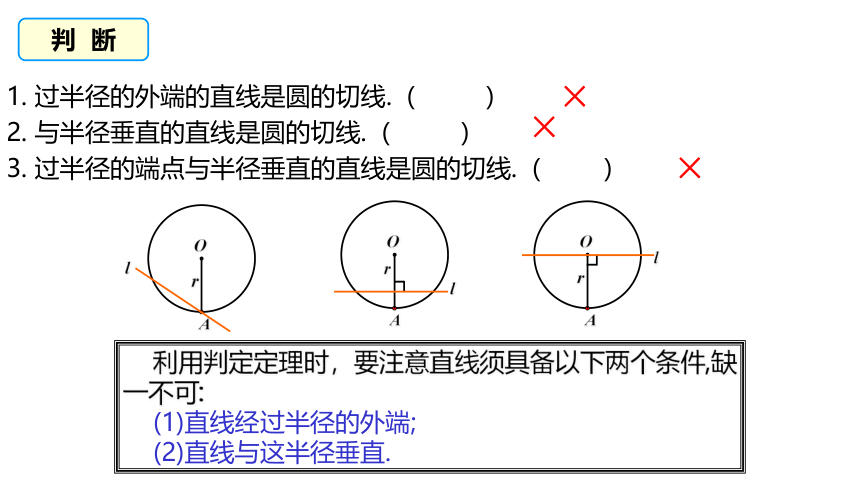
1. 过半径的外端的直线是圆的切线.( )
2. 与半径垂直的直线是圆的切线.( )
3. 过半径的端点与半径垂直的直线是圆的切线.( )
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这半径垂直.
判 断
判断一条直线是一个圆的切线有三个方法:
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线
l
A
l
O
l
r
d
归 纳
O
B
A
C
证明:连接OC(如图).
∵ OA=OB,CA=CB,
∴ OC是等腰三角形OAB底边AB上的中线.
∴ AB⊥OC.
∵ OC是⊙O的半径
∴ AB是⊙O的切线.
例题讲解
例1 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
连半径,证垂直
分析:由于AB过⊙O上的点C,所以连接OC,只要证明AB⊥OC即可.
O
A
B
C
D
证明:过点O作OE⊥AC于点E.
∵ AO平分∠BAC,OD⊥AB,
∴ OE=OD.
∵ OD是⊙O的半径,
∴ AC是⊙O的切线.
E
例2 已知:O为∠BAC平分线上一点,OD⊥AB于点D,以点O为
圆心,OD为半径作⊙O.
求证:⊙O与AC相切.
做垂直,证相等
分析:由点O向AC作垂线段OF,d=OF,r=OE,因此只需要证明OF=OE.
(1) 有交点,连半径,证垂直;
(2) 无交点,作垂直,证半径.
证切线时辅助线的添加方法
有切线时常用辅助线添加方法
见切点,连半径,得垂直.
切线的其他重要结论
(1)经过圆心且垂直于切线的直线必经过切点;
(2)经过切点且垂直于切线的直线必经过圆心.
总结提升
切线的画法
l
O
P
1.连接OP;
2.过点P画l⊥OP,直线l为所画.
获取新知
类型一 如图,P为⊙O上的一点,请你用三角尺画出这个圆过点P切线.
l’
O
类型二 如图,点A是⊙O外一点,过点A作⊙O的切线l
l
A
1、直角三角板的一直角边经过点O
2、平移三角板,使其另一直角边经过点A
3、画直线l
M
N
1.下列四个命题:
①与圆有公共点的直线是圆的切线;
②垂直于圆的半径的直线是圆的切线;
③到圆心的距离等于半径的直线是圆的切线;
④过直径端点,且垂直于此直径的直线是圆的切线.
其中是真命题的是( )
A.①② B.②③ C.③④ D.①④
C
随堂演练
2.如图所示,A是☉O上一点,且AO=5,PO=13,AP=12,则PA与☉O的位置关系是 .
A
P
O
相切
3. 如图,A,B是☉O上的两点,AC是过点A的一条直线.如果∠AOB=120°,那么当∠CAB的度数为 时,AC才能成为☉O的切线.
60°
3.如图,在⊙O中,AB=OA,P是半径OB延长线上一点,且PB=OB,PA与⊙O的位置关系是________.
相切
4.如图,AB是⊙O的直径,点C为⊙O上一点,过点B作BD⊥CD,垂足为点D,连接BC,BC平分∠ABD.
求证:CD为⊙O的切线.
∴CD为⊙O的切线.
证明: ∵BC平分∠ABD,
∴∠OBC=∠DBC.
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OCB=∠DBC,
∴OC∥BD.
∵BD⊥CD,
∴OC⊥CD,
5.如图,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E.
求证:CD与小圆相切.
证明:连结OE,过O作OF⊥CD,垂足为F.
∵AB与小圆O切于点E,∴OE⊥AB.
又∵AB=CD,
∴OF=OE,又OF⊥CD,
∴CD与小圆O相切.
F
课堂小结
第二十九章 直线与圆的位置关系
29.3 第2课时 切线的判定
知识回顾
1.直线和圆有哪些位置关系?
相交、相切、相离
2.切线的性质是什么?
性质:圆的切线垂直于过切点的半径.
几何语言:如图所示,
∵直线l切☉O于T,
∴OT⊥l.
转动雨伞时飞出的雨滴,用砂轮磨刀时擦出的火花,都是沿着什么方向飞出的?
都是沿切线方向飞出的.
生活中常看到切线的实例,如何判断一条直线是否为切线呢?学完这节课,你就都会明白.
情景导入
直线与圆的三种位置关系中,图中直线l是⊙O的切线,
根据切线的定义可以判定一条直线是不是圆的切线,但有时使用定义判定很不方便.我们从另一个侧面去观察,那就是直线和圆的位置怎样时,直线也是圆的切线呢
怎样判定?
一起探究
获取新知
●O
画一个⊙O及半径OA,画一条直线l经过⊙O的半径OA的外端点A,且垂直于这条半径OA,则圆心O到直线l的距离是多少?直线l和⊙O有什么位置关系?
┐
A
l
这时圆心O到直线 l 的距离就是⊙O的半径.
由d=r 直线 l 是⊙O的切线.
OA为⊙O的半径,
∵BC⊥OA于A,
∴BC为⊙O的切线.
几何语言:
切线的判定
O
A
C
B
经过半径的外端并且垂直于这条半径的直线是圆的切线.
获取新知
1. 过半径的外端的直线是圆的切线.( )
2. 与半径垂直的直线是圆的切线.( )
3. 过半径的端点与半径垂直的直线是圆的切线.( )
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这半径垂直.
判 断
判断一条直线是一个圆的切线有三个方法:
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线
l
A
l
O
l
r
d
归 纳
O
B
A
C
证明:连接OC(如图).
∵ OA=OB,CA=CB,
∴ OC是等腰三角形OAB底边AB上的中线.
∴ AB⊥OC.
∵ OC是⊙O的半径
∴ AB是⊙O的切线.
例题讲解
例1 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
连半径,证垂直
分析:由于AB过⊙O上的点C,所以连接OC,只要证明AB⊥OC即可.
O
A
B
C
D
证明:过点O作OE⊥AC于点E.
∵ AO平分∠BAC,OD⊥AB,
∴ OE=OD.
∵ OD是⊙O的半径,
∴ AC是⊙O的切线.
E
例2 已知:O为∠BAC平分线上一点,OD⊥AB于点D,以点O为
圆心,OD为半径作⊙O.
求证:⊙O与AC相切.
做垂直,证相等
分析:由点O向AC作垂线段OF,d=OF,r=OE,因此只需要证明OF=OE.
(1) 有交点,连半径,证垂直;
(2) 无交点,作垂直,证半径.
证切线时辅助线的添加方法
有切线时常用辅助线添加方法
见切点,连半径,得垂直.
切线的其他重要结论
(1)经过圆心且垂直于切线的直线必经过切点;
(2)经过切点且垂直于切线的直线必经过圆心.
总结提升
切线的画法
l
O
P
1.连接OP;
2.过点P画l⊥OP,直线l为所画.
获取新知
类型一 如图,P为⊙O上的一点,请你用三角尺画出这个圆过点P切线.
l’
O
类型二 如图,点A是⊙O外一点,过点A作⊙O的切线l
l
A
1、直角三角板的一直角边经过点O
2、平移三角板,使其另一直角边经过点A
3、画直线l
M
N
1.下列四个命题:
①与圆有公共点的直线是圆的切线;
②垂直于圆的半径的直线是圆的切线;
③到圆心的距离等于半径的直线是圆的切线;
④过直径端点,且垂直于此直径的直线是圆的切线.
其中是真命题的是( )
A.①② B.②③ C.③④ D.①④
C
随堂演练
2.如图所示,A是☉O上一点,且AO=5,PO=13,AP=12,则PA与☉O的位置关系是 .
A
P
O
相切
3. 如图,A,B是☉O上的两点,AC是过点A的一条直线.如果∠AOB=120°,那么当∠CAB的度数为 时,AC才能成为☉O的切线.
60°
3.如图,在⊙O中,AB=OA,P是半径OB延长线上一点,且PB=OB,PA与⊙O的位置关系是________.
相切
4.如图,AB是⊙O的直径,点C为⊙O上一点,过点B作BD⊥CD,垂足为点D,连接BC,BC平分∠ABD.
求证:CD为⊙O的切线.
∴CD为⊙O的切线.
证明: ∵BC平分∠ABD,
∴∠OBC=∠DBC.
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OCB=∠DBC,
∴OC∥BD.
∵BD⊥CD,
∴OC⊥CD,
5.如图,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E.
求证:CD与小圆相切.
证明:连结OE,过O作OF⊥CD,垂足为F.
∵AB与小圆O切于点E,∴OE⊥AB.
又∵AB=CD,
∴OF=OE,又OF⊥CD,
∴CD与小圆O相切.
F
课堂小结
