冀教版数学九年级下册同步课件:30.2 第1课时 二次函数y=ax2的图像和性质(共22张PPT)
文档属性
| 名称 | 冀教版数学九年级下册同步课件:30.2 第1课时 二次函数y=ax2的图像和性质(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 331.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
第三十章 二次函数
30.2 第1课时 二次函数y=ax 的图像和性质
一条直线
②影响直线的有哪些因素?
k影响直线的上升、下降趋势.
当k>0时,直线自左向右呈上升趋势.
当k<0时,直线自左向右呈下降趋势.
b影响直线与y轴的交点.
当b>0,b=0,b<0时,直线与y轴的交点分别在y轴的正半轴,过原点,y轴的负半轴.
k和b
问题1: 一次函数 的图像是什么?
①
复习导入
双曲线
②影响双曲线的因素是什么?
当k>0时,双曲线位于第一、三象限,在每一象限内,y随x的增大而减小.
当k<0时,双曲线位于第二、四象限,在每一象限内,y随x的增大而增大.
常数k
问题2: 反函数 的图像是什么?
①
思考:
由前面的结论可知,常数a、b、c对于二次函数的图像都会产生影响.
常数a、b、c
对于二次函数 来说,影响其
图像的因素是哪些?
获取新知
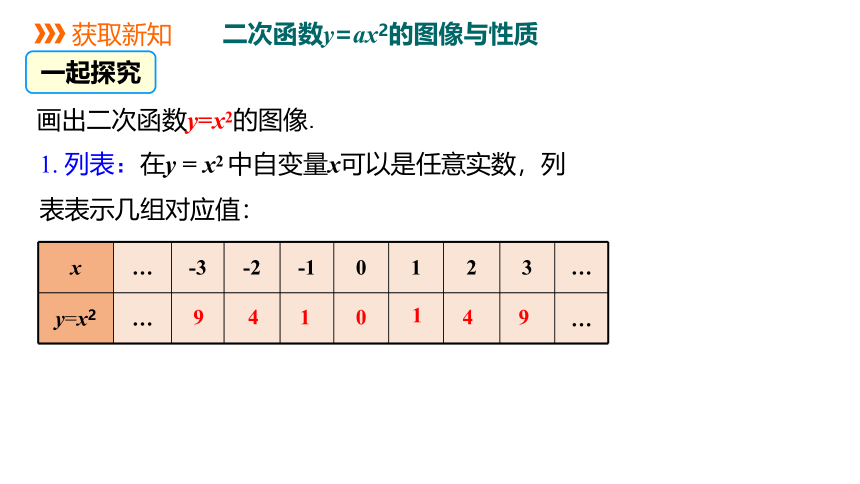
画出二次函数y=x2的图像.
1. 列表:在y = x2 中自变量x可以是任意实数,列表表示几组对应值:
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
9
4
1
0
1
9
4
二次函数y=ax2的图像与性质
一起探究
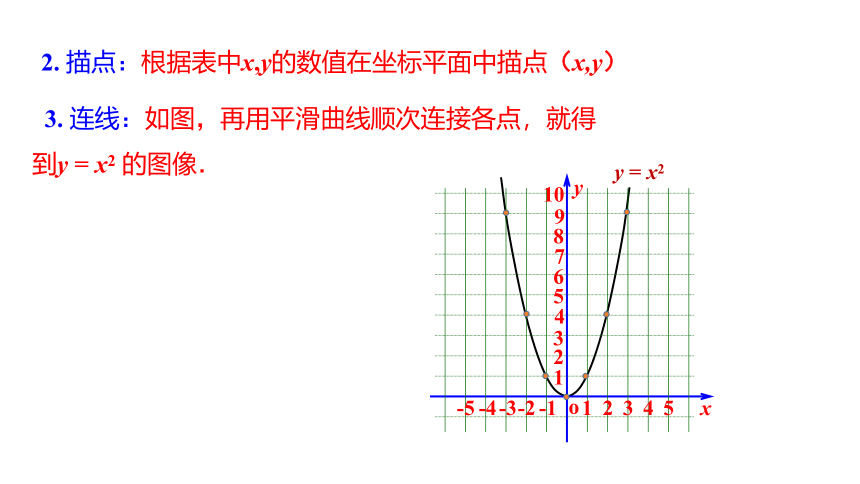
2. 描点:根据表中x,y的数值在坐标平面中描点(x,y)
3. 连线:如图,再用平滑曲线顺次连接各点,就得到y = x2 的图像.
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
y = x2
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
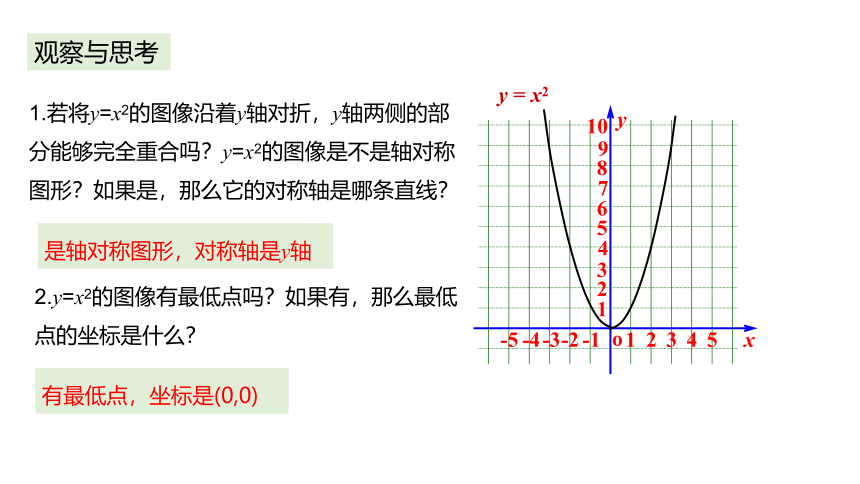
观察与思考
1.若将y=x2的图像沿着y轴对折,y轴两侧的部分能够完全重合吗?y=x2的图像是不是轴对称图形?如果是,那么它的对称轴是哪条直线?
2.y=x2的图像有最低点吗?如果有,那么最低点的坐标是什么?
是轴对称图形,对称轴是y轴
有最低点,坐标是(0,0)
y = x2
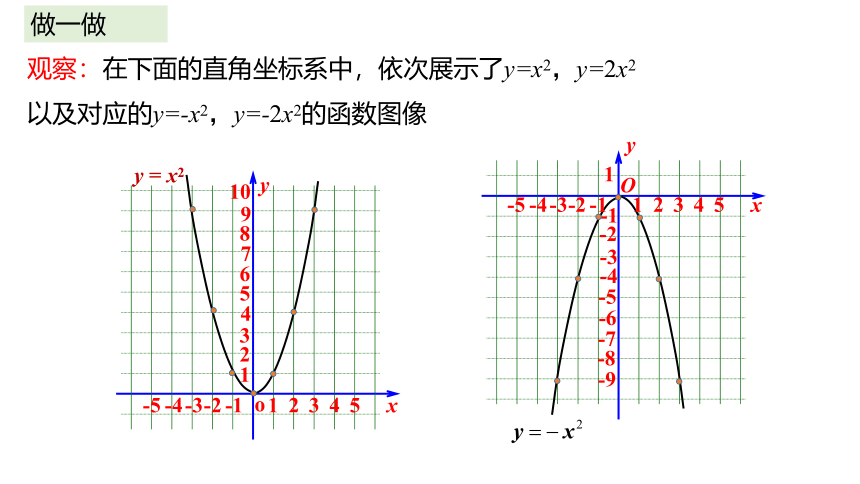
观察:在下面的直角坐标系中,依次展示了y=x2,y=2x2以及对应的y=-x2,y=-2x2的函数图像
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
y = x2
1
2
3
4
5
x
1
O
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
-6
-7
-8
-9
y
做一做
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
0
-1
-2
-3
-4
-5
y = 2x2
x
1
y
-2
-4
-6
0
2
4
6
-2
-4
-6
-8
-10
思考:对比函数y=x2与y=-x2,以及y=2x2与y=-2x2的图像
(1)图像的开口方向和它的最高(或最低)点与a的符号具有怎样的关系呢?
(2)图像是不是轴对称图形呢?如果是,那么它的对称轴是那条直线呢?
a>0,开口向上,有最高点;
a<0,开口向下,有最低点
图像是轴对称图形,对称轴是y轴
(3)根据图像,说明y的值随x的值的增大而变化的情况.
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
y = x2
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
0
-1
-2
-3
-4
-5
y = 2x2
(a>0) 当x>0时,y随x取值的增大而增大;
当x<0时,y随x取值的增大而减小.
y
1
2
3
4
5
x
1
O
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
-6
-7
-8
-9
x
1
y
-2
-4
-6
0
2
4
6
-2
-4
-6
-8
-10
(a<0)当x>0时,y随x取值的增大而减小;
当x<0时,y随x取值的增大而增大.
二次函数y=ax2 的图像是一条关于y轴对称的曲线,
这样的曲线叫做抛物线,曲线的对称轴叫做抛物线
的对称轴,抛物线与它的对称轴的交点叫做抛物线
的顶点.
知识要点
y=ax2 a>0 a<0
图象
位置开
口方向
对称性
顶点最值
增减性
开口向上,在x轴上方
开口向下,在x轴下方
关于y轴对称,对称轴是直线x=0
顶点坐标是原点(0,0)
当x=0时,y最小值=0
当x=0时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
y
O
x
y
O
x
归 纳
二次函数y=ax2的图像与性质
为了方便起见,我们把y轴记为直线x=0,把过点(a,0)且垂直于x轴的直线记为直线x=a;
把x轴记为直线y=0,把过点(0,b)且垂直于y轴的直线记为直线y=b
例1.一个二次函数,它的图像的顶点是原点,对称轴是y轴,且经过点(1, )
(1)求这个二次函数的解析式;
(2)画出这个二次函数的图像;
(3)根据图像指出,当x>0时,若x增大,y怎样变化?当x<0时,若x增大,y怎样变化?
(4)当x取何值时,y有最大(或最小)值,其值为多少?
例题讲解
(1)求这个二次函数的解析式;
分析:
由已知中二次函数图像顶点为原点,对称轴为y轴,可推断此函数符合
解:设这个二次函数解析式为
(2)画出这个二次函数的图像;
(3)根据图像指出,当x>0时,若x增大,y怎样变化?当x<0时,若x增大,y怎样变化?
当x>0时,y随x增大而增大;当x<0时, y随x增大而减小;
(4)当x取何值时,y有最大(或最小)值,其值为多少?
当x=0时,y有最小值为0.
随堂演练
1. 下列关于函数y=36x2的叙述中,错误的是( )
A.图像的对称轴是y轴
B.图像的顶点是原点
C.当x>0时,y随x的增大而增大
D.y有最大值
D
2.函数y=-3x2的图像的开口 , 对称轴 ,顶点是 ;在对称轴的左侧, y随x的增大而 ,在对称轴的右侧, y随x的增大而 .
向下
y轴
(0,0)
减小
增大
3. 如右图,观察函数y=( k-1)x2的图像,则k的取值范围是 .
x
y
k>1
4.说出下列抛物线的开口方向、对称轴和顶点:
开口方向
对称轴
顶点
向上
向下
向下
向上
y轴
y轴
y轴
y轴
(0,0)
(0,0)
(0,0)
(0,0)
课堂小结
二次函数y=ax2的图像及性质
画法
描点法
以对称轴为中心对称取点
图像
抛物线
轴对称图形
性质
重点关注4个方面
开口方向及大小
对称轴
顶点坐标
增减性
第三十章 二次函数
30.2 第1课时 二次函数y=ax 的图像和性质
一条直线
②影响直线的有哪些因素?
k影响直线的上升、下降趋势.
当k>0时,直线自左向右呈上升趋势.
当k<0时,直线自左向右呈下降趋势.
b影响直线与y轴的交点.
当b>0,b=0,b<0时,直线与y轴的交点分别在y轴的正半轴,过原点,y轴的负半轴.
k和b
问题1: 一次函数 的图像是什么?
①
复习导入
双曲线
②影响双曲线的因素是什么?
当k>0时,双曲线位于第一、三象限,在每一象限内,y随x的增大而减小.
当k<0时,双曲线位于第二、四象限,在每一象限内,y随x的增大而增大.
常数k
问题2: 反函数 的图像是什么?
①
思考:
由前面的结论可知,常数a、b、c对于二次函数的图像都会产生影响.
常数a、b、c
对于二次函数 来说,影响其
图像的因素是哪些?
获取新知
画出二次函数y=x2的图像.
1. 列表:在y = x2 中自变量x可以是任意实数,列表表示几组对应值:
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
9
4
1
0
1
9
4
二次函数y=ax2的图像与性质
一起探究
2. 描点:根据表中x,y的数值在坐标平面中描点(x,y)
3. 连线:如图,再用平滑曲线顺次连接各点,就得到y = x2 的图像.
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
y = x2
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
观察与思考
1.若将y=x2的图像沿着y轴对折,y轴两侧的部分能够完全重合吗?y=x2的图像是不是轴对称图形?如果是,那么它的对称轴是哪条直线?
2.y=x2的图像有最低点吗?如果有,那么最低点的坐标是什么?
是轴对称图形,对称轴是y轴
有最低点,坐标是(0,0)
y = x2
观察:在下面的直角坐标系中,依次展示了y=x2,y=2x2以及对应的y=-x2,y=-2x2的函数图像
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
y = x2
1
2
3
4
5
x
1
O
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
-6
-7
-8
-9
y
做一做
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
0
-1
-2
-3
-4
-5
y = 2x2
x
1
y
-2
-4
-6
0
2
4
6
-2
-4
-6
-8
-10
思考:对比函数y=x2与y=-x2,以及y=2x2与y=-2x2的图像
(1)图像的开口方向和它的最高(或最低)点与a的符号具有怎样的关系呢?
(2)图像是不是轴对称图形呢?如果是,那么它的对称轴是那条直线呢?
a>0,开口向上,有最高点;
a<0,开口向下,有最低点
图像是轴对称图形,对称轴是y轴
(3)根据图像,说明y的值随x的值的增大而变化的情况.
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
y = x2
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
0
-1
-2
-3
-4
-5
y = 2x2
(a>0) 当x>0时,y随x取值的增大而增大;
当x<0时,y随x取值的增大而减小.
y
1
2
3
4
5
x
1
O
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
-6
-7
-8
-9
x
1
y
-2
-4
-6
0
2
4
6
-2
-4
-6
-8
-10
(a<0)当x>0时,y随x取值的增大而减小;
当x<0时,y随x取值的增大而增大.
二次函数y=ax2 的图像是一条关于y轴对称的曲线,
这样的曲线叫做抛物线,曲线的对称轴叫做抛物线
的对称轴,抛物线与它的对称轴的交点叫做抛物线
的顶点.
知识要点
y=ax2 a>0 a<0
图象
位置开
口方向
对称性
顶点最值
增减性
开口向上,在x轴上方
开口向下,在x轴下方
关于y轴对称,对称轴是直线x=0
顶点坐标是原点(0,0)
当x=0时,y最小值=0
当x=0时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
y
O
x
y
O
x
归 纳
二次函数y=ax2的图像与性质
为了方便起见,我们把y轴记为直线x=0,把过点(a,0)且垂直于x轴的直线记为直线x=a;
把x轴记为直线y=0,把过点(0,b)且垂直于y轴的直线记为直线y=b
例1.一个二次函数,它的图像的顶点是原点,对称轴是y轴,且经过点(1, )
(1)求这个二次函数的解析式;
(2)画出这个二次函数的图像;
(3)根据图像指出,当x>0时,若x增大,y怎样变化?当x<0时,若x增大,y怎样变化?
(4)当x取何值时,y有最大(或最小)值,其值为多少?
例题讲解
(1)求这个二次函数的解析式;
分析:
由已知中二次函数图像顶点为原点,对称轴为y轴,可推断此函数符合
解:设这个二次函数解析式为
(2)画出这个二次函数的图像;
(3)根据图像指出,当x>0时,若x增大,y怎样变化?当x<0时,若x增大,y怎样变化?
当x>0时,y随x增大而增大;当x<0时, y随x增大而减小;
(4)当x取何值时,y有最大(或最小)值,其值为多少?
当x=0时,y有最小值为0.
随堂演练
1. 下列关于函数y=36x2的叙述中,错误的是( )
A.图像的对称轴是y轴
B.图像的顶点是原点
C.当x>0时,y随x的增大而增大
D.y有最大值
D
2.函数y=-3x2的图像的开口 , 对称轴 ,顶点是 ;在对称轴的左侧, y随x的增大而 ,在对称轴的右侧, y随x的增大而 .
向下
y轴
(0,0)
减小
增大
3. 如右图,观察函数y=( k-1)x2的图像,则k的取值范围是 .
x
y
k>1
4.说出下列抛物线的开口方向、对称轴和顶点:
开口方向
对称轴
顶点
向上
向下
向下
向上
y轴
y轴
y轴
y轴
(0,0)
(0,0)
(0,0)
(0,0)
课堂小结
二次函数y=ax2的图像及性质
画法
描点法
以对称轴为中心对称取点
图像
抛物线
轴对称图形
性质
重点关注4个方面
开口方向及大小
对称轴
顶点坐标
增减性
