冀教版数学九年级下册同步课件:30.1 二次函数(共21张PPT)
文档属性
| 名称 | 冀教版数学九年级下册同步课件:30.1 二次函数(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 833.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
第三十章 二次函数
30.1 二次函数
问题1 什么叫函数
一般地,在一个变化的过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
一般地,形如y=kx+b(k,b是常数,k≠0)的函数叫做一次函数.
当b=0 时,一次函数y=kx就叫做正比例函数.
问题2 什么是一次函数?正比例函数?
知识回顾
问题3 我们探究一次函数、反比例函数时的思路是什么
定义→图象和性质→应用
情景导入
雨后天空的彩虹,公园里的喷泉,跳绳等都会形成一条曲线.这些曲线能否用函数关系式表示?
图片欣赏
问题1 如图所示,用规格相同的正方形瓷砖铺成矩形地面,其中,横向瓷砖比纵向瓷砖每排多5块,矩形地面最外面一圈为红色瓷砖,其余部分全为白色瓷砖.设纵向每排有n块瓷砖.
(1)设红色瓷砖的总数为y块.
①用含n的代数式表示y,
则y= .
②y与n具有怎样的函数关系
4n+6
一次函数
获取新知
一起探究
二次函数的概念
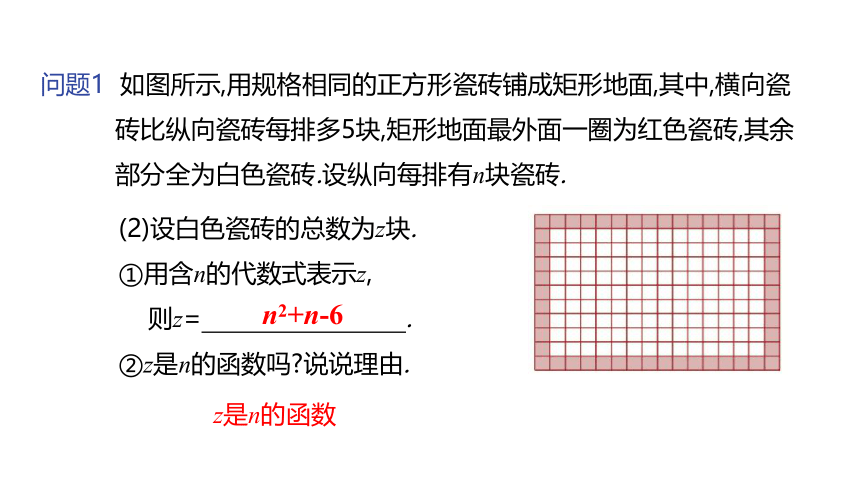
(2)设白色瓷砖的总数为z块.
①用含n的代数式表示z,
则z= .
②z是n的函数吗 说说理由.
z是n的函数
问题1 如图所示,用规格相同的正方形瓷砖铺成矩形地面,其中,横向瓷砖比纵向瓷砖每排多5块,矩形地面最外面一圈为红色瓷砖,其余部分全为白色瓷砖.设纵向每排有n块瓷砖.
n2+n-6
问题2 某企业今年第一季度的产值为80万元,预计产值的季平均增长率为x.
分析:
(1)设第二季度的产值为y万元,则y= .
设第三季度的产值为z万元,则z= .
(2)y,z都是x的函数吗 它们的表达式有什么不同
80x+80
80x2+160x+80
y=80x+80,一次函数.
z=80x2+160x+80,自变量x的最高次数是二次的.
问题3 观察下面两个函数:z=n2+n-6,z=80x2+160x+80,
(1)这两个函数与我们学过的函数有什么不同
函数式右边关于自变量的二次式,由二次项,一次项,常数项之和构成
(2)这两个函数的自变量x的最高指数分别是多少
二次
(3)你能说出函数表达式右边的二次项,一次项,常数项及二次项系数,一次项系数吗
函数:z=n2+n-6中二次项,一次项,常数项分别为n2,n,-6
二次项系数,一次项系数分别为1,1
函数:z=80x2+160x+80中二次项,一次项,常数项分别为80x2,160x,80
二次项系数,一次项系数分别为80,160
形成概念
归纳出这种函数的一般形式
为:y=ax2+bx+c
概念学习
定义:一般地,如果两个变量x和y之间的函数关系可以表示成y=ax2+bx+c(a,b,c是常数,且a≠0),那么称y为x的二次函数.其中,a叫做二次项系数,b叫做一次项系数,c叫做常数项.
二次函数的定义:
温馨提示:
(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠ 0;
(3)等式的右边最高次数为 2,可以没有一次项和常数项,但不能没有二次项.
例题讲解
例1 下列函数中,哪些是二次函数?并指出二次函
数的二次项系数、一次项系数和常数项.
(1)y=7x-1; (2)y=-5x2;
(3)y=3a3+2a2; (4)y=x-2+x;
(5)y=3(x-2)(x-5); (6)y=x2+ .
(1)y=7x-1;
×
(2)y=-5x2;
√
(3)y=3a3+2a2;
×
自变量的最高次数是1
自变量的最高次数是2
自变量的最高次数是3
(4)y=x-2+x;
x-2不是整式
×
(5)y=3(x-2)(x-5);
整理得到y=3x2-21x+30,是二次函数
√
×
(6)y=x2+
不是整式
二次项系数
解:(2) y=-5x2
所以y=-5x2的二次项系数为-5,一次项系
数为0,常数项为0.
(5)化为一般式,得到y=3x2-21x+30,
所以y=3(x-2)(x-5)的二次项系数为3,
一次项系数为-21,常数项为30.
二次项系数
一次项系数
常数项
判断一个函数是不是二次函数,先看原函数和整理化简后的形式再作判断.除此之外,二次函数除有一般形式y=ax2+bx+c(a≠0)外,还有其特殊形式如y=ax2,y=ax2+bx, y=ax2+c等.
方法归纳
获取新知
列二次函数表达式
做一做 新学期开学,全班同学见面时相互亲切握手问候.设全班有m名 同学,每两人之间都握手一次,用y表示全班同学握手的总次数.
(1)请用含m的代数式表示y,说明y是m的二次函数,指出该函数中对应的a,b,c的值.
(2)若全班有45名同学,则这样握手的总次数是多少
解:(1) .因为m的最高次数是2,
所以y是m的二次函数,对应的a,b,c的值依次为
(2)当m=45时, .
例2 填空:
(1)已知圆柱的高为14 cm,则圆柱的体积V(cm3)与底面半径r(cm)之间的函数关系式是_______________;
(2)已知正方形的边长为10,若边长减少x,则面积减少y,
y与x之间的函数关系式是_____________________.
V=14πr2(r>0)
y=-x2+20x(0≤x≤10)
例题讲解
根据实际问题列二次函数的表达式应注意:
(1)正确辨别自变量与因变量;
(2)确保找到正确的等量关系;
(3)将列出的关系式整理成y=ax2+bx+c(a≠0)的形式;
(4)确保自变量有意义.
方法归纳
B
1.下列函数:
①y=2(x-1)(x+4);
②y=3(x-1)2+2;
③y=x2+ +1;
④y=(x-3)2-x2.
其中不是二次函数的是( )
A.①② B.③④ C.①③ D.②④
随堂演练
2.若函数y=(m-2)x2+4x-5(m是常数)是二次函数,则( )
A.m≠-2 B.m≠2 C.m≠3 D.m≠-3
B
3. 已知二次函数y=1-3x+5x2,则它的二次项系数a,
一次项系数b,常数项c分别是( )
A.a=1,b=-3,c=5
B.a=1,b=3,c=5
C.a=5,b=3,c=1
D.a=5,b=-3,c=1
D
4.已知二次函数y=1-2x-x2,其中二次项系数a=_____,一次项系数b=_____,常数项c=_____.
5.对于二次函数y=x2+3x-2,当x=-1时,y的值为_____,
当y=8时,x的值为 .
1
-1
-2
2或-5
-4
6.矩形的周长为16cm,它的一边长为x cm,面积为y cm2.求(1)y与x之间的函数解析式及自变量x的取值范围;
(2)当x=3时矩形的面积.
解:(1)y=(8-x)x=-x2+8x (0<x<8);
(2)当x=3时,y=-32+8×3=15 (cm2 ).
课堂小结
二次函数
定 义
y=ax2+bx+c(a ≠0,
a,b,c是常数)
一般形式
右边是整式;
自变量的最高次数是2;
二次项系数a ≠0.
确定二次项系数,
一次项系数,
常数项
列二次函数的表达式
注意:自变量的取值范围
第三十章 二次函数
30.1 二次函数
问题1 什么叫函数
一般地,在一个变化的过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
一般地,形如y=kx+b(k,b是常数,k≠0)的函数叫做一次函数.
当b=0 时,一次函数y=kx就叫做正比例函数.
问题2 什么是一次函数?正比例函数?
知识回顾
问题3 我们探究一次函数、反比例函数时的思路是什么
定义→图象和性质→应用
情景导入
雨后天空的彩虹,公园里的喷泉,跳绳等都会形成一条曲线.这些曲线能否用函数关系式表示?
图片欣赏
问题1 如图所示,用规格相同的正方形瓷砖铺成矩形地面,其中,横向瓷砖比纵向瓷砖每排多5块,矩形地面最外面一圈为红色瓷砖,其余部分全为白色瓷砖.设纵向每排有n块瓷砖.
(1)设红色瓷砖的总数为y块.
①用含n的代数式表示y,
则y= .
②y与n具有怎样的函数关系
4n+6
一次函数
获取新知
一起探究
二次函数的概念
(2)设白色瓷砖的总数为z块.
①用含n的代数式表示z,
则z= .
②z是n的函数吗 说说理由.
z是n的函数
问题1 如图所示,用规格相同的正方形瓷砖铺成矩形地面,其中,横向瓷砖比纵向瓷砖每排多5块,矩形地面最外面一圈为红色瓷砖,其余部分全为白色瓷砖.设纵向每排有n块瓷砖.
n2+n-6
问题2 某企业今年第一季度的产值为80万元,预计产值的季平均增长率为x.
分析:
(1)设第二季度的产值为y万元,则y= .
设第三季度的产值为z万元,则z= .
(2)y,z都是x的函数吗 它们的表达式有什么不同
80x+80
80x2+160x+80
y=80x+80,一次函数.
z=80x2+160x+80,自变量x的最高次数是二次的.
问题3 观察下面两个函数:z=n2+n-6,z=80x2+160x+80,
(1)这两个函数与我们学过的函数有什么不同
函数式右边关于自变量的二次式,由二次项,一次项,常数项之和构成
(2)这两个函数的自变量x的最高指数分别是多少
二次
(3)你能说出函数表达式右边的二次项,一次项,常数项及二次项系数,一次项系数吗
函数:z=n2+n-6中二次项,一次项,常数项分别为n2,n,-6
二次项系数,一次项系数分别为1,1
函数:z=80x2+160x+80中二次项,一次项,常数项分别为80x2,160x,80
二次项系数,一次项系数分别为80,160
形成概念
归纳出这种函数的一般形式
为:y=ax2+bx+c
概念学习
定义:一般地,如果两个变量x和y之间的函数关系可以表示成y=ax2+bx+c(a,b,c是常数,且a≠0),那么称y为x的二次函数.其中,a叫做二次项系数,b叫做一次项系数,c叫做常数项.
二次函数的定义:
温馨提示:
(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠ 0;
(3)等式的右边最高次数为 2,可以没有一次项和常数项,但不能没有二次项.
例题讲解
例1 下列函数中,哪些是二次函数?并指出二次函
数的二次项系数、一次项系数和常数项.
(1)y=7x-1; (2)y=-5x2;
(3)y=3a3+2a2; (4)y=x-2+x;
(5)y=3(x-2)(x-5); (6)y=x2+ .
(1)y=7x-1;
×
(2)y=-5x2;
√
(3)y=3a3+2a2;
×
自变量的最高次数是1
自变量的最高次数是2
自变量的最高次数是3
(4)y=x-2+x;
x-2不是整式
×
(5)y=3(x-2)(x-5);
整理得到y=3x2-21x+30,是二次函数
√
×
(6)y=x2+
不是整式
二次项系数
解:(2) y=-5x2
所以y=-5x2的二次项系数为-5,一次项系
数为0,常数项为0.
(5)化为一般式,得到y=3x2-21x+30,
所以y=3(x-2)(x-5)的二次项系数为3,
一次项系数为-21,常数项为30.
二次项系数
一次项系数
常数项
判断一个函数是不是二次函数,先看原函数和整理化简后的形式再作判断.除此之外,二次函数除有一般形式y=ax2+bx+c(a≠0)外,还有其特殊形式如y=ax2,y=ax2+bx, y=ax2+c等.
方法归纳
获取新知
列二次函数表达式
做一做 新学期开学,全班同学见面时相互亲切握手问候.设全班有m名 同学,每两人之间都握手一次,用y表示全班同学握手的总次数.
(1)请用含m的代数式表示y,说明y是m的二次函数,指出该函数中对应的a,b,c的值.
(2)若全班有45名同学,则这样握手的总次数是多少
解:(1) .因为m的最高次数是2,
所以y是m的二次函数,对应的a,b,c的值依次为
(2)当m=45时, .
例2 填空:
(1)已知圆柱的高为14 cm,则圆柱的体积V(cm3)与底面半径r(cm)之间的函数关系式是_______________;
(2)已知正方形的边长为10,若边长减少x,则面积减少y,
y与x之间的函数关系式是_____________________.
V=14πr2(r>0)
y=-x2+20x(0≤x≤10)
例题讲解
根据实际问题列二次函数的表达式应注意:
(1)正确辨别自变量与因变量;
(2)确保找到正确的等量关系;
(3)将列出的关系式整理成y=ax2+bx+c(a≠0)的形式;
(4)确保自变量有意义.
方法归纳
B
1.下列函数:
①y=2(x-1)(x+4);
②y=3(x-1)2+2;
③y=x2+ +1;
④y=(x-3)2-x2.
其中不是二次函数的是( )
A.①② B.③④ C.①③ D.②④
随堂演练
2.若函数y=(m-2)x2+4x-5(m是常数)是二次函数,则( )
A.m≠-2 B.m≠2 C.m≠3 D.m≠-3
B
3. 已知二次函数y=1-3x+5x2,则它的二次项系数a,
一次项系数b,常数项c分别是( )
A.a=1,b=-3,c=5
B.a=1,b=3,c=5
C.a=5,b=3,c=1
D.a=5,b=-3,c=1
D
4.已知二次函数y=1-2x-x2,其中二次项系数a=_____,一次项系数b=_____,常数项c=_____.
5.对于二次函数y=x2+3x-2,当x=-1时,y的值为_____,
当y=8时,x的值为 .
1
-1
-2
2或-5
-4
6.矩形的周长为16cm,它的一边长为x cm,面积为y cm2.求(1)y与x之间的函数解析式及自变量x的取值范围;
(2)当x=3时矩形的面积.
解:(1)y=(8-x)x=-x2+8x (0<x<8);
(2)当x=3时,y=-32+8×3=15 (cm2 ).
课堂小结
二次函数
定 义
y=ax2+bx+c(a ≠0,
a,b,c是常数)
一般形式
右边是整式;
自变量的最高次数是2;
二次项系数a ≠0.
确定二次项系数,
一次项系数,
常数项
列二次函数的表达式
注意:自变量的取值范围
