冀教版数学九年级下册同步课件:31.3 第2课时 用频率估计概率(共25张PPT)
文档属性
| 名称 | 冀教版数学九年级下册同步课件:31.3 第2课时 用频率估计概率(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 318.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 13:44:12 | ||
图片预览






文档简介
(共25张PPT)
第三十一章 随机事件的概率
31.3 第2课时 用频率估计概率
概率:一个数P(A)表示随机事件A发生的可能性大小, 称P(A)为事件A的概率.
P(A)=
频率:每个考察对象出现的次数与总次数的比值称为频率.
知识回顾
欣赏著名球星詹姆斯图片,你知道詹姆斯罚球命中率是多少吗
当试验的所有结果不是有限个,或各种可能结果发生的可能性不相等时,又该如何求事件发生的概率呢
情景导入
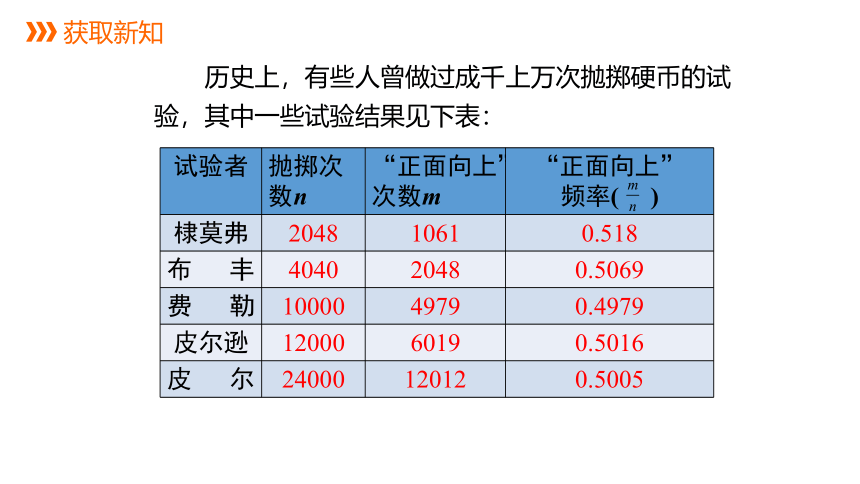
试验者 抛掷次数n “正面向上”次数m “正面向上”
频率( )
棣莫弗 2048 1061 0.518
布 丰 4040 2048 0.5069
费 勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮 尔 24000 12012 0.5005
历史上,有些人曾做过成千上万次抛掷硬币的试
验,其中一些试验结果见下表:
获取新知
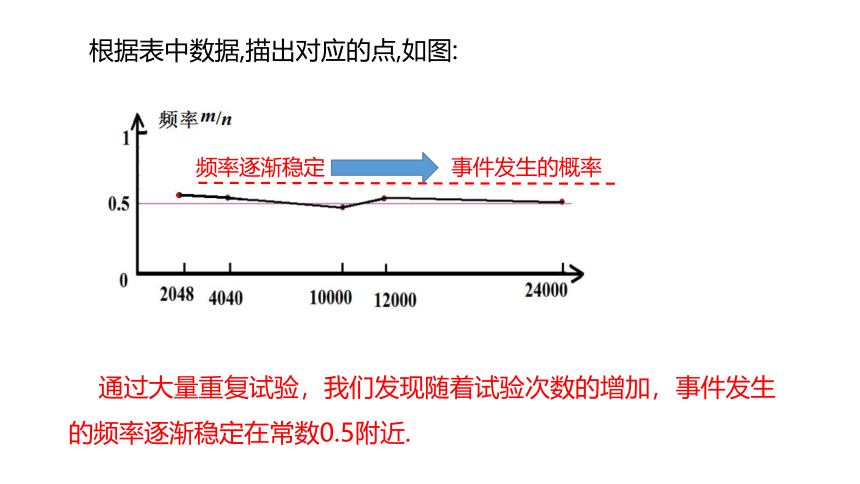
通过大量重复试验,我们发现随着试验次数的增加,事件发生的频率逐渐稳定在常数0.5附近.
根据表中数据,描出对应的点,如图:
频率逐渐稳定
事件发生的概率
数学史实
人们在长期的实践中发现,在随机试验中,由于众多微小的偶然因素的影响,每次测得的结果虽不尽相同,但大量重复试验所得结果却能反应客观规律.这称为大数法则,亦称大数定律.
频率稳定性定理
思考 抛掷硬币试验的特点:
1.可能出现的结果数__________;
2.每种可能结果的可能性__________.
相等
有限
问题 如果某一随机事件,可能出现的结果是无限个,或
每种可能结果发生的可能性不一致,那么我们无法用列
举法求其概率,这时我们能够用频率来估计概率吗?
一起探究
从一定高度落下的图钉,着地时会有哪些可能的结果?
其中顶帽着地的可能性大吗?
做做试验来解决这个问题.
图钉落地的试验
试验探究
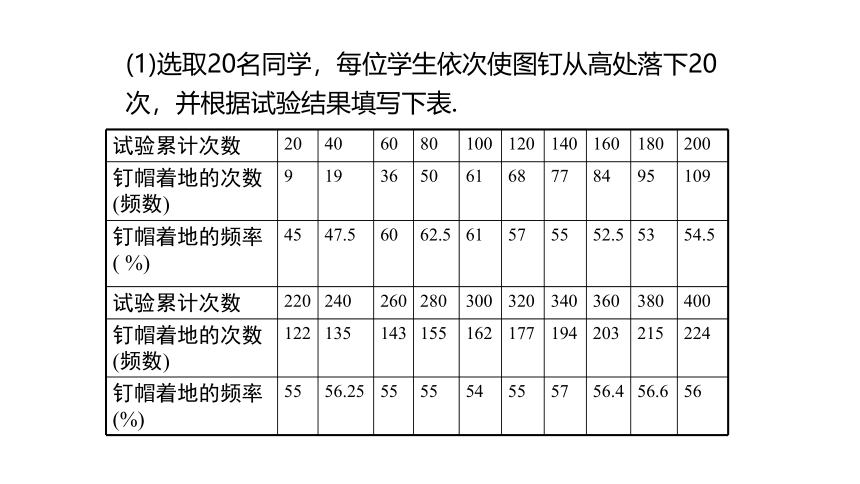
试验累计次数 20 40 60 80 100 120 140 160 180 200
钉帽着地的次数(频数) 9 19 36 50 61 68 77 84 95 109
钉帽着地的频率( %) 45 47.5 60 62.5 61 57 55 52.5 53 54.5
试验累计次数 220 240 260 280 300 320 340 360 380 400
钉帽着地的次数(频数) 122 135 143 155 162 177 194 203 215 224
钉帽着地的频率(%) 55 56.25 55 55 54 55 57 56.4 56.6 56
(1)选取20名同学,每位学生依次使图钉从高处落下20次,并根据试验结果填写下表.
56%
(%)
(2)根据上表画出统计图表示“顶帽着地”的频率.
(3)这个试验说明了什么问题.
在图钉落地试验中,“顶帽着地”的频率随着试验次数的增加,稳定在常数56%附近.
一般地,在大量重复试验中,随机事件A发生的频率 (这里n是实验总次数,它必须相当大,m是在n次试验中随机事件A发生的次数)会稳定到某个常数P.于是,我们用P这个常数表示事件A发生的概率,即P(A)=P.
归纳总结
则这个厂生产的瓷砖是合格品的概率估计值是______.(精确到0.01)
0.95
提示:运用频率和概率之间的关系,根据频率的波动情况估算概率.
例1 某瓷砖厂在相同条件下抽取部分瓷砖做耐磨试验,结果如下表所示:
例题讲解
例2 十一期间,某商场举行促销活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物20元以上就能获一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据:
转动转盘的次数 100 150 200 500 800 1 000
落在“圆珠笔”区域的次数 68 111 136 345 564 701
落在“圆珠笔”区域的频率
(1)计算并完成表格;
(2)请估计,当转动转盘的次数很大时,频率将会接近多少?
(3)假如你去转动该转盘一次,你获得圆珠笔的概率约是多少?
用落在“圆珠笔”区域的次数除以转动转盘的次数即是落在“圆珠笔”区域的频率,然后观察这组数趋向于哪个数,根据频率与概率的关系得出所求概率的值.
分析:
(1)
解:
转动转盘的次数 100 150 200 500 800 1 000
落在“圆珠笔”区域的次数 68 111 136 345 564 701
落在“圆珠笔”区域的频率 0.68 0.74 0.68 0.69 0.705 0.701
(2)当转动转盘的次数很大时,频率将会接近0.7.
(3)获得圆珠笔的概率约是0.7.
稳定性
稳定值
归纳总结
频率估计概率的一般步骤:
①大量重复试验;
②检验频率是否已表现出_______;
③频率的________即为概率.
1.用频率估计概率,可以发现,抛掷硬币“正面朝上”的概率为0.5是指( )
A.连续掷2次,结果一定是“正面朝上”和 “反面朝上”各1次
B.连续抛掷100次,结果一定是“正面朝上”和“反面朝上”各50次
C.抛掷2n次硬币,恰好有n次“正面朝上”
D.抛掷n次,当n越来越大时,正面朝上的频率会越来越稳定于0.5
D
随堂演练
2.在一个不透明的布袋中,红球、黑球、白球有若干个,除颜色外,形状、大小、质地等完全相同,小新从布袋中随机摸出一个球,记下颜色后放回布袋中,摇匀后再随机摸出一个球,记下颜色如此大量摸球试验后,小新发现其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%,对此试验,他总结出下列结论:
①若进行大量摸球试验,摸出白球的频率稳定于30%;
②若从布袋中任意摸出一个球,该球是黑球的概率最大;
③若再摸球100次,必有20次摸出的是红球.
其中说法正确的是( )
A.①②③ B.①② C.①③ D.②③
B
3.在一个不透明的盒子里装有除颜色不同其余均相同的黑、白两种球,其中白球24个,黑球若干.小兵将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球次数m 65 124 178 302 481 599 1803
摸到白球概率 0.65 0.62 0.593 0.604 0.601 0.599 0.601
(1)请估计:当n很大时,摸到白球的频率将会接近
(精确到0.1);
(2)假如你摸一次,估计你摸到白球的概率
P(白球)= .
0.6
0.6
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球次数m 65 124 178 302 481 599 1803
摸到白球概率 0.65 0.62 0.593 0.604 0.601 0.599 0.601
4.抛掷硬币“正面向上”的概率是0.5.如果连续抛掷100次,而结果并不一定是出现“正面向上”和“反面向上”各50次,这是为什么?
答:这是因为频数和频率的随机性以及一定的规律性.或者说概率是针对大量重复试验而言的,大量重复试验反映的规律并非在每一次试验中都发生.
5.某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题:
(1)这种树苗成活的频率稳定在_______,成活的概率估计值为______;
0.9
0.9
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活万棵;
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?
∴还需移植这种树苗约15万棵.
解:①估计这种树苗成活4.5万棵
②设还需植x万棵,依题意得
∴x=15,
(x+5)×0.9=18,
用频率估计概率
频率和概率的关系
步骤
频率是概率的近似值,概率是频率的稳定值.
①大量重复试验;
②检验频率是否已表现出稳定性;
③频率的稳定值即为概率.
课堂小结
第三十一章 随机事件的概率
31.3 第2课时 用频率估计概率
概率:一个数P(A)表示随机事件A发生的可能性大小, 称P(A)为事件A的概率.
P(A)=
频率:每个考察对象出现的次数与总次数的比值称为频率.
知识回顾
欣赏著名球星詹姆斯图片,你知道詹姆斯罚球命中率是多少吗
当试验的所有结果不是有限个,或各种可能结果发生的可能性不相等时,又该如何求事件发生的概率呢
情景导入
试验者 抛掷次数n “正面向上”次数m “正面向上”
频率( )
棣莫弗 2048 1061 0.518
布 丰 4040 2048 0.5069
费 勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮 尔 24000 12012 0.5005
历史上,有些人曾做过成千上万次抛掷硬币的试
验,其中一些试验结果见下表:
获取新知
通过大量重复试验,我们发现随着试验次数的增加,事件发生的频率逐渐稳定在常数0.5附近.
根据表中数据,描出对应的点,如图:
频率逐渐稳定
事件发生的概率
数学史实
人们在长期的实践中发现,在随机试验中,由于众多微小的偶然因素的影响,每次测得的结果虽不尽相同,但大量重复试验所得结果却能反应客观规律.这称为大数法则,亦称大数定律.
频率稳定性定理
思考 抛掷硬币试验的特点:
1.可能出现的结果数__________;
2.每种可能结果的可能性__________.
相等
有限
问题 如果某一随机事件,可能出现的结果是无限个,或
每种可能结果发生的可能性不一致,那么我们无法用列
举法求其概率,这时我们能够用频率来估计概率吗?
一起探究
从一定高度落下的图钉,着地时会有哪些可能的结果?
其中顶帽着地的可能性大吗?
做做试验来解决这个问题.
图钉落地的试验
试验探究
试验累计次数 20 40 60 80 100 120 140 160 180 200
钉帽着地的次数(频数) 9 19 36 50 61 68 77 84 95 109
钉帽着地的频率( %) 45 47.5 60 62.5 61 57 55 52.5 53 54.5
试验累计次数 220 240 260 280 300 320 340 360 380 400
钉帽着地的次数(频数) 122 135 143 155 162 177 194 203 215 224
钉帽着地的频率(%) 55 56.25 55 55 54 55 57 56.4 56.6 56
(1)选取20名同学,每位学生依次使图钉从高处落下20次,并根据试验结果填写下表.
56%
(%)
(2)根据上表画出统计图表示“顶帽着地”的频率.
(3)这个试验说明了什么问题.
在图钉落地试验中,“顶帽着地”的频率随着试验次数的增加,稳定在常数56%附近.
一般地,在大量重复试验中,随机事件A发生的频率 (这里n是实验总次数,它必须相当大,m是在n次试验中随机事件A发生的次数)会稳定到某个常数P.于是,我们用P这个常数表示事件A发生的概率,即P(A)=P.
归纳总结
则这个厂生产的瓷砖是合格品的概率估计值是______.(精确到0.01)
0.95
提示:运用频率和概率之间的关系,根据频率的波动情况估算概率.
例1 某瓷砖厂在相同条件下抽取部分瓷砖做耐磨试验,结果如下表所示:
例题讲解
例2 十一期间,某商场举行促销活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物20元以上就能获一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据:
转动转盘的次数 100 150 200 500 800 1 000
落在“圆珠笔”区域的次数 68 111 136 345 564 701
落在“圆珠笔”区域的频率
(1)计算并完成表格;
(2)请估计,当转动转盘的次数很大时,频率将会接近多少?
(3)假如你去转动该转盘一次,你获得圆珠笔的概率约是多少?
用落在“圆珠笔”区域的次数除以转动转盘的次数即是落在“圆珠笔”区域的频率,然后观察这组数趋向于哪个数,根据频率与概率的关系得出所求概率的值.
分析:
(1)
解:
转动转盘的次数 100 150 200 500 800 1 000
落在“圆珠笔”区域的次数 68 111 136 345 564 701
落在“圆珠笔”区域的频率 0.68 0.74 0.68 0.69 0.705 0.701
(2)当转动转盘的次数很大时,频率将会接近0.7.
(3)获得圆珠笔的概率约是0.7.
稳定性
稳定值
归纳总结
频率估计概率的一般步骤:
①大量重复试验;
②检验频率是否已表现出_______;
③频率的________即为概率.
1.用频率估计概率,可以发现,抛掷硬币“正面朝上”的概率为0.5是指( )
A.连续掷2次,结果一定是“正面朝上”和 “反面朝上”各1次
B.连续抛掷100次,结果一定是“正面朝上”和“反面朝上”各50次
C.抛掷2n次硬币,恰好有n次“正面朝上”
D.抛掷n次,当n越来越大时,正面朝上的频率会越来越稳定于0.5
D
随堂演练
2.在一个不透明的布袋中,红球、黑球、白球有若干个,除颜色外,形状、大小、质地等完全相同,小新从布袋中随机摸出一个球,记下颜色后放回布袋中,摇匀后再随机摸出一个球,记下颜色如此大量摸球试验后,小新发现其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%,对此试验,他总结出下列结论:
①若进行大量摸球试验,摸出白球的频率稳定于30%;
②若从布袋中任意摸出一个球,该球是黑球的概率最大;
③若再摸球100次,必有20次摸出的是红球.
其中说法正确的是( )
A.①②③ B.①② C.①③ D.②③
B
3.在一个不透明的盒子里装有除颜色不同其余均相同的黑、白两种球,其中白球24个,黑球若干.小兵将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球次数m 65 124 178 302 481 599 1803
摸到白球概率 0.65 0.62 0.593 0.604 0.601 0.599 0.601
(1)请估计:当n很大时,摸到白球的频率将会接近
(精确到0.1);
(2)假如你摸一次,估计你摸到白球的概率
P(白球)= .
0.6
0.6
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球次数m 65 124 178 302 481 599 1803
摸到白球概率 0.65 0.62 0.593 0.604 0.601 0.599 0.601
4.抛掷硬币“正面向上”的概率是0.5.如果连续抛掷100次,而结果并不一定是出现“正面向上”和“反面向上”各50次,这是为什么?
答:这是因为频数和频率的随机性以及一定的规律性.或者说概率是针对大量重复试验而言的,大量重复试验反映的规律并非在每一次试验中都发生.
5.某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题:
(1)这种树苗成活的频率稳定在_______,成活的概率估计值为______;
0.9
0.9
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活万棵;
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?
∴还需移植这种树苗约15万棵.
解:①估计这种树苗成活4.5万棵
②设还需植x万棵,依题意得
∴x=15,
(x+5)×0.9=18,
用频率估计概率
频率和概率的关系
步骤
频率是概率的近似值,概率是频率的稳定值.
①大量重复试验;
②检验频率是否已表现出稳定性;
③频率的稳定值即为概率.
课堂小结
