冀教版数学九年级下册同步课件:31.3 第1课时 频率的稳定性(共17张PPT)
文档属性
| 名称 | 冀教版数学九年级下册同步课件:31.3 第1课时 频率的稳定性(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 411.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-28 13:46:18 | ||
图片预览






文档简介
(共17张PPT)
第三十一章 随机事件的概率
31.3 第1课时 频率的稳定性
情景导入
掷一枚硬币,正面向上的概率应该是0.5,但小明做了10次试验,正面向上的次数只有3次,这是为什么呢?
问题1 抛掷一枚均匀硬币,硬币落地后,会出现哪些可能的结果呢?
问题2 它们的概率是多少呢?
出现“正面朝上”和“反面朝上”两种情况
都是
问题3 在实际掷硬币时,会出现什么情况呢?
获取新知
一起探究
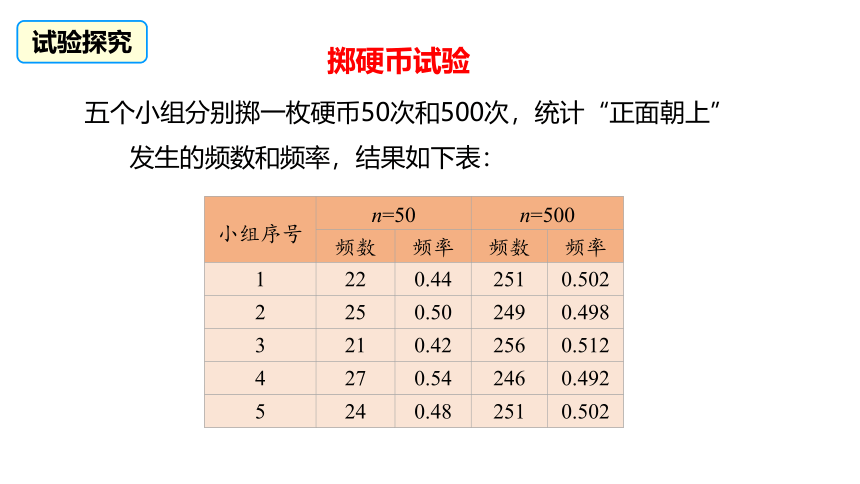
五个小组分别掷一枚硬币50次和500次,统计“正面朝上”发生的频数和频率,结果如下表:
小组序号 n=50 n=500 频数 频率 频数 频率
1 22 0.44 251 0.502
2 25 0.50 249 0.498
3 21 0.42 256 0.512
4 27 0.54 246 0.492
5 24 0.48 251 0.502
试验探究
掷硬币试验
将上面的试验结果用折线统计图表示,如图所示.
想一想:1.当实验次数较小时,频率有什么特征?
2.当实验次数很大时,频率有什么样的变化趋势?
1. 当实验次数较小时,频率不稳定,波动较大.
2. 当实验次数很大时,频率的波动减小.
归 纳
思 考
试验者 抛掷次数n “正面向上”次数m “正面向上”
频率( )
棣莫弗 2048 1061 0.518
布 丰 4040 2048 0.5069
费 勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮 尔 24000 12012 0.5005
分析下面数学家大量重复试验数据,结合前面自己的试验数据,你有何发现?
试验次数越多频率越接近0.5
1.对掷硬币试验,“正面朝上”的概率为0.5,而频率则具有不确定性.
2.试验次数不同,频率可能不同;即使是相同次数的不同试验,频率也可能不同.
3.当试验次数较小时,频率的波动较大,但是随着试验次数的增大,“正面朝上”发生的频率波动明显减小,逐渐稳定到0.5附近.这个性质叫做频率的稳定性.
这个数值是什么?
归 纳
一位同学在“抛硬币”游戏中获得的数据如下表:
抛掷次数 10 15 20 25
出现正面朝上的频数 4 7 8 9
出现正面朝上的频率 40% 46.7% 40% 36%
针对训练
由此他得出结论:随着抛掷次数的增加,出现正面朝上的频率逐渐稳定在40%附近,你认为该同学的判断正确吗?
本题中的试验次数较少,应该多做一些试验,待事件出现的频率逐渐稳定到某一个数值,我们就可以用平稳时的频率去估计这一事件在每次抛掷时发生的可能性的大小.
分析:
该同学的判断不正确.
解:
总 结
频率的稳定性的前提是在试验次数足够多的情况下,对不同次数的试验,事件的频率可能不同.当试验次数较少时,看不出什么规律,但当试验次数足够多时,频率逐渐稳定到某一个数值.
例 下表是某批足球质量检验获得的数据,请根据此表回答,当抽取的足球数很大时,这批足球优等品的频率会在常数_________附近摆动.
抽取的足球数 50 100 200 500 1000 2000
优等品数 47 95 194 472 953 1902
0.95
例题讲解
频数= ≈0.95.
即这批足球优等品的频率会在常数0.95附近摆动.
解析:
1.某种彩票的中奖机会是1%,下列说法正确的是( )
A.买1张这种彩票一定不会中奖
B.买1张这种彩票一定会中奖
C.买100张这种彩票一定会中奖
D.当购买彩票的数量很大时,中奖的频率稳定
在1%附近
D
随堂演练
2.某人在做掷硬币试验时,投掷m次,正面朝上有n次(即正面朝上的频率P= ),则下列说法正确的是( )
A. P一定等于
B. P一定不等于
C.多投掷一次, P更接近
D.随着投掷次数的逐渐增加, P稳定在 附近
D
3.为了看图钉落地后钉尖着地的频率有多大,小明做了大量重复试验,发现钉尖着地的次数是试验总次数的40%,下列说法错误的是( )
A.钉尖着地的频率是0.4
B.随着试验次数的增加,钉尖着地的频率逐渐稳定
在某一个常数附近
C.前10次试验结束后,钉尖着地的次数一定是4次
D.前10次试验结束后,钉尖着地的次数不一定是4次
C
4.某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息,这种树苗成活的频率稳定在_______.
0.9
课堂小结
大量重复试验
频率稳定
常数附近
统计思想
第三十一章 随机事件的概率
31.3 第1课时 频率的稳定性
情景导入
掷一枚硬币,正面向上的概率应该是0.5,但小明做了10次试验,正面向上的次数只有3次,这是为什么呢?
问题1 抛掷一枚均匀硬币,硬币落地后,会出现哪些可能的结果呢?
问题2 它们的概率是多少呢?
出现“正面朝上”和“反面朝上”两种情况
都是
问题3 在实际掷硬币时,会出现什么情况呢?
获取新知
一起探究
五个小组分别掷一枚硬币50次和500次,统计“正面朝上”发生的频数和频率,结果如下表:
小组序号 n=50 n=500 频数 频率 频数 频率
1 22 0.44 251 0.502
2 25 0.50 249 0.498
3 21 0.42 256 0.512
4 27 0.54 246 0.492
5 24 0.48 251 0.502
试验探究
掷硬币试验
将上面的试验结果用折线统计图表示,如图所示.
想一想:1.当实验次数较小时,频率有什么特征?
2.当实验次数很大时,频率有什么样的变化趋势?
1. 当实验次数较小时,频率不稳定,波动较大.
2. 当实验次数很大时,频率的波动减小.
归 纳
思 考
试验者 抛掷次数n “正面向上”次数m “正面向上”
频率( )
棣莫弗 2048 1061 0.518
布 丰 4040 2048 0.5069
费 勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮 尔 24000 12012 0.5005
分析下面数学家大量重复试验数据,结合前面自己的试验数据,你有何发现?
试验次数越多频率越接近0.5
1.对掷硬币试验,“正面朝上”的概率为0.5,而频率则具有不确定性.
2.试验次数不同,频率可能不同;即使是相同次数的不同试验,频率也可能不同.
3.当试验次数较小时,频率的波动较大,但是随着试验次数的增大,“正面朝上”发生的频率波动明显减小,逐渐稳定到0.5附近.这个性质叫做频率的稳定性.
这个数值是什么?
归 纳
一位同学在“抛硬币”游戏中获得的数据如下表:
抛掷次数 10 15 20 25
出现正面朝上的频数 4 7 8 9
出现正面朝上的频率 40% 46.7% 40% 36%
针对训练
由此他得出结论:随着抛掷次数的增加,出现正面朝上的频率逐渐稳定在40%附近,你认为该同学的判断正确吗?
本题中的试验次数较少,应该多做一些试验,待事件出现的频率逐渐稳定到某一个数值,我们就可以用平稳时的频率去估计这一事件在每次抛掷时发生的可能性的大小.
分析:
该同学的判断不正确.
解:
总 结
频率的稳定性的前提是在试验次数足够多的情况下,对不同次数的试验,事件的频率可能不同.当试验次数较少时,看不出什么规律,但当试验次数足够多时,频率逐渐稳定到某一个数值.
例 下表是某批足球质量检验获得的数据,请根据此表回答,当抽取的足球数很大时,这批足球优等品的频率会在常数_________附近摆动.
抽取的足球数 50 100 200 500 1000 2000
优等品数 47 95 194 472 953 1902
0.95
例题讲解
频数= ≈0.95.
即这批足球优等品的频率会在常数0.95附近摆动.
解析:
1.某种彩票的中奖机会是1%,下列说法正确的是( )
A.买1张这种彩票一定不会中奖
B.买1张这种彩票一定会中奖
C.买100张这种彩票一定会中奖
D.当购买彩票的数量很大时,中奖的频率稳定
在1%附近
D
随堂演练
2.某人在做掷硬币试验时,投掷m次,正面朝上有n次(即正面朝上的频率P= ),则下列说法正确的是( )
A. P一定等于
B. P一定不等于
C.多投掷一次, P更接近
D.随着投掷次数的逐渐增加, P稳定在 附近
D
3.为了看图钉落地后钉尖着地的频率有多大,小明做了大量重复试验,发现钉尖着地的次数是试验总次数的40%,下列说法错误的是( )
A.钉尖着地的频率是0.4
B.随着试验次数的增加,钉尖着地的频率逐渐稳定
在某一个常数附近
C.前10次试验结束后,钉尖着地的次数一定是4次
D.前10次试验结束后,钉尖着地的次数不一定是4次
C
4.某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息,这种树苗成活的频率稳定在_______.
0.9
课堂小结
大量重复试验
频率稳定
常数附近
统计思想
